Файл: Тема Задачи исследования операций с целочисленными переменными.doc
Добавлен: 09.11.2023
Просмотров: 82
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
x6 входит со знаком минус, введем в него базисную искусственную переменную x6 ≥ 0 и решим следующую M-задачу.
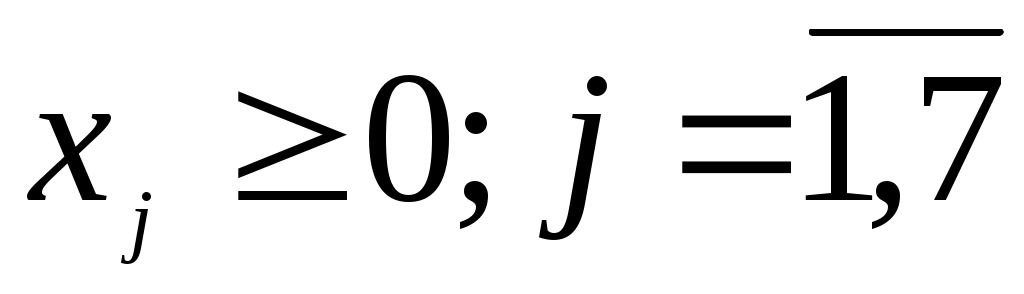
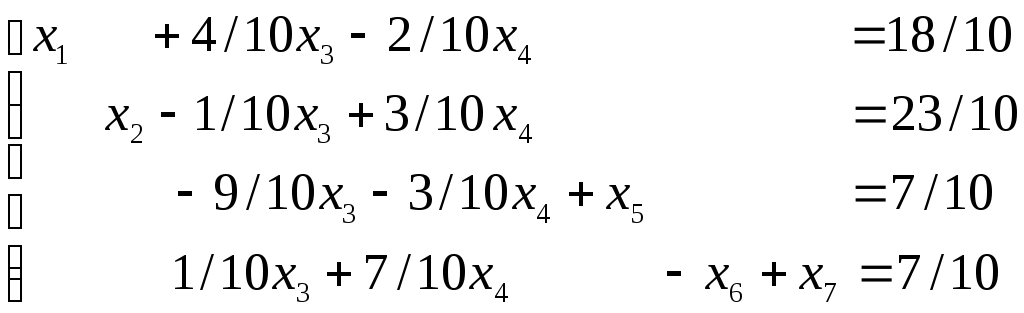(4.8)
T = 4x1 + 5x2 + 0∙x3 + 0∙x4 + 0∙x5 + 0∙x6 – Mx7→ max
Оптимальное решение M-задачи: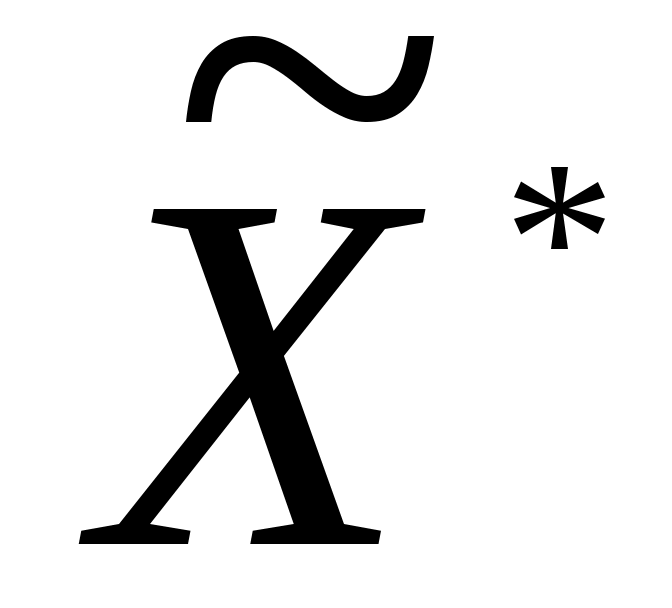
=(2, 2, 0, 1, 1, 0, 0);
Tmax =T(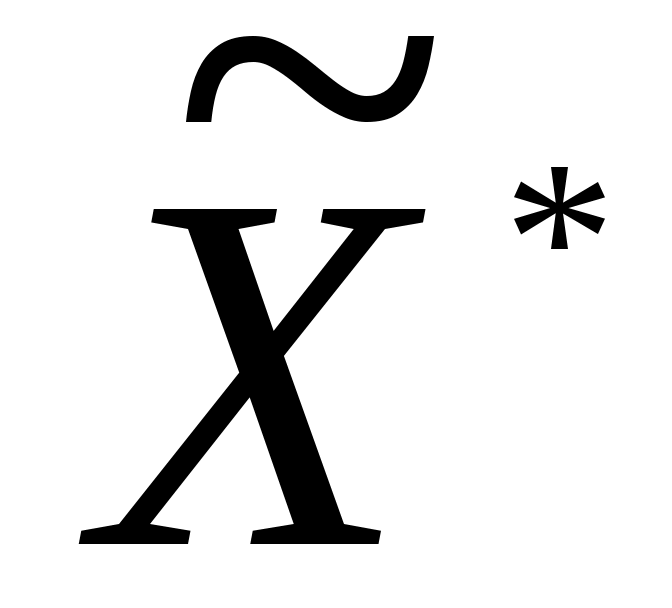 ) = 18.
Искусственная переменная x7 = 0, поэтому оптимальным решением задачи (4.7) будет соответствующее решение:
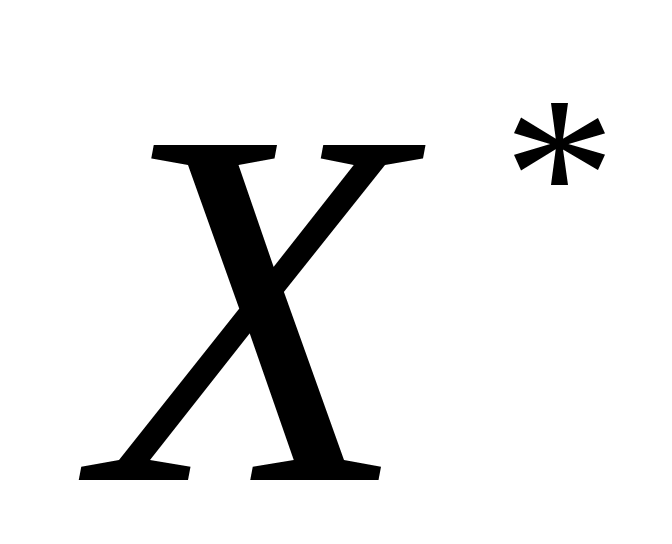=(2, 2, 0, 1, 1, 0); Zmax = Tmax = 18.
Значения всех переменных целочисленные, поэтому оптимальное целочисленное решение исходной З.Л.Ц.П.:
= (2;2); Zmax = 18.
Задачу (4.6) можно решить двойственным симплекс-методом. Для этого 4-е уравнение умножим на «–1» (левую и правую части), уравнение будет иметь базисную переменную x6, но исходное решение системы уравнений полученной задачи будет базисным, но не опорным. Это уравнение: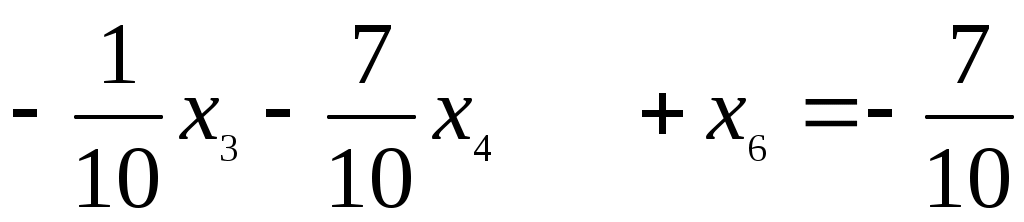
введем непосредственно в последнюю оптимальную симплекс-таблицу решения исходной З.Л.П., добавив к ней столбец и строку соответствующие переменной x6. исходная таблица будет иметь вид.
Исходное базисное, но не опорное решение выписываем из этой таблицы: X0 = (18/10, 23/10, 0,0,7/10,-7/10)
Двойственный симплекс-метод устраняет отрицательность в свободных членах bi и сохраняет неотрицательность оценок в Z-строке.
Правила двойственного симплекс-метода.
В качестве разрешающей строка r выбираем строку с bi< 0. Если таких строк несколько выбираем любую из них. Разрешающий столбец выбираем по правилу:
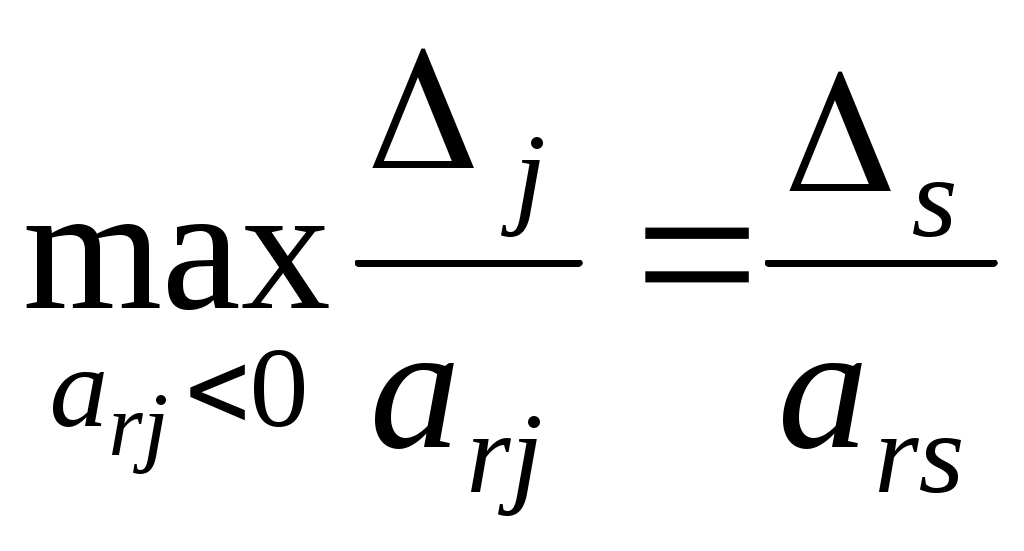, т.е.
элементы Z-строки делим на соответствующие отрицательные элементы разрешающей строки r и из этих отношений выбираем максимальное.
Столбец s, соответствующей максимальному отношению будет разрешающим, а элемент ars – разрешающим элементом.
В рассмотренном примере, в таблице строка соответствующая отрицательному свободному члену: – 7/10 будет разрешающей.
Находим разрешающий элемент:
.
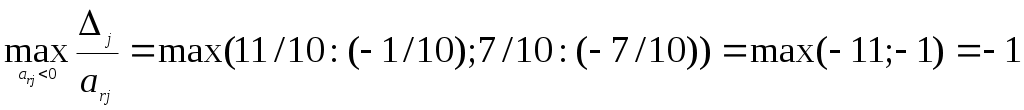Разрешающий элемент: –7/10. Отметим его в таблице и выполним одно полное исключение неизвестной, одну итерацию, получим следующую таблицу, отличающуюся от оптимальной таблицы решения M-задачи только столбцом x7. Из нее выписываем ранее полученное решение.
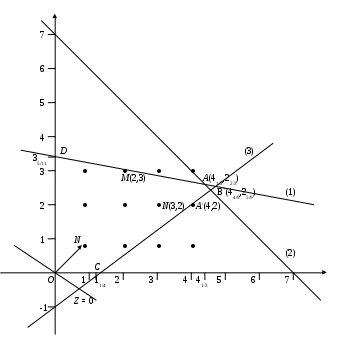
Рис. 1
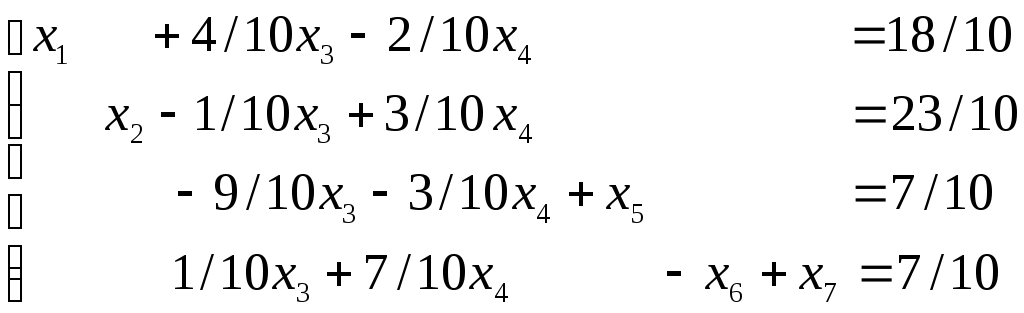(4.8)T = 4x1 + 5x2 + 0∙x3 + 0∙x4 + 0∙x5 + 0∙x6 – Mx7→ max
 Cj | 4 | 5 | 0 | 0 | 0 | 0 | –M | bi |  | |
| Ci | xj xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 | ||
| 4 | x1 | 1 | 0 | 4/10 | -2/10 | 0 | 0 | 0 | 18/10 | ― |
| 5 | x2 | 0 | 1 | -1/10 | 3/10 | 0 | 0 | 0 | 23/10 | 23/10:3/10=23/3 |
| 0 | x5 | 0 | 0 | -9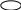/10 | -  3/10 | 1 | 0 | 0 | 7/10 | ― |
| -M | X7 | 0 | 0 | 1/10 | 7/10 | 0 | -1 | 1 | 7/10 | 7/10:7/10=1min |
| T | 0 | 0 | -1/10M+11/10 | -7/10M+7/10↑ | 0 | M | 0 | -7/10M+187/10 | | |
| 4 | x1 | 1 | 0 | 3/7 | 0 | 0 | -2/7 | 2/7 | 2 | |
| 5 | x2 | 0 | 1 | -1/7 | 0 | 0 | 3/7 | -3/7 | 2 | |
| 0 | x5 | 0 | 0 | -6/7 | 0 | 1 | -3/7 | 3/7 | 1 | |
| 0 | x4 | 0 | 0 | 1/7 | 1 | 0 | -10/7 | 10/7 | 1 | |
| T | 0 | 0 | 1 | 0 | 0 | 1 | M-1 | 18 | | |
Оптимальное решение M-задачи:
=(2, 2, 0, 1, 1, 0, 0); Tmax =T(
) = 18.Искусственная переменная x7 = 0, поэтому оптимальным решением задачи (4.7) будет соответствующее решение:
=(2, 2, 0, 1, 1, 0); Zmax = Tmax = 18.Значения всех переменных целочисленные, поэтому оптимальное целочисленное решение исходной З.Л.Ц.П.:
= (2;2); Zmax = 18.Задачу (4.6) можно решить двойственным симплекс-методом. Для этого 4-е уравнение умножим на «–1» (левую и правую части), уравнение будет иметь базисную переменную x6, но исходное решение системы уравнений полученной задачи будет базисным, но не опорным. Это уравнение:
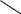введем непосредственно в последнюю оптимальную симплекс-таблицу решения исходной З.Л.П., добавив к ней столбец и строку соответствующие переменной x6. исходная таблица будет иметь вид.| C  j | 4 | 5 | 0 | 0 | 0 | 0 | bi | |
| Ci | xj xi | x1 | x2 | x3 | x4 | x5 | x6 | |
| 4 | x1 | 1 | 0 | 4/10 | -2/10 | 0 | 0 | 18/10 |
| 5 | x2 | 0 | 1 | -1/10 | 3/10 | 0 | 0 | 23/10 |
| 0 | x5 | 0 | 0 | -9/10 | -3/10 | 1 | 0 | 7/10 |
| 0 | x6 | 0 | 0 | -1/10 | -  7/10 | 0 | 1 | -7/10 |
| Z | 0 | 0 | 11/10 | 7/10 | 0 | 0 | 187/10 | |
Исходное базисное, но не опорное решение выписываем из этой таблицы: X0 = (18/10, 23/10, 0,0,7/10,-7/10)
Двойственный симплекс-метод устраняет отрицательность в свободных членах bi и сохраняет неотрицательность оценок в Z-строке.
Правила двойственного симплекс-метода.
В качестве разрешающей строка r выбираем строку с bi< 0. Если таких строк несколько выбираем любую из них. Разрешающий столбец выбираем по правилу:
, т.е.элементы Z-строки делим на соответствующие отрицательные элементы разрешающей строки r и из этих отношений выбираем максимальное.
Столбец s, соответствующей максимальному отношению будет разрешающим, а элемент ars – разрешающим элементом.
В рассмотренном примере, в таблице строка соответствующая отрицательному свободному члену: – 7/10 будет разрешающей.
Находим разрешающий элемент:
.Разрешающий элемент: –7/10. Отметим его в таблице и выполним одно полное исключение неизвестной, одну итерацию, получим следующую таблицу, отличающуюся от оптимальной таблицы решения M-задачи только столбцом x7. Из нее выписываем ранее полученное решение.
| C  j | 4 | 5 | 0 | 0 | 0 | 0 | bi | |
| Ci | xj xi | x1 | x2 | x3 | x4 | x5 | x6 | |
| 4 | x1 | 1 | 0 | 3/7 | 0 | 0 | -2/7 | 2 |
| 5 | x2 | 0 | 1 | -1/7 | 0 | 0 | 3/7 | 2 |
| 0 | x5 | 0 | 0 | -6/7 | 0 | 1 | -3/7 | 1 |
| 0 | x4 | 0 | 0 | 1/7 | 1 | 0 | -10/7 | 1 |
| Z | 0 | 0 | 1 | 0 | 0 | 1 | 18 | |
Рис. 1