Файл: Тема Задачи исследования операций с целочисленными переменными.doc
Добавлен: 09.11.2023
Просмотров: 81
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
§3. Общая характеристика методов отсечения
Рассмотри задачу линейного целочисленного программирования (З.Л.Ц.П.):
xj ≥ 0,
xj –целые,
где aij и bi (
Пусть условия (3.2) , (3.3) определяют некоторый многогранник D1, а условия (3.2) – (3.4) – множество Dц целочисленных точек решений исходной З.Л.Ц.П.
Для решения этой задачи можно использовать методы отсечения. Идея этих методов впервые была опубликована в работах американских математиков Данцига, Фалкерсона и Джонсона. Для задач целочисленного программирования эта идея впервые была описана Данцигом. Она заключается в следующем.
Пусть нам удалось построить выпуклую оболочку
Dk получается отсечением от многогранника Dk-1 некоторой его части, не содержащей целочисленных точек. Отсечение осуществляется введением дополнительного ограничения. Это ограничение обладает двумя свойствами:
-
ему удовлетворяют все целочисленные решения исходного З.Л.Ц.П. -
оптимальное нецелочисленное решение З.Л.П. не удовлетворяет этому ограничению.
Такое ограничение называется правильным отсечением.
На основе этой идеи американский математик Гомори предложил алгоритм решения задач целочисленного программирования, он обосновал правила построения дополнительных ограничений, т.е. многогранников Dk и доказал сходимость алгоритма.
§4. Алгоритм Гомори.
Первый шаг. Решим задачу максимизации функции Z на многограннике D1, т.е. задачу линейного программирования. (3.1) – (3.3) симплексным методом, предварительно приведя ее к стандартному виду. Через конечное число шагов получим оптимальную таблицу:
| СП БП | x1 | x2 | … | xn | xn+1 | xn+2 | … | xn+m | bi |
| xi1 | | | … | | | | … | | |
| xi2 | | | … | | | | … | | |
| … | … | … | … | … | … | … | … | … | … |
| xim | | | … | | | | … | | |
| Z | q1 | q2 | … | qn | qn+1 | qn+2 | … | qn+m | Q |
где xi1, xi2, …, xim – базисные переменные множества всех переменных {x1, x2, …,xn+m}. В этой таблице: qj ≥ 0,
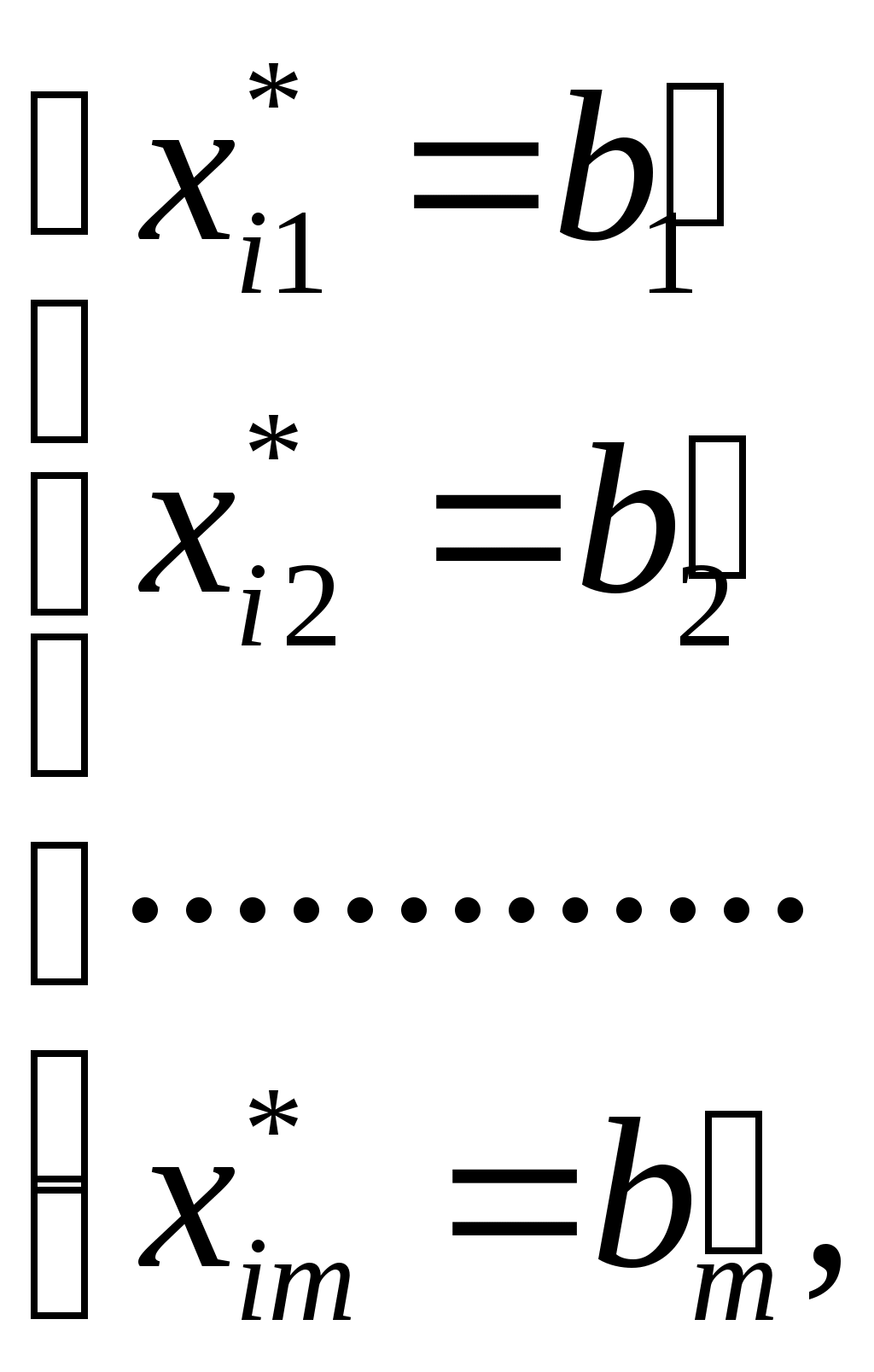 (4.1),
(4.1),а свободные переменные равны нулю. Эти условия определяют оптимальное решение задачи (3.1) – (3.3), точку многогранника D(1). Если все
Если среди значений
Второй шаг. Построение дополнительного ограничения – правильного сечения.
Пусть
где
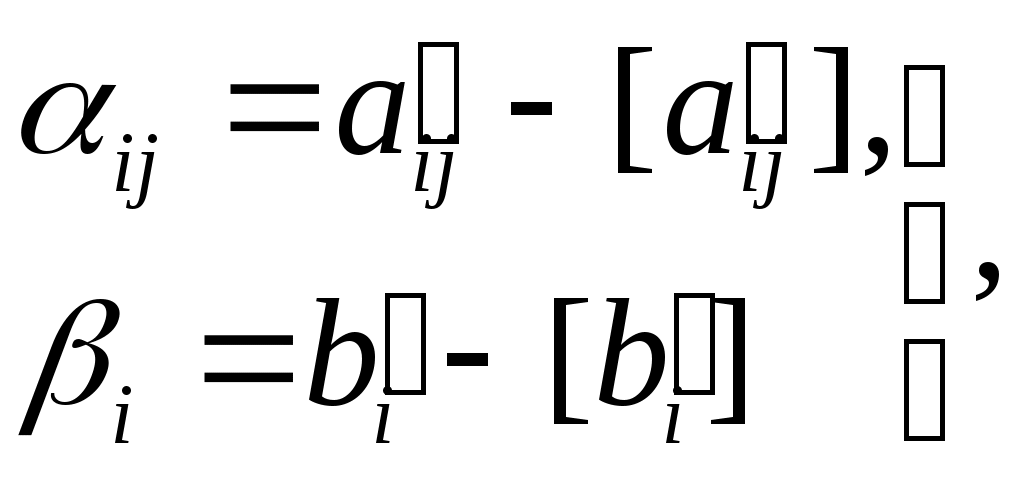 (4.3)
(4.3)где
Так как все
Третий шаг. Ограничение (4.2) добавляем к системе (3.2), (3.3) и решаем новую З.Л.П.
xj≥ 0,
(3.3)
Условия (3.2), (3.3), (4.2) определяют многогранник D2,которому принадлежат все целочисленные точки области D1, но не принадлежит оптимальная нецелочисленная точка многогранника D1.
Решаем задачу (3.1) – (3.3), (4.2) М-методом. Если полученное при этом оптимальное решение будет целочисленным, то оно и будет оптимальным решением исходной З.Л.Ц.П., если нет, то повторяем второй и третий шаги до тех пор, пока не будет получено оптимальное целочисленное решение, либо мы убедимся в неразрешимости задачи (3.1) – (3.4).
Если в симплексной таблице появится строка с нецелочисленным свободным членом, а остальные элементы этой – целые числа, то это означает, что соответствующее уравнение не имеет целочисленного решения и исходная З.Л.Ц.П. неразрешима.
Замечания:
-
При решении каждой новой З.Л.П. ограничение типа (4.2) приведенное к эквивалентному уравнению можно вводить непосредственно в оптимальную таблицу решения предыдущей задачи. -
Студенты изучившие тему «Двойственный симплекс-метод», могут применять его для решения задач построенных на третьем шаге.
Пример.
Решить З.Л.Ц.П. методом Гомори.
Z = 4x1 + 5x2 → max
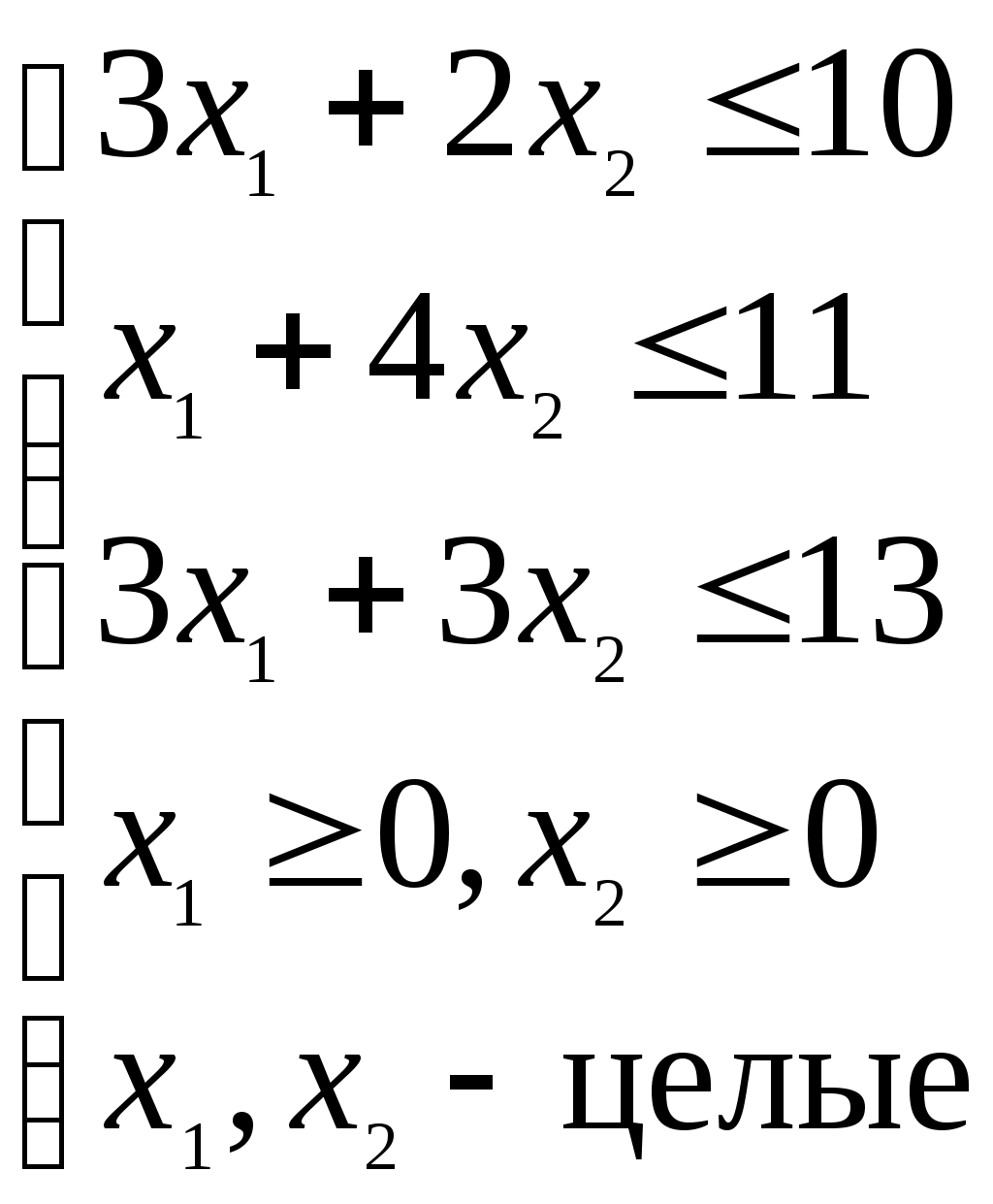
1-й шаг. Приведем к стандартному виду исходную З.Л.П. и решим ее симплекс-методом.
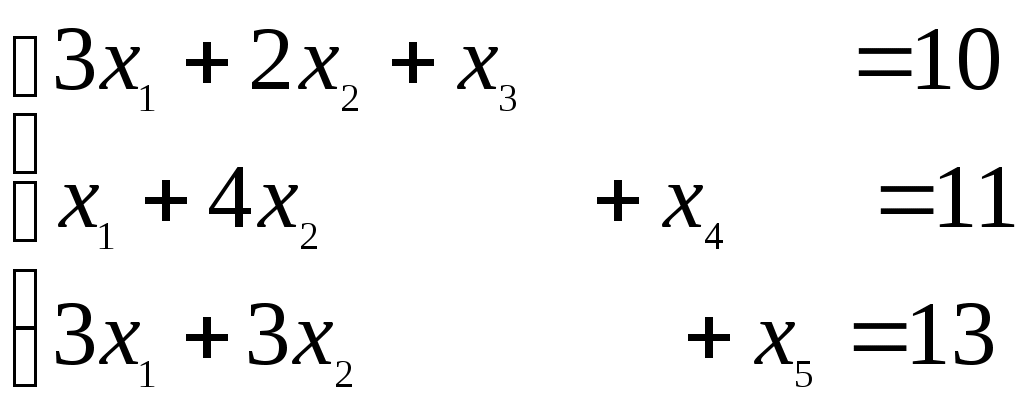 (4.4)
(4.4)Z = 4x1 + 5x2 + 0∙x3 + 0∙x4 + 0∙x5 → max

| Cj | 4 | 5 | 0 | 0 | 0 | bi | | |
| Ci | xj xi | x1 | x2 | x3 | x4 | x5 | ||
| 0 | x3 | 3 | 2 | 1 | 0 | 0 | 10 | 10/2 |
| 0 | x4 | 1 | 4  | 0 | 1 | 0 | 11 | 11/4 min |
| 0 | x5 | 3 | 3 | 0 | 0 | 1 | 13 | 13/3 |
| Z | -  4 4 | -5↑ | 0 | 0 | 0 | 0 | | |
| 0 | x3 | 10/4 | 0 | 1 | -2/4 | 0 | 18/4 | 18/4:10/4=18/10 min |
| 5 | x2 | 1/4 | 1 | 0 | 1/4 | 0 | 11/4 | 11/4:1/4=11 |
| 0 | x5 | 9/4 | 0 | 0 | -3/4 | 1 | 19/4 | 19/4:9/4=19/9 |
| Z | -11/4↑ | 0 | 0 | 5/4 | 0 | 55/4 | | |
| 4 | x1 | 1 | 0 | 4/10 | -2/10 | 0 | 18/10 | |
| 5 | x2 | 0 | 1 | -1/10 | 3/10 | 0 | 23/10 | |
| 0 | x5 | 0 | 0 | -9/10 | -3/10 | 1 | 7/10 | |
| Z | 0 | 0 | 11/10 | 7/10 | 0 | 187/10 | | |
Оптимальное решение:
Решение нецелочисленное, переходим ко второму шагу.
2-ой шаг. Строим правильное отсечение по любой из строк, соответствующих нецелочисленной переменной, например по 3-й строке, соответствующей базисной переменной x3.
α31x1 + α32x2 + α33x3 + α34x4 + α35x5 ≥ β3.
В этом неравенстве α31, α32 и α35 равны нулю, они соответствуют значением
Новое ограничение имеет вид:
3-й шаг. Вводим это ограничение в систему ограничений исходной З.Л.П. (4.4) и полученную задачу приводим к стандартному виду. Неравенство (4.5) эквивалентно уравнению
Новая З.Л.П. имеет вид:
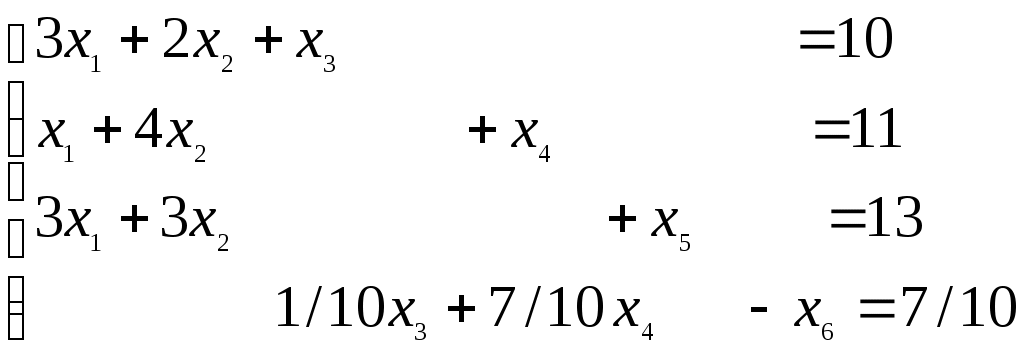 (4.6)
(4.6)Z = 4x1 + 5x2 + 0∙x3 + 0∙x4 + 0∙x5 + 0∙x6 → max
Первые 3 уравнения задачи эквивалентны уравнения приведенным к базисным переменным x1, x2, x5, которые выписываем из последней таблицы решения исходной З.Л.П.; с учетом этого задача (4.6) будет иметь вид:
 (4.7)
(4.7)Z = 4x1 + 5x2 + 0∙x3 + 0∙x4 + 0∙x5 + 0∙x6 → max
Так как в четвертом уравнении переменная