Файл: Тема Задачи исследования операций с целочисленными переменными.doc

Тема 1. Задачи исследования операций с целочисленными переменными

§ 1. Типы задач целочисленного программирования

В своей практической хозяйственной деятельности человек часто встречается с задачами, в которых переменные в силу их физического смысла могут принимать только целочисленные значения. К таким задачам относятся: задачи о раскрое, о размещении производства, о назначениях, о производстве неделимой продукции и многие другие.

При построении моделей таких задач надо вводить дополнительные условия целочисленности переменных. С таким дополнительным условием задачи исследований операций называются целочисленными. Изучением таких задач занимается целочисленное (дискретное) программирование. Если все остальные ограничения, кроме условия целочисленности являются линейными, то такие задачи называются задачами линейного целочисленного программирования (З.Л.Ц.П).

З.Л.Ц.П. бывают 2-х типов: задачи с неделимостями и задачи выбора вариантов или экстремальные комбинаторные задачи. В задачах с неделимостями переменные по-своему физическому смыслу не могут принимать дробные значения. Это задачи о выпуске неделимой продукции (автомобили, телевизоры и т.д.), о раскрое (количество деталей раскраиваемых тем или иным способом), задачи распределения станков по видам работ и т.д.

В задачах с неделимостями З.Л.Ц.П. формулируется также, как и соответствующая З.Л.П., но к системе ограничений добавляется требование целочисленности переменных. Если это требование накладывается на все переменные, то задача называется полностью целочисленной, если только на часть –частично целочисленной.

Второй тип задач – задачи выбора вариантов, часто встречаются в планировании и управлении. В задачах выбора переменные могут принимать только два значения: ноль или единица. Такие переменные называются булевыми переменными.

Одной из наиболее простых и первых задач такого типа – является задача о назначениях, сформулированная венгерским математиком Эгервари в 1932 г. Систематические исследования по целочисленному программированию начинаются с 1955 г. – когда на 2-м симпозиуме по математическому программированию была сформулирована задача о бомбардировщике, известная также, как задача о ранце.

---

§2. Модель целочисленных задач исследования операций.

Рассмотрим некоторые характерные задачи, требующие целочисленного решения. Некоторые задачи формально не являются целочисленными, но имеют целочисленные решения при любых целочисленных данных. К таким задачам относятся задачи сводящиеся к целочисленным. Рассмотрим постановку и математическую модель транспортной задачи.

Транспортная задача.

В пунктах A₁, A₂, . . . ,A_m сосредоточен некоторый однородный груз в количестве a₁, a₂,…,a_m соответственно. Этот груз надо вывести в пункты B₁, B₂,…, B_n в количестве b₁, b₂,…,b_n соответственно. Известна стоимость перевозки единицы груза из пункта A_i ( ) в пункт B_j ( ). Обозначим через x_ij ( ) количество груза, перевезенного из пункта A_i в пункт B_j. И пусть суммарные запасы грузов равны суммарным потребностям в них, т.е.

.

Необходимо найти такие значения перевозок:

x_ij ≥ 0, , (2.1)

которые удовлетворяют условиям

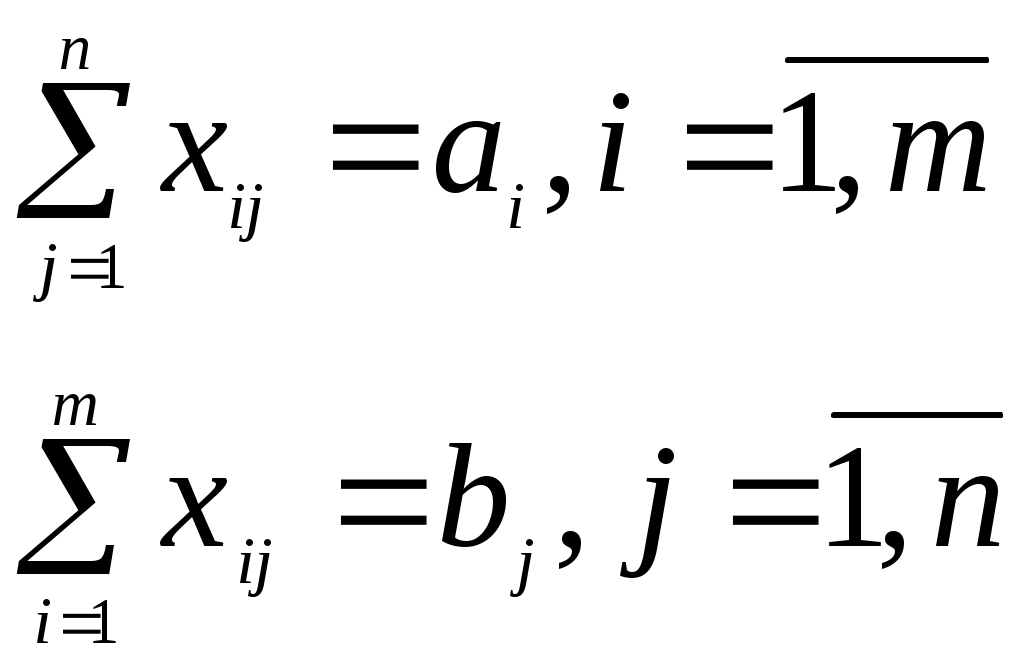(2.2)

и минимизируют общую стоимость транспортировки грузов, т.е.

(2.3)

Транспортная задача, т.е. задача (2.1) – (2.3) формально целочисленной не является, так мак на переменные задачи x_ij требование целочисленности не накладывается.

Заметим, что при любых целых значениях a₁, a₂,…,a_m и b₁, b₂,…,b_n транспортная задача всегда имеет целочисленный оптимальный план независимо от значений C_ij.

Действительно, решая задачу методом потенциалов замечаем, что

а) исходный опорный план является целочисленным

---

;

б) при переходе от одного опорного плана к другому целочисленность сохраняется. Отсюда и следует целочисленность оптимального плана.

Для всех задач, сводящихся к транспортной существует целочисленный оптимальный план, при условии, что a_i ( ) иb_j( ) являются целыми числами.

Задача о ранце. Для перевозки n видов неделимых предметов используется m видов ресурсов (транспортных средств), заданных в количестве b₁, b₂,…,b_m.

Известны:

цена одного предмета j-го вида: C_j , ; расход i-го ресурса для перевозки одного предмета j-го вида: .

Требуется определить сколько предметов каждого типа надо перевезти, чтобы суммарная стоимость ценность этих предметов была максимальной. Обозначим через x_j –количество выбранных для перевозки предметов j-го вида, . Математическая модель задачи запишется так:

Найти значения x_j, , которые удовлетворяют условиям:

x_j≥ 0, (2.4)

x_j – целые, (2.5)

(2.6)

и максимизируют функцию:

(2.7)

Условие (2.5) учитывает требование неделимости предметов, (2.6) – ограничения по ресурсам, (2.7) – выражает суммарную стоимость перевезенных предметов.

Частным случаем задачи (2.4) – (2.7) является задача, в которой любой из заданного набора предметов j = 1, 2, …, n, может быть выбран или нет. Переменные x_j могут принимать только два значения: 0 (предмет не выбирается) или 1 (предмет выбирается).

Математическая модель задачи запишется так:

Найти такие значения

---

x_j, , которые удовлетворяют условиям:

(2.8)

(2.9)

и максимизируют функцию

(2.10)

Задача (2.4) – (2.7) является задачей с неделимостями, а задача (2.8) – (2.10) – задачей выбора ( с булевыми переменными).
Задача о назначениях. Имеется nработ и n исполнителей. Известны затраты C_ij, на выполнение i-ым исполнителем j-ой работы. Требуется назначить каждого исполнителя на одну и только одну работу так, чтобы суммарные затраты были минимальными. Обозначим через x_ij переменные, равные единице, если i-ый исполнитель назначен на j-ю работы и нулю – в противном случае.

Математическая модель задачи:

Найти значения x_ij, удовлетворяющие условиям:

(2.11)
(2.12)

(2.13)

и минимизирующие функцию суммарных затрат, т.е.

(2.14)

Условие (2.12) означает, что каждому исполнителю будет представлена работа и только одна; условие (2.13) , что на каждую работу будет назначен исполнитель и притом только один.

Условия (2.11) вообще говоря, сильно усложняют решение задачи. Однако, для данной задачи эти условия можно заменить на более простые: x_ij ≥ 0, , . Это можно сделать, так как задачи (2.11) – (2.14) является частным случаем транспортной задачи, для которой всегда имеется целочисленное решение при целых величинах потребностей и запасов.

Особенности задач. В задачах целочисленного программирования область решений является невыпуклой и несвязной, поэтому решение таких задач связано с определенными трудностями. Казалось бы естественным решить вместо задачи целочисленного программирования соответствующую задачу линейного программирования, и если

---

компоненты решения окажутся нецелыми числами, то округлить их до ближайших целых чисел. Очень часто полученное таким способом решение не только не является оптимальным, но оказывается и недопустимым. Оптимум в таких задачах может находится как на границе, так и внутри области и решений соответствующей З.Л.П.

Убедимся в этом на следующем примере.

Пример.

x₁ ≥ 0, x₂ ≥ 0

x₁, x₂ – целые



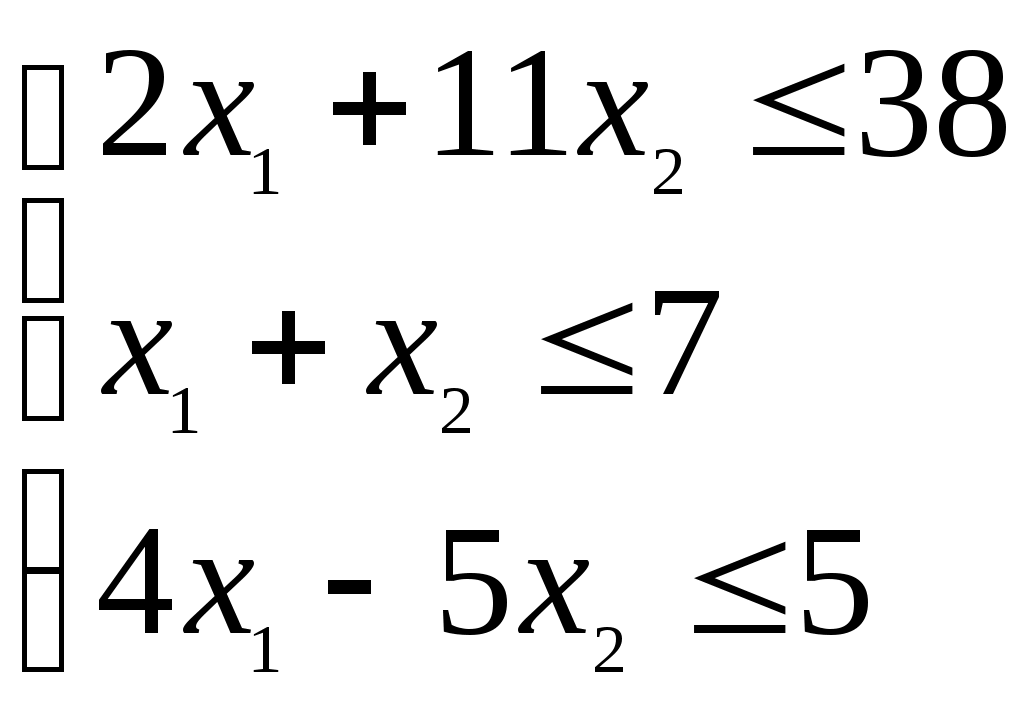
Z = 2x₁ +x₂ → max

Областью допустимых решений соответствующей задачи линейного программирования является многоугольник OABCD (см.рис.1), а оптимальное решение достигается в точке .

Отбросив обратные доли координат точки , получим точку X_ц(4;2), которая области допустимых решений задачи не принадлежит (нарушается третье ограничение). На самом деле оптимальное решение задачи целочисленного программирования достигается в точке (3;2), которая в отличие от задачи линейного программирования не принадлежат границе области допустимых решений.

Определение. Точки, координатами которых является целые числа, называется целочисленными.
Рис.1 (см. в конце темы)
Таким образом, для решения задач целочисленного программирования необходимы специальные методы. Они делятся на три группы:

1. 
   Методы отсечения или отсекающих плоскостей.
   
2. 
   Комбинаторные методы.
   
3. 
   Методы случайного поиска или эвристические методы
   

Познакомимся с идеями первых двух групп методов.

---