Файл: Решение Это положительный ряд, т е. ряд, у которого все члены неотрицательны. Запишем общий член данного ряда.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 28
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1.1.20. Исследовать ряд на сходимость, применяя 1-й признак сравнения. Указать общий член ряда, с которым сравнивается данный ряд.
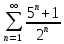
Решение:
Это положительный ряд, т.е. ряд, у которого все члены неотрицательны. Запишем общий член данного ряда:
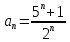 .
. Будем сравнивать ряд
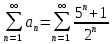 с рядом
с рядом 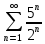 , применяя непредельный признак сравнения. Запишем общий член ряда
, применяя непредельный признак сравнения. Запишем общий член ряда 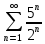 :
: 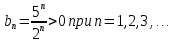
Применим непредельный признак сравнения.
Непредельный признак сравнения для рядов
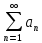 и
и 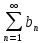 , причём
, причём 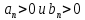 при
при 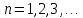 :
: 1) Если
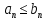 и сходится ряд
и сходится ряд 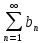 , тогда ряд
, тогда ряд 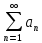 сходится.
сходится.2) Если
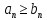 и расходится ряд
и расходится ряд 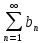 , тогда ряд
, тогда ряд 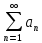 расходится
расходитсяРяд
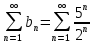 расходится, т.к.
расходится, т.к. 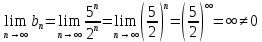 - не выполняется необходимый признак сходимости
- не выполняется необходимый признак сходимостиВ данном случае:
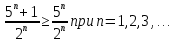 =>
=> 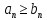
Ряд
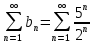 расходится. => Ряд
расходится. => Ряд 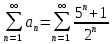 расходится по непредельному признаку сравнения.
расходится по непредельному признаку сравнения.Данный ряд
 расходится, общий член ряда, с которым сравнивается данный ряд:
расходится, общий член ряда, с которым сравнивается данный ряд: 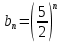 .
.Ответ: расходится,
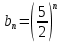 .
.1.1.29. Исследовать ряд на сходимость, применяя 2-й признак сравнения. Указать общий член ряда, с которым сравнивается данный ряд.
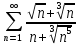
Решение:
Это положительный ряд, т.е. ряд, у которого все члены неотрицательны. Запишем общий член данного ряда:
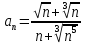 .
. Эквивалентность
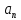 при
при 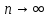 :
: 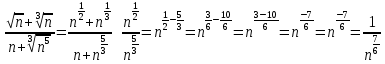
Будем сравнивать ряд
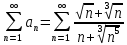 с рядом
с рядом 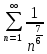 , применяя предельный признак сравнения. Запишем общий член ряда
, применяя предельный признак сравнения. Запишем общий член ряда 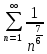 :
: 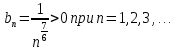
Предельный признак сравнения: если
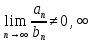 , причём
, причём  при
при  , то ряды
, то ряды  и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.В данном случае
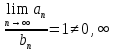 , так как
, так как 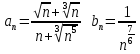 . => Ряд
. => Ряд 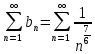 сходится, т.к. это обобщённый гармонический ряд вида
сходится, т.к. это обобщённый гармонический ряд вида 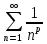 при
при 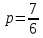 (при
(при 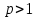 сходится, при
сходится, при 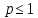 расходится). => Ряд
расходится). => Ряд 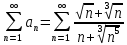 сходится по предельному признаку сравнения.
сходится по предельному признаку сравнения.
Данный ряд
 сходится, общий член ряда, с которым сравнивается данный ряд:
сходится, общий член ряда, с которым сравнивается данный ряд: 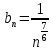 .
.Ответ: сходится,
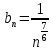 .
.1.1.32. Исследовать ряд на сходимость, применяя 2-й признак сравнения. Указать общий член ряда, с которым сравнивается данный ряд.
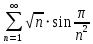
Решение:
Это положительный ряд, т.е. ряд, у которого все члены неотрицательны. Запишем общий член данного ряда:
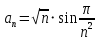 .
. Эквивалентность
 при
при  :
: 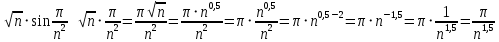
Будем сравнивать ряд
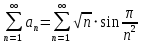 с рядом
с рядом 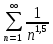 , применяя предельный признак сравнения. Запишем общий член ряда
, применяя предельный признак сравнения. Запишем общий член ряда 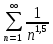 :
: 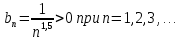
Предельный признак сравнения: если
 , причём
, причём  при
при  , то ряды
, то ряды  и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.В данном случае
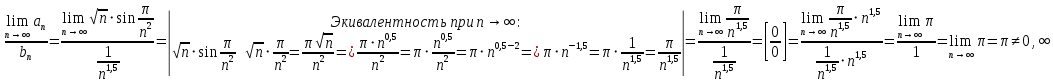 => Ряд
=> Ряд 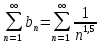 сходится, т.к. это обобщённый гармонический ряд вида
сходится, т.к. это обобщённый гармонический ряд вида  при
при 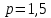 (при
(при  сходится, при
сходится, при  расходится). => Ряд
расходится). => Ряд 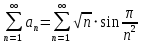 сходится по предельному признаку сравнения.
сходится по предельному признаку сравнения.Данный ряд
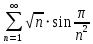
сходится, общий член ряда, с которым сравнивается данный ряд:
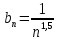 .
.Ответ: сходится,
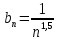 .
.1.1.38. Исследовать ряд на сходимость, применяя признак Даламбера. Указать
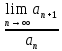 .
.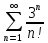
Решение:
Это положительный ряд, т.е. ряд, у которого все члены неотрицательны. Запишем общий член данного ряда:
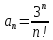 , тогда
, тогда 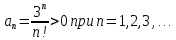
Используем признак Даламбера для ряда, у которого все члены положительные:
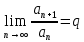 , где
, где  - общий член положительного ряда,
- общий член положительного ряда, 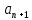 - следующий общий член положительного ряда
- следующий общий член положительного ряда Тогда следующий общий член данного ряда:
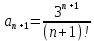
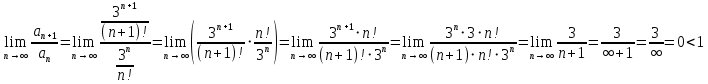
В данном случае
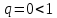 , тогда согласно признаку Даламбера данный ряд сходится.
, тогда согласно признаку Даламбера данный ряд сходится.Ответ: сходится,
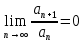 .
.1.1.48. Исследовать ряд на сходимость, применяя признак Даламбера. Указать
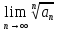 .
.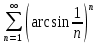
Это положительный ряд, т.е. ряд, у которого все члены неотрицательны. Запишем общий член данного ряда:
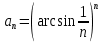 .
. Используем радикальный признак Коши для положительного ряда:
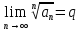 , где
, где  - это общий член данного ряда.
- это общий член данного ряда. 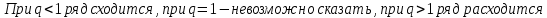 .
. 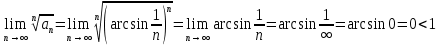
В данном случае
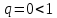 , тогда согласно радикальному признаку Коши данный ряд сходится.
, тогда согласно радикальному признаку Коши данный ряд сходится.
Ответ: сходится,
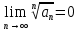 .
.1.1.53. Исследовать ряд на сходимость, применяя интегральный признак. Указать первообразную для функции
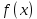 и
и 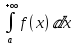 .
.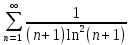
Решение:
Это положительный ряд, т.е. ряд, у которого все члены неотрицательны. Запишем общий член данного ряда:
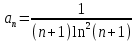 .
. Применим интегральный признак Коши:
Если
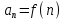 ,
,  - общий член данного ряда , где
- общий член данного ряда , где 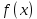 - это положительная функция и монотонно убывает и непрерывна при
- это положительная функция и монотонно убывает и непрерывна при 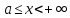 , тогда несобственный интеграл
, тогда несобственный интеграл 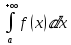 и ряд
и ряд 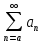 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.В данном случае
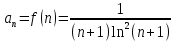 =>
=> 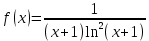
Рассмотрим соответствующую функцию
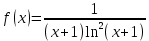 .
.Заметим, что функция
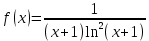 монотонно убывает на интервале
монотонно убывает на интервале 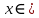 и функция непрерывна при
и функция непрерывна при 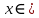 и
и 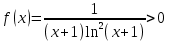 при всех
при всех 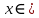 , т.е. положительна при
, т.е. положительна при 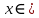 .
.=> Применим интегральный признак Коши.
Тогда вычислим несобственный интеграл
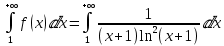 .
.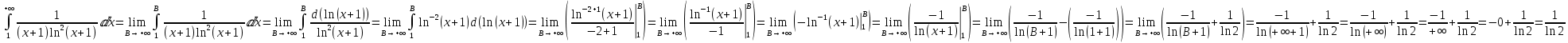
=> Несобственный интеграл
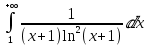 сходится
сходится => Ряд