Все значения Q_i оказались меньше Q_табл, следовательно, грубые промахи отсутствуют.

1. Расчет стандартного и относительного отклонений

Далее определим стандартное и относительное квадратичное отклонение для имеющихся данных. В фармакопее при анализе площадей пиков хроматограммы требуется достижения S_r = 0,02.



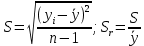
Таблица 7: Расчет среднеквадратичных отклонений.

Концентрация, нг/мл	Площадь пика, у.е.		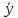S	Sr
Градуировочные растворы				Sr треб=	0,02
1	456317	545884,666	77662,0521	0,14226824
1	594492
1	586845
5	2633507	2865037,666	226498,01943	0,07905586
5	3086143
5	2875463
10	5713463	6047268,666	442960,65691	0,073249707
10	6549797
10	5878546
50	30238656	33346715,333	2710832,7075	0,0812923456
50	35222598
50	34578892
100	61184178	65054906,666	3376254,3653	0,051898535
100	67392997
100	66587545
500	294306804	298728279,0	6738369,0286	0,0225568502
500	305293871
500	296584162
1000	579393299	589299989,333	10617210,0223	0,018016647
1000	600507794
1000	587998875
5000	2481808295	2499694813,333	25888011,2321	0,01035646876
5000	2529380513
5000	2487895632
10000	4519803296	4466960644,0	49266353,4607	0,0110290547
10000	4422293382
10000	4458785254

---

1. Оценка значимости параметров уравнения регрессии

Оценка значимости уравнения регрессии в целом осуществляется с помощью критерия Фишера, так называемого F-критерия. При этом выдвигается нулевая гипотеза H₀, что коэффициент регрессии равен нулю, то есть b=0, а значит фактор х не оказывает влияния на результат у и линия регрессии параллельна оси абсцисс. Если гипотеза H₀ подтверждается, то факторная и остаточная дисперсии одинаковы и уравнение регрессии незначимо.

Если F_факт F_табл, тогда гипотеза H₀ отклоняется и делается вывод, что связь между y и x существенна и уравнение регрессии статистически значимо. Если же F_факт F_табл, тогда гипотеза H₀ принимается и делается вывод, что уравнение регрессии статистически незначимо, так как существует риск (при заданном уровне надежности) сделать неправильный вывод о наличии связи между x и y. Рассчитаем критерий Фишера:



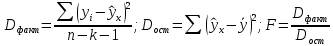
Таблица 8: Расчет F-критерия.

y	x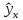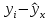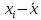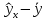
456317	1	196454611,68	-194372842,68	-1850,777778	-2136278028,21
2633507	5	201071650,11	-190378467,11	-1846,777778	-2131660989,78
5713463	10	206842948,14	-184754607,14	-1841,777778	-2125889691,75
34578892	50	253013332,37	-138440695,37	-1801,777778	-2079719307,52
67392997	100	310726312,66	-86362406,66	-1751,777778	-2022006327,23
305293871	500	772430154,98	127115398,02	-1351,777778	-1560302484,91
579393299	1000	1349559957,88	398030404,12	-851,7777778	-983172682,01
2481808295	5000	5966598381,09	626933636,91	3148,222222	3633865741,20
4519803296	10000	11737896410,10	-357770420,10	8148,222222	9405163770,21

---

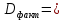1,27104E+20 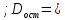1,18631E+17 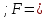1071,425926;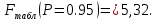

F_факт F_табл, следовательно, связь между y и x существенна и уравнение регрессии статистически значимо.

Также следует оценить значимость отдельных параметров членов регрессии. Для того, чтобы провести такое оценивание, для всех параметров рассчитываются стандартные ошибки: μ_k, μ_b.



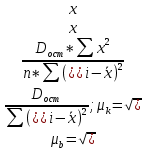
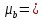35263,257; 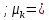132080461
Чтобы оценить существенность параметров, необходимо рассчитать для них критерии Стьюдента t_k, t_b. Для параметров a и b критерий Стьюдента определяет соотношение между самим параметром и его ошибкой.



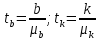
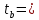5538,3526 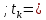114,42873
Табличное значение критерия Стьюдента при 0,05 и df=7 (прил. 3) равно 2,36. То есть, сравнив полученные нами фактические значения критериев Стьюдента для нашего примера с табличным значением, можно уверенно сделать вывод о существенности свободного члена уравнения регрессии k и коэффициента регрессии b, а также и о существенности всего уравнения в целом.

---

Смотрите также файлы

• Методические указания по проведению учебной практики для студентов агрономического факультета.doc

• Бухгалтерский баланс на 31 декабря 2021 г.docx

• Конспект лекции.pdf

• Элоуавт со вторичной переработкой бензина и др.pdf

• Практикум по совершенствованию двигательных умений и навыков Теоретические основы физического воспитания детей дошкольного возраста.docx