Добавлен: 09.11.2023
Просмотров: 18
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Автономная некоммерческая образовательная организация высшего образования «Сибирский институт бизнеса и информационных технологий»
РЕФЕРАТ
Дисциплина: Высшая математика
Тема: Высшая математика
Выполнил: студент группы ЭНБУААоз-1122(2)
Ф.И.О. Валиева Валентина Сергеевна
Город: Муравленко
Омск 2023
Кроссворд
Раздел 1. Линейная алгебра.
-
Виды матриц.
Разгадав чайнворд Вы узнаете фамилию математика, который в 1850 году ввел современное название “матрица”.
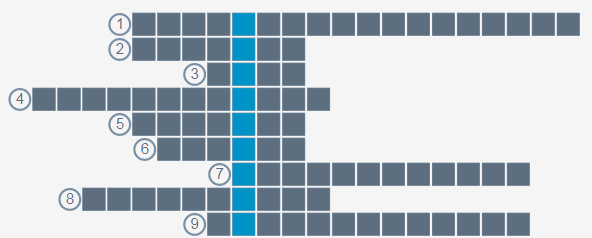
Вопросы по горизонтали:
-
Матрица, полученная из исходной матрицы заменой строк на столбцы -
Прямоугольная таблица, составленная из m х n элементов некоторого множества. -
Сумма диагональных элементов матрицы -
Квадратная матрица, все элементы которой, стоящие выше и ниже главной диагонали, равны нулю -
Матрица, все элементы которой нули -
Две цифры, которыми нумеруются элементы матрицы -
Квадратная матрица, совпадающая с транспортированной -
Матрица, у которой число строк равно числу ее столбцов -
Матрица, у которой число строк не равно числу столбцов
Современное название “матрица” было введено Джеймсом Сильвестром (1814–1897), в 1850 году.
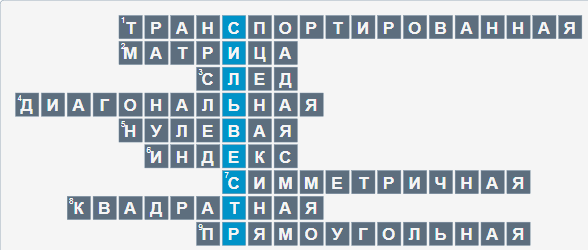
Ответы на кроссворд.
-
Транспортированная -
Матрица -
След -
Диагональная -
Нулевая -
Индекс -
Симметричная -
Квадратная -
Прямоугольная
Структурно-логическая схемаРаздел 2. Аналитическая геометрия
5. Кривые второго порядка.
| | Эллипс | Гипербола | Парабола |
| Определение | Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек (фокусов) есть величина постоянная | Гиперболой называется множество точек плоскости, разность расстояний которых до двух данных точек (фокусов) есть величина постоянная. | Параболой называется множество точек плоскости, равноудаленных от данной точки (фокуса) и данной прямой (директрисы) |
| Каноническое уравнение кривой с центром в начале координат | 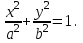 | 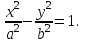 | у2 =2рх, p>0 x2 =2рy, p>0 |
| Каноническое уравнение кривой с центром в точке С (х0; у0) |  |  |  |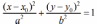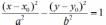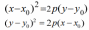
| Расположение кривых в зависимости от коэффициентов в уравнениях. | 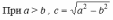  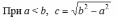 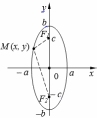 | 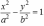 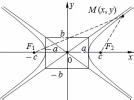 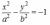 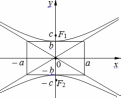 | у2 =2рх, p>0   |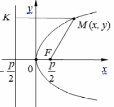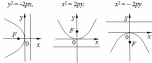
| Элементы кривой | 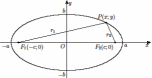 2а – большая ось эллипса 2b – меньшая ось эллипса    |  |   |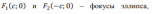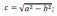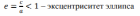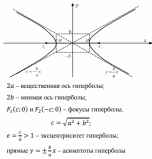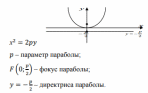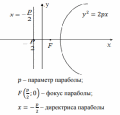
Тестовое задание на установление соответствия
Раздел 3. Введение в математический анализ
5. Непрерывность и точки разрыва
| № | Вопрос | Вариант ответа | ||||||||||
| 1 | По определению, функция f(x)называется непрерывной в точкеx0, если | A В Г |    | |||||||||
| 2 | По определению  , функция  называется непрерывной в точке  , если | A В Г Д |     | |||||||||
| 3 | Какие из перечисленных функций непрерывны в точке  : | 1 2 3 4 |     | |||||||||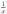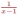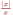
| 4 | Какие из перечисленных функций непрерывны в точке  : | 1 2 3 4 |   | |||||||||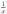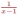
| 5 | Если функция непрерывна в точке и  ,то | А Б В |    | |||||||||
| 6 | Указать числовой промежуток, на котором функция  непрерывна: | А Б В Г |     | |||||||||
| 7 | Указать числовой промежуток, на котором функция  непрерывна: | А Б В Г |    | |||||||||
| 8 | Отметьте верные утверждения | 1 2 3 4 | если функция  непрерывна в точке , то функции  и непрерывны в этой точкеесли функции и непрерывны в точке , то функции непрерывна в этой точкеесли функция  непрерывна в точке , то функции и непрерывны в этой точке если функции и  непрерывны в точке , то функция непрерывна в этой точке | |||||||||
| 9 | Точками разрыва функции  являются точки х: | 1 2 3 4 | - 3 0 1 3 | |||||||||
| 10 | Установите соответствие между графиком функции и характером точки х=а. |
| А 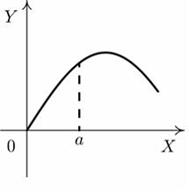 Б 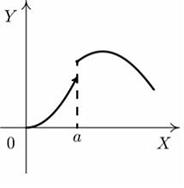 В 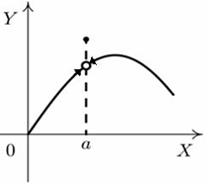 Г  | |||||||||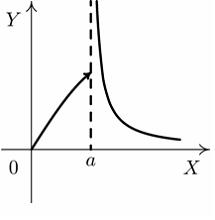
Ответы:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||
| А | А | 2,4 | 1,4 | В | В | В | 2,4 | 1,4 |
|