Урок может и должен стать увлекательным путешествием в мир математики, он должен дать возможность даже самому слабому ученику показать свой потенциал и творчество, почувствовать себя успешным.

Занимательные упражнения и задания дают возможность достичь маленькой победы. Дух соревнования стимулирует внимательное отношение к новому материалу. Игра превращает тяжелый труд заучивания в увлекательное занятие. Она таит богатейшие обучающие возможности. Игра помогает снять скованность, повышает внимание, оживляет, улучшает восприятие.

Игры бывают разные: индивидуальные, командные. Они могут быть посвящены закреплению пройденного материала, проверке математических знаний, выработке навыков и отработке умений быстрого и рационального счета. Одни игры длятся 5-7 минут, для других требуется целый урок.

Рассмотрев огромное количество игр, которые можно применять на уроках математики, некоторые игры вызвали интерес для их реализации. Игры, которые представлены ниже, понравились тем, что они универсальные. На примере этих игр можно составить подобные по разным темам курса математики. Также они не требуют особой подготовленности к уроку. От ученика требуется знание предмета, от преподавателя – подготовленные вопросы и план урока. Кроме того, в этих играх присутствует дух соревнования, а дети любят состязаться между собой. Игры, приведенные ниже, должны заинтересовать учеников.

1. 
   Игра «Горячий стульчик» (групповая) .
   

Цель: проверка знаний математических терминов по определенной теме, формулировок законов, теорем, аксиом и т.д.

Материал: не требует особой подготовки.

Ход игры: водящий садится на «горячий стульчик» у доски лицом к классу. Учащиеся по очереди задают ему вопросы по теме, оговоренной заранее.  Водящий должен ответить. Если допущена ошибка, водящий меняется на нового игрока, чей вопрос был последним.
Рассмотрим, например, тему «Умножение и деление натуральных чисел».

Примеры вопросов:

– Что такое деление?

– Как называют результат умножения?

– Существует ли сочетательное свойство умножения? Если да, то сформулируйте его.

– Существует ли сочетательное свойство деления? Если да, то сформулируйте его.

– В каких случаях можно опустить знак умножения?

---

Игру можно усложнить. Учащиеся дают объяснение математического термина, а водящий должен догадаться, что это за слово. Выигрывает тот, кто продержится на «горячем стульчике» дольше.

– С помощью этого действия находят неизвестный множитель (деление)

– Иногда деление одного натурального числа на другое нацело не всегда возможно, в этом случае получаем … (деление с остатком)

– Для того, чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения; это правило называется… (распределительное свойство умножения относительно сложения)

– Произведение, в котором все множители равны, можно записать короче. Эта запись называется … (степенью числа)

– Возведение во вторую степень (квадрат числа).

2. 
   Игра «Поле чудес» (индивидуальная) .
   

Цель: проверка знаний, умение применять теоремы и аксиомы при решении задач.

Материал: не требует особой подготовки.

Ход игры: учитель берет понравившееся ему высказывание или слова из песни, стихотворения, пословицу. По количеству букв в этом высказывании подбирается столько же задач так, чтобы одинаковым буквам соответствовали одинаковые ответы. Готовятся карточки желательно с дифференцированными заданиями, которые выдаются каждому ученику. На доске заранее должны быть записаны буквы, которые встречаются в высказывании, и под ними ответы, которые будут соответствовать этим буквам. Ниже должны быть записаны числа по порядку (по количеству букв в высказывании), соответствующие номерам карточек. Ученик, выполнивший задание, называет номер своей карточки и букву, под которой записан ответ. Например, карточка №5, буква А. Учитель под числом 5 ставит букву А. Если у ученика получилась другая буква, значит, он решил неверно, и у него есть время перерешать задачу, пока другие ребята еще решают свои задания. Те учащиеся, которые быстро справляются с заданием, получают следующую карточку. За правильно решенные 1-3 задания (на усмотрение учителя) ученик может получить оценку. Поэтому желательно карточек иметь больше, чем число учеников в классе.

Примеры вопросов (тема «Теорема Пифагора»):

1. В прямоугольной трапеции основания равны 5 и 17 см, а большая боковая сторона 13 см. Найдите площадь трапеции. (55).

---

2. В прямоугольной трапеции основания равны 12 и 6 см, а большая боковая сторона 10 см. Найдите площадь трапеции. (72)

3. В треугольнике ABC A=90, C=30, AB=6 см. Найдите сторону AC треугольника. ( )

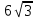4. Диагонали ромба равны 14 и 48 см. Найдите сторону ромба. (25).

5. Найдите катет прямоугольного треугольника, если его гипотенуза равна 10 см, а другой катет равен 8 см. (6).

В настоящее время в жизни людей компьютерные технологии имеют огромное значение. Они упрощают жизнь человека. Поэтому современный учитель должен уметь пользоваться этими технологиями и применять их на уроках. Далее приведен пример игры, которую можно провести на уроке математики, используя компьютер.

3. 
   Игра «Своя игра» (командная») .
   

Цели игры:

– учебная – повышение скорости вычисления; совершенствование, обобщение и закрепление знаний учащихся по предметам естественно-математического цикла;

– развивающая – развитие мышления, памяти, внимательности, интереса к изучению математики;

– воспитательная – развитие познавательного интереса, воспитание культуры общения и культуры математической речи. Воспитание чувства ответственности и солидарности.

Задачи игры

– Повторение и обобщение знаний.

– Формирование системно-информационного подхода к анализу окружающего мира.

– Формирование учебных и общекультурных навыков работы с информацией.

– Формирование умений и навыков, которые носят в современных условиях общенаучный, интеллектуальный характер.

Для проведения игры необходимо следующее оборудование:

компьютер и проектор, компьютерная презентация «Своя игра»,

вопросы викторины с ответами для учителя.

Ход игры: перед началом игры все учащиеся, желающие принять в ней участие, делятся на три сборные команды. Разделение осуществляется следующим образом. Капитаны (выбираются заранее) по очереди набирают себе команду из присутствующих. Сформированные таким образом команды рассаживаются за столы. В течение 2-х минут команды придумывают себе название и записывают его маркером на табличках, которые заранее приготовлены на столах. Учитель записывает названия команд в таблицу фиксирования результатов игры, заранее заготовленную на классной доске.

---

Игра состоит из трех раундов: 2 раунда по 25 вопросов, которые объединены в пять категорий и третий раунд – большая игра. В каждой категории вопросы различаются по цене (стоимости). На игровом поле записаны категории и очки. Участник выбирает вопрос по категории и по цене. Отвечает на вопрос тот, кто первым поднимет руку. При правильном ответе количество баллов игрока увеличивается, при неправильном – баллы снимаются. Отвечать надо быстро, ответы не обсуждаются.

Побеждает та команда, которая набрала больше баллов.

Далее приведу пример игры, разработанный мной для учеников 5 класса. Эту игру можно проводить в конце года во время итогового повторения.

Организация урока

1-й раунд

Категории вопросов, которые будут разыгрываться:

1. 
   Натуральные числа;
   
2. 
   Плоскость. Прямая. Луч;
   
3. 
   Сложение и вычитание натуральных чисел;
   
4. 
   Уравнение. Углы;
   
5. 
   Многоугольники.
   

В каждой категории по 5 вопросов различной сложности. За каждый правильный ответ команды могут получить от 10 до 50 баллов.

Вопросы для каждой категории

Натуральные числа

Какие числа называют натуральными?

Ответ: числа, используемые при счёте предметов, называются натуральными.

Есть ли среди натуральных чисел наименьшее число? Наибольшее число?

Ответ: среди натуральных чисел есть наименьшее число – это число 1, но нет наибольшего.

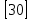На какие три разряда разбивается справа налево каждый класс?

Ответ: единицы, десятки, сотни.

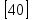Какая цифра не может стоять первой в записи натурального числа?

Ответ: 0.

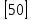Назовите все разряды числа 56324.

Ответ: 5 десятков тысяч 6 единиц тысяч 3 сотни 2 десятка 4 единиц.

Плоскость. Прямая. Луч

Почему нельзя изобразить плоскость?

Ответ: плоскость нельзя изобразить, потому что она бесконечна.

---

Имеет ли луч начало и конец?

Ответ: луч имеет только начало.

Сколько прямых проходит через две точки?

Ответ: через две точки проходить только одна прямая.

Что называют координатным лучом?

Ответ: координатный луч – на котором задано начало отсчета, единичный отрезок и показано направление увеличения чисел.

Назовите приборы, в которых используется координатный луч

Ответ: линейка, градусник, термометр и т.п.

Сложение и вычитание натуральных чисел

Какое из двух натуральных чисел, имеющих разное количество цифр, является меньшим?

Ответ: меньшим является то число, где меньше цифр.

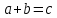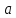В равенстве числа и 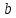называются…

Ответ: слагаемыми.

Как выглядит переместительное свойство сложения?

Ответ: от перестановки слагаемых сумма не меняется, т.е.

.

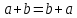Работает ли переместительное свойство для вычитания?

Ответ: не работает.

Как из суммы двух слагаемых можно вычесть число?

Ответ: чтобы из суммы двух слагаемых вычесть число, можно вычесть это число из одного из слагаемых (если это слагаемое больше или равно вычитаемому) и потом к результату прибавить другое слагаемое

Уравнение. Углы

Что называют корнем уравнения?

Ответ: корнем уравнения называют число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.

---

Смотрите также файлы

• 1. Назначение, конструкция и техническая характеристика коленчатых валов и их подшипников дизеля.rtf

• С. Боровлянское 2021 Чем заменить букетики полевых цветов Эколята дозиметр Участники проекта.pptx

• .rtf

• 6. 1 Анализ условий труда при прокладке кабеля.doc

• Физика пнінен 3тосана арналан жиынты баалауды тапсырмалары.docx