Файл: Тема Парная линейная регрессия.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 26

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Тема 1. Парная линейная регрессия

Вариант 10

Получены данные по 13 компаниям холдинга: х (тыс. $) – расходы на маркетинговые исследования, а у (млн. $) – прибыль компании. Признаки имеют нормальный закон распределения.

х
4,1
7,1
8,5
10,8
11,5
13,7
12,3
14,8
13,4
15,4
16,3
14,9
16,7

у
1,5
2,4
3,8
4,3
6,3
7,9
6
8,4
6,6
9,4
10,5
10
11

Задание:

  1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между расходами на маркетинговые исследования и прибылью компании.

  2. Рассчитайте оценки параметров уравнения парной линейной регрессии.

  3. Оцените тесноту связи между признаками с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции ( ).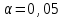

  4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.

  5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .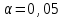

  6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.

  7. Составьте таблицу дисперсионного анализа.

  8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ( ).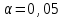

  9. Рассчитайте прибыль компании, если расходы на маркетинговые исследования составят 10 тыс. $. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.

  10. Рассчитайте средний коэффициент эластичности (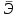 ). Сделайте экономический вывод.

  11. Определить среднюю ошибку аппроксимации.

  12. На поле корреляции постройте линию регрессии.

Тема 2. Множественная линейная регрессия

Вариант 10

По 25 странам изучается зависимость индекса человеческого развития у от переменных:

х1 – валовое накопление, % к ВВП;

х2 – расходы домашних хозяйств, % к ВВП.

Признак
Среднее значение
Среднее квадратическое отклонение
Парный коэффициент корреляции

у
0,85
0,1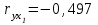


х1
21,74
5,61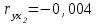


х2
58,74
6,07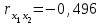


Задание:

1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.

2. Рассчитайте частные коэффициенты эластичности.

3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.

4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.

Приложение 1
Статистико-математические таблицы

Таблица значений F-критерия Фишера при уровне значимости

k2=n-m
k1=m-1

1
2
3
4
5
6
8
12
24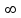


1
161,45
199,5
215,72
224,57
230,17
233,97
238,89
243,91
249,04
254,32

2
18,51
19,00
19,16
19,25
19,30
19,33
19,37
19,41
19,45
19,50

3
10,13
9,55
9,28
9,12
9,01
8,94
8,84
8,74
8,64
8,53

4
7,71
6,94
6,59
6,39
6,26
6,16
6,04
5,91
5,77
5,63

5
6,61
5,79
5,41
5,19
5,05
4,95
4,82
4,68
4,53
4,36

6
5,99
5,14
4,76
4,53
4,39
4,28
4,15
4,00
3,84
3,67

7
5,59
4,74
4,35
4,12
3,97
3,87
3,73
3,57
3,41
3,23

8
5,32
4,46
4,07
3,84
3,69
3,58
3,44
3,28
3,12
2,93

9
5,12
4,26
3,86
3,63
3,48
3,37
3,23
3,07
2,90
2,71

10
4,96
4,10
3,71
3,48
3,33
3,22
307
2,91
2,74
2,54

11
4,84
3,98
3,59
3,36
3,20
3,09
2,95
2,79
2,61
2,40

12
4,75
3,88
3,49
3,26
3,11
3,00
2,85
2,69
2,50
2,30

13
4,67
3,80
3,41
3,18
3,02
2,92
2,77
2,60
2,42
2,21

14
4,60
3,74
3,34
3,11
2,96
2,85
2,70
2,53
2,35
2,13

15
4,54
3,68
3,29
3,06
2,90
2,79
2,64
2,48
2,29
2,07

16
4,49
3,63
3,24
3,01
2,85
2,74
2,59
2,42
2,24
2,01

17
4,45
3,59
3,20
2,96
2,81
2,70
2,55
2,38
2,19
1,96

18
4,41
3,55
3,16
2,93
2,77
2,66
2,51
2,34
2,15
1,92

19
4,38
3,52
3,13
2,90
2,74
2,63
2,48
2,31
2,11
1,88

20
4,35
3,49
3,10
2,87
2,71
2,60
2,45
2,28
2,08
1,84

21
4,32
3,47
3,07
2,84
2,68
2,57
2,42
2,25
2,05
1,81

22
4,30
3,44
3,05
2,82
2,66
2,55
2,40
2,23
2,03
1,78

23
4,28
3,42
3,03
2,80
2,64
2,53
2,38
2,20
2,00
1,76

24
4,26
3,40
3,01
2,78
2,62
2,51
2,36
2,18
1,98
1,73

25
4,24
3,38
2,99
2,76
2,60
2,49
2,34
2,16
1,96
1,71

26
4,22
3,37
2,98
2,74
2,59
2,47
2,32
2,15
1,95
1,69

27
4,21
3,35
2,96
2,73
2,57
2,46
2,30
2,13
1,93
1,67

28
4,20
3,34
2,95
2,71
2,56
2,44
2,29
2,12
1,91
1,65

29
4,18
3,33
2,93
2,70
2,54
2,43
2,28
2,10
1,90
1,64

30
4,17
3,32
2,92
2,69
2,53
2,42
2,27
2,09
1,89
1,62

35
4,12
3,26
2,87
2,64
2,48
2,37
2,22
2,04
1,83
1,57

40
4,08
3,23
2,84
2,61
2,45
2,34
2,18
2,00
1,79
1,51

45
4,06
3,21
2,81
2,58
2,42
2,31
2,15
1,97
1,76
1,48

50
4,03
3,18
2,79
2,56
2,40
2,29
2,13
1,95
1,74
1,44

60
4,00
3,15
2,76
2,52
2,37
2,25
2,10
1,92
1,70
1,39



70
3,89
3,13
2,74
2,50
2,35
2,23
2,07
1,89
1,67
1,35



80
3,96
3,11
2,72
2,49
2,33
2,21
2,06
1,88
1,65
1,31



90
3,95
310
2,71
2,47
2,32
2,20
2,04
1,86
1,64
1,28



100
3,94
3,09
2,70
2,46
2,30
2,19
2,03
1,85
1,63
1,26



125
3,92
3,07
2,68
2,44
2,29
2,17
2,01
1,83
1,60
1,21



150
3,90
3,06
2,66
2,43
2,27
2,16
2,00
1,82
1,59
1,18



200
3,89
3,04
2,65
2,42
2,26
2,14
1,98
1,80
1,57
1,14



300
3,87
3,03
2,64
2,41
2,25
2,13
1,97
1,79
1,55
1,10



400
3,86
3,02
2,63
2,40
2,24
2,12
1,96
1,78
1,54
1,07



500
3,86
3,01
2,62
2,39
2,23
2,11
1,96
1,77
1,54
1,06



1000
3,85
3,00
2,61
2,38
2,22
2,10
1,95
1,76
1,53
1,03





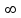3,84
2,99
2,60
2,37
2,21
2,09
1,94
1,75
1,52
1,00




Приложение 2

Критические значения t–критерия Стьюдента при уровне значимости 0,10; 0,05; 0,01 (двухсторонний)


Число степеней свободы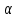


Число степеней свободы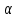


0,10
0,05
0,01
0,10
0,05
0,01

1
6,3138
12,706
63,657
18
1,7341
2,1009
2,8784

2
2,9200
4,3027
9,9248
19
1,7291
2,0930
2,8609

3
2,3534
3,1825
5,8409
20
1,7247
2,0860
2,8453

4
2,1318
2,7764
4,6041
21
1,7207
2,0796
2,8314

5
2,0150
2,5706
4,0321
22
1,7171
2,0739
2,8188

6
1,9432
2,4469
3,7074
23
1,7139
2,0687
2,8073

7
1,8946
2,3646
3,495
24
1,7109
2,0639
2,7969

8
1,8595
2,3060
3,3554
25
1,7081
2,0595
2,7874

9
1,8331
2,2622
3,2498
26
1,7056
2,0555
2,7787

10
1,8125
2,2281
3,1693
27
1,7033
2,0518
2,7707

11
1,7959
2,2010
3,1058
28
1,7011
2,0484
2,7633

12
1,7823
2,1788
3,0545
29
1,6991
2,0452
2,7564

13
1,7709
2,1604
3,0123
30
1,6973
2,0423
2,7500

14
1,7613
2,1448
2,9768
40
1,6839
2,0211
2,7045

15
1,7530
2,1315
2,9467
60
1,6707
2,0003
2,6603

16
1,7459
2,1199
2,9208
120
1,6577
1,9799
2,6174

17
1,7396
2,1098
2,8982


1,6449
1,9600
2,5758



Приложение 3

Решение типовых заданий

Тема 1. Парная линейная регрессия

1. Рассчитайте оценки параметров парной линейной регрессии, где у – расходы на покупку продовольственных товаров, % к общему объему расходов, а х – среднемесячная заработная плата 1 работника, тыс. руб.

Параметры а и b линейной регрессии 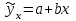рассчитываются в результате решения системы нормальных уравнений относительно а и b: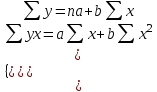



По исходным данным рассчитаем .

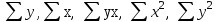Система нормальных уравнений составит:



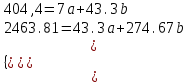
Решаем ее методом определителей: определитель системы ∆ равен:

,

,

,

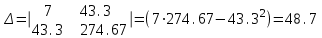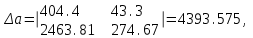
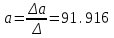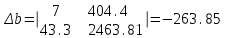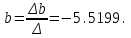
Получаем уравнение регрессии: .

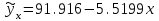Этот же результат можно получить, используя следующие формулы для нахождения параметров:

, ,

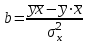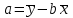где 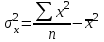- дисперсия по факторному признаку.

Таблица 1. – Расчетные данные

Номер региона
х
у
ху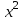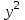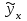






у-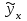

1
4,5
68,8
309,6
20,25
4733,44
67,1
1,7

2
5,9
58,3
343,97
34,81
3398,89
59,3
-1,0

3
5,7
62,6
356,82
32,49
3918,76
60,4
2,2

4
7,2
52,1
375,12
51,84
2714,41
52,2
-0,1

5
6,2
54,5
337,9
38,44
2970,25
57,7
-3,2

6
6
57,1
342,6
36
3260,41
58,8
-1,7

7
7,8
51
397,8
60,84
2601,00
48,9
2,1

Сумма
43,3
404,4
2463,81
274,67
23597,16
404,4
0

Среднее значение
6,186
57,77
351,97
39,24
3371,02
-
-

Смотрите также файлы