ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема 2. Множественная линейная регрессия
Имеются данные по 30 территориям России
Линейное уравнение множественной регрессии у от х1 и х2 имеет вид: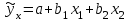
. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: 
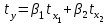. Расчет β – коэффициентов выполним по формулам
.
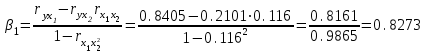
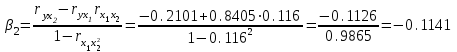Получим уравнение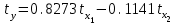
.
Для построения уравнения в естественной форме рассчитаем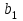
и 
, и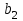спользуя формулы для перехода от βi к 
:
; 
;
; 
.
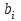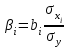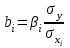
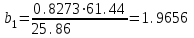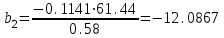Значение a определим из соотношения
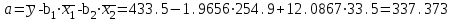
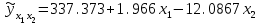
Рассчитаем средние коэффициенты эластичности для определения относительной силы влияния х1 и х2 на у:
; 
.
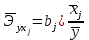
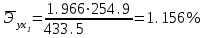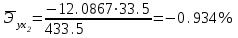С увеличением средней заработной платы х1 на 1% от ее среднего уровня средний душевой доход у возрастет на 1,16 % от своего среднего уровня; при повышении среднего возраста безработного х2 на 1 % среднедушевой доход у снижается на 0,93 % от своего среднего уровня. Очевидно, что сила влияния средней заработной платы х1 на средний душевой доход у оказалась большей, чем сила влияния среднего возраста безработного х2. К аналогичным выводам о силе связи приходим при сравнении модулей значений β1 и β2.
Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле:
;
.
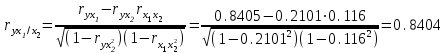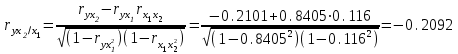При сравнении значений коэффициентов парной и частной корреляции приходим к выводу, что из-за слабой межфакторной связи (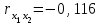
) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:
; ;
; 
; 
.
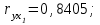
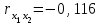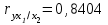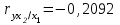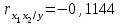
Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов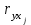
и βi:
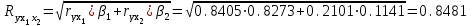
Зависимость у от х1 и х2 характеризуется как тесная, в которой 72 % вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28 % от общей вариации у.
Общий F – критерий проверяет гипотезу Н0 о статистической значимости уравнения регрессии и показателя тесноты связи (R2=0):
;
.
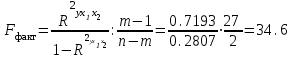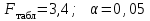Сравнивая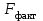
и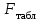 
, приходим к выводу о необходимости отклонить гипотезу Н0, т.к. 
<
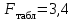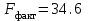. С вероятностью 1-α=0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи 
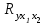, которые сформировались под неслучайным воздействием факторов х1 и х2.
Имеются данные по 30 территориям России
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у | 433,5 | 61,44 |  |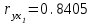
| х1 | 254,9 | 25,86 |  |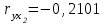
| х2 | 33,5 | 0,58 |  |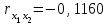
-
Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
Линейное уравнение множественной регрессии у от х1 и х2 имеет вид:
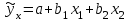. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: 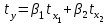. Расчет β – коэффициентов выполним по формулам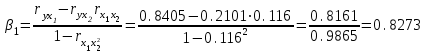 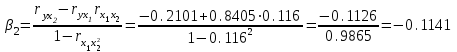.Получим уравнение
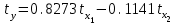.Для построения уравнения в естественной форме рассчитаем
и , используя формулы для перехода от βi к : ;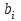
;
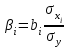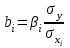
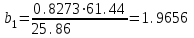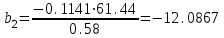; .Значение a определим из соотношения
-
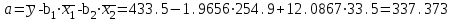
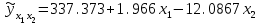
Рассчитайте частные коэффициенты эластичности.
Рассчитаем средние коэффициенты эластичности для определения относительной силы влияния х1 и х2 на у:
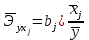
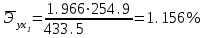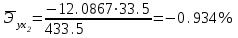; .С увеличением средней заработной платы х1 на 1% от ее среднего уровня средний душевой доход у возрастет на 1,16 % от своего среднего уровня; при повышении среднего возраста безработного х2 на 1 % среднедушевой доход у снижается на 0,93 % от своего среднего уровня. Очевидно, что сила влияния средней заработной платы х1 на средний душевой доход у оказалась большей, чем сила влияния среднего возраста безработного х2. К аналогичным выводам о силе связи приходим при сравнении модулей значений β1 и β2.
-
Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле:
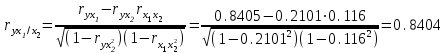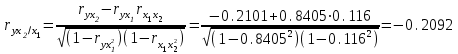; .При сравнении значений коэффициентов парной и частной корреляции приходим к выводу, что из-за слабой межфакторной связи (
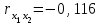) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают: ; ; ; ;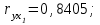
.
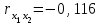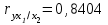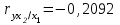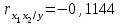
Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов
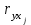и βi: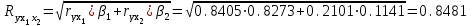 Зависимость у от х1 и х2 характеризуется как тесная, в которой 72 % вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28 % от общей вариации у.
-
Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Общий F – критерий проверяет гипотезу Н0 о статистической значимости уравнения регрессии и показателя тесноты связи (R2=0):
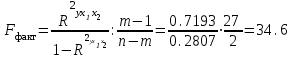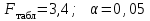; . Сравнивая
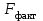и 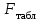, приходим к выводу о необходимости отклонить гипотезу Н0, т.к. 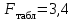< 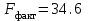. С вероятностью 1-α=0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи 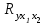, которые сформировались под неслучайным воздействием факторов х1 и х2.