ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 118
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Кинематическая вязкость газовой смеси вычисляется по формуле Манна
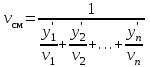 , (3.64)
, (3.64)где
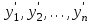 – содержание компонентов и газовой смеси, покидающей реактор, мольн. доли;
– содержание компонентов и газовой смеси, покидающей реактор, мольн. доли; 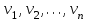 – кинематическая вязкость компонентов при средней температуре в реакторе, м/с2.
– кинематическая вязкость компонентов при средней температуре в реакторе, м/с2.Кинематическая вязкость углеводородов при температуре
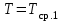
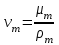 , (3.65)
, (3.65)где
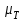 – динамическая вязкость, Паc;
– динамическая вязкость, Паc; 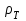 – плотность углеводородов, кг/м3.
– плотность углеводородов, кг/м3.Для расчёта динамической вязкости газов используем формулу
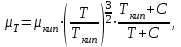 (3.66)
(3.66)где
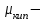 вязкость при температуре кипения;
вязкость при температуре кипения; 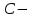 постоянная Сатерленда.
постоянная Сатерленда.Постоянную Сатерленда рассчитаем по формуле
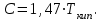 (3.67)
(3.67)Вязкость при температуре кипения рассчитаем по формуле Мейсснера:
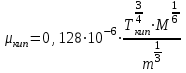 , (3.68)
, (3.68)где
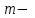 число атомов в молекуле газа.
число атомов в молекуле газа.Температуру кипения компонентов ВСГ определим по [10]. Для определения средней температуры кипения ароматических, нафтеновых и парафиновых углеводородов воспользуемся номограммой (рисунок 11), зная молекулярную массу и
 .
.Среднее число атомов в молекуле газа для ароматических, нафтеновых и парафиновых углеводородов определим, зная среднюю молекулярную массу углеводородов и их структурные формулы, т.к. под средней молекулярной массой подразумевается
молекулярная масса гипотетического углеводорода, имеющего усреднённые значения элементного состава, температуры кипения и плотности. Например, ароматические углеводороды
 в первом реакторе имеют среднюю молекулярную массу 109,72. Значит,
в первом реакторе имеют среднюю молекулярную массу 109,72. Значит,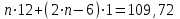
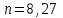
Следовательно, структурная формула усреднённого ароматического углеводорода
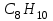 , т.е.
, т.е. 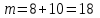 .
.Аналогично определяется и число атомов усреднённых нафтенового и парафинового углеводородов.
Далее необходимо учесть повышенное давление в реакторе. Для этого воспользуемся формулой Гарднера
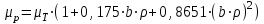 , (3.69)
, (3.69)где
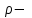 плотность газа, г/см3;
плотность газа, г/см3; 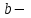 поправка, см3/г.
поправка, см3/г.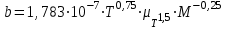 . (3.70)
. (3.70)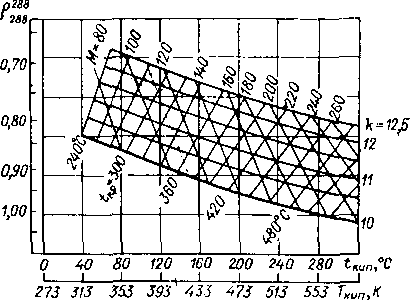
Рисунок 11 – Номограмма для определения характеристик топлива по двум заданным параметрам
Результаты расчётов динамической вязкости компонентов реакционной смеси представлены в таблице 3.21.
Таблица 3.21 - Расчёт динамической вязкости
| Компоненты | 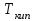 | С | m | 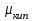 , Па·с , Па·с |  , Па·с , Па·с | b | 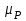 , Па·с , Па·с |
| Н2 | 20,23 | 29,74 | 2 | 1,09·10-6 | 1,60·10-5 | 1,41·10-12 | 1,60·10-5 |
| СН4 | 111,51 | 163,92 | 5 | 4,08·10-6 | 2,19·10-5 | 1,34·10-12 | 2,19·10-5 |
| С2Н6 | 184,37 | 271,02 | 8 | 5,64·10-6 | 2,12·10-5 | 1,09·10-12 | 2,12·10-5 |
| С3Н8 | 230,93 | 339,47 | 11 | 6,41·10-6 | 2,02·10-5 | 9,20·10-13 | 2,02·10-5 |
| С4Н10 | 272,50 | 400,58 | 14 | 7,01·10-6 | 1,92·10-5 | 8,01·10-13 | 1,92·10-5 |
| С5Н12 | 300,85 | 442,25 | 17 | 7,33·10-6 | 1,85·10-5 | 7,16·10-13 | 1,85·10-5 |
 | 373,00 | 548,31 | 18 | 9,07·10-6 | 1,89·10-5 | 6,65·10-13 | 1,89·10-5 |
 | 403,00 | 592,41 | 24 | 8,81·10-6 | 1,71·10-5 | 5,65·10-13 | 1,71·10-5 |
 | 402,00 | 590,94 | 26 | 8,59·10-6 | 1,67·10-5 | 5,43·10-13 | 1,67·10-5 |
Расчёт кинематической вязкости смеси представлен в таблице 3.22.
Кинематическая вязкость газовой смеси, согласно формуле Манна и данным таблицы 3.22, равна

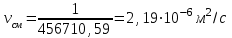 .
.Таблица 3.22 - Расчёт кинематической вязкости
| Компонент | Мольная доля  , , | 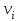 , , 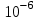 м2/с м2/с | 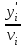 , с/м2 , с/м2 |
| Н2 | 0,7880 | 14,89 | 52935,54 |
| СН4 | 0,0369 | 2,55 | 14495,39 |
| С2Н6 | 0,0455 | 1,31 | 34703,43 |
| С3Н8 | 0,0283 | 0,85 | 33203,06 |
| С4Н10 | 0,0110 | 0,62 | 17852,01 |
| С5Н12 | 0,0110 | 0,48 | 23037,38 |
 | 0,0278 | 0,32 | 86848,09 |
 | 0,0094 | 0,27 | 34206,48 |
 | 0,0421 | 0,26 | 159429,21 |
| Сумма | 1,0000 | – | 456710,59 |
Подставив в формулу для расчета потери напора числовые значения величин, получим
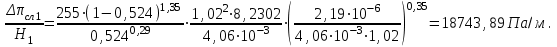
Толщина слоя катализатора в стакане
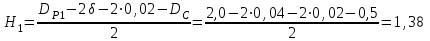 м.
м.Потеря напора в слое катализатора
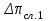 = 18743,89 ∙ 1,38 = 25866,57 Па.
= 18743,89 ∙ 1,38 = 25866,57 Па.Полученная числовая величина
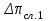 = 25866,57 Па не превышает [
= 25866,57 Па не превышает [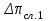 ] = 72 500 Па. При получении
] = 72 500 Па. При получении 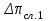 > [
> [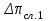 ] необходимо уменьшить толщину слоя катализатора, что достигается уменьшением диаметра Dpl аппарата.
] необходимо уменьшить толщину слоя катализатора, что достигается уменьшением диаметра Dpl аппарата.Полная высота реактора равна
Нп1 = Нсл.1 + 0,2 + DРl+ 0,225 + DРl + 0,425;
Нп1 =2,79 + 0,2 + 2,0 + 0,225 + 2,0 + 0,425=7,64 м.
Далее по аналогии производятся расчеты второго и третьего реакторов.