Добавлен: 09.11.2023
Просмотров: 26
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Содержание
Введение................................................................................................................3
1. Виды измерений............................................................................................5
2. Абсолютная погрешность.............................................................................6
Заключение.......................................................................................................14
Список литературы.........................................................................................15
Введение
Измерения физических величин и получение их числовых значений являются непосредственной задачей многих физических экспериментов. Выведенные в результате измерений физические законы приводятся в виде формул, которые показывают, как числовые значения одних величин могут быть найдены по числовым значениям других.
Получение надёжных числовых значений не является простой задачей из-за погрешностей, неизбежно возникающих при измерениях. Мы рассмотрим эти погрешности, а также методы, применяемые при обработке результатов измерений.
Владение этими методами нужно для того, чтобы научиться получать из совокупности измерений наиболее близкие к истине результаты, вовремя заметить несоответствия и ошибки, разумно организовать сами измерения и правильно оценить точность полученных значений.
Произвести измерения физических величин абсолютно точно невозможно, так как всякое измерение сопровождается той или иной ошибкой или погрешностью. Другими словами, измеренное значение величины всегда отличается от истинного ее значения. Задачей экспериментатора является не только нахождение самой величины, но и оценка допущенной при измерении погрешности.
Результат любого измерения отличается от истинного значения измеряемой величины на некоторое значение, зависящее от точности средств и метода измерения, квалификации оператора, условий, при которых производится измерение. Отклонение результата измерения от истинного значения измеряемой величины называется погрешностью измерения.
1.Виды измерений
Принято различать прямые и косвенные измерения. Прямые измерения производятся с помощью приборов, которые измеряют непосредственно саму исследуемую величину. Так, падение напряжения на сопротивлении можно найти по вольтметру
, длину стержня измерить линейкой, а время — секундомером. К косвенным относятся измерения таких физических величин, для нахождения которых необходимо использовать связь в виде формулы с другими, непосредственно измеряемыми величинами. Например, площадь прямоугольника находят по измерению длин его сторон, электрическое сопротивление — по измерению силы тока и напряжения. При косвенном измерении искомую величину находят с помощью прямых измерений других величин, связанных с искомой величиной известной зависимостью. Интересующая нас величина находится путём соответствующих расчётов. Качество измерений определяется их точностью. При прямых измерениях точность опытов устанавливается из анализа точности метода и прибора, а также из повторяемости результатов измерений.
Точность косвенных измерений зависит как от надёжности используемых для расчёта данных, так и от структуры формул, связывающей эти данные с искомой величиной.
Очень важно при измерениях рассчитывать погрешность, чтобы получить более точный результат. Важно также знать причины возникновения погрешностей. Причинами возникновения погрешностей являются: несовершенство методов измерений, технических средств, применяемых при измерениях, и органов чувств наблюдателя. В отдельную группу следует объединить причины, связанные с влиянием условий проведения измерений. Последние проявляются двояко. С одной стороны, все физические величины, играющие какую-либо роль при проведении измерений, в той или иной степени зависят друг от друга. Поэтому с изменением внешних условий изменяются истинные значения измеряемых величин. С другой стороны, условия проведения измерений влияют и на характеристики средств измерений и физиологические свойства органов чувств наблюдателя и через их посредство становятся источником погрешностей измерения.
2. Абсолютная погрешность
При любой степени совершенства и точности измерительной аппаратуры, рационально спланированной методике измерений, тщательности выполнения измерительных операций результат измерений отличается от истинного значения физической величины.
Иначе говоря, при всяком измерении неизбежны обусловленные разнообразными причинами отклонения результата измерения (x) от истинного значения измеряемой величины (X). Эти отклонения называют погрешностями измерений.
Это соотношение служит исходным для теоретического анализа погрешностей. На практике же из-за невозможности определить истинное значение вместо него берут действительное значение измеряемой величины, например, среднеарифметическое результатов наблюдений при измерениях с многократными наблюдениями.
Истинным называется значение ФВ (физической величины), идеальным образом характеризующее свойство данного объекта, как в количественном, так и качественном отношении. Оно не зависит от средств нашего познания и является той абсолютной истиной, к которой мы стремимся, пытаясь выразить её в виде числовых значений.
Действительным называется значение ФВ, найденное экспериментально и настолько близкое к истинному, что в поставленной измерительной задаче оно может быть использовано вместо него.
Погрешность измерений иногда удобно характеризовать ее относительным значением:
Следует также различать погрешность результата измерения и погрешность средства измерений (СИ). Эти два понятия во многом близки друг к другу и классифицируются по одинаковым признакам.
Погрешность средства измерений – разность между показанием СИ и истинным (действительным) значением измеряемой ФВ. Она характеризует точность средства измерений (характеристику качества СИ, отражающую близость его погрешности к нулю).
Величину, обратную относительной погрешности, называют точностью:
Чем выше точность, тем с меньшей погрешностью произведено измерение. Обычно понятие точности используют для сравнительной характеристики различных измерений или средств измерений.
Правильное количественное представление о качестве измерений получают путем указания погрешности или точности. Соответствующие формулировки будут:
-
с погрешностью до 1 мВ; -
с относительной погрешностью до 0,1%; -
с точностью 1000.
Точность 1000 соответствует относительной погрешности 0,1%, точность 25 – относительной погрешности 4%.
Чтобы правильно оценивать погрешность, следует ясно представлять ее происхождение, понимать, к какому виду относится данная составляющая погрешности измерений. Это диктует необходимость рассмотрения классификации погрешностей. Их можно классифицировать по многим признакам, но мы постараемся сделать это наиболее полным образом.
По характеру проявления погрешности делятся на случайные, систематические, прогрессирующие и промахи, или грубые погрешности.
Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера физической величины, проведенных с одинаковой тщательностью в одних и тех же условиях.
В появлении таких погрешностей, изображенных на рис. 2.1(а), не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения, однако их можно существенно уменьшить, увеличив число наблюдений.
Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же физической величины. Постоянная и переменная систематические погрешности показаны на рис. 2.1(б). Их отличительный признак заключается в том, что они могут быть предсказаны, обнаружены и благодаря этому почти полностью устранены введением соответствующей поправки.
Прогрессирующая (дрейфовая) погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени. Прогрессирующие погрешности могут быть скорректированы поправками только в данный момент времени, а далее вновь непредсказуемо изменяются. Их изменение во времени представляет собой нестационарный случайный процесс, поэтому в рамках хорошо разработанной теории стационарных случайных процессов они могут быть описаны лишь с известными оговорками.
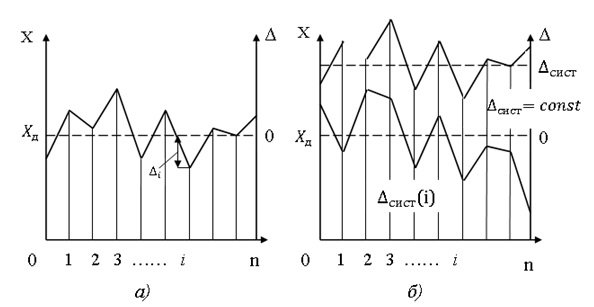
Рис. 2.1. Изменение: а – случайной, б – постоянной и переменной систематических погрешностей от измерения к измерению
Прогрессирующая погрешность – это понятие, специфичное для нестационарного случайного процесса изменения погрешности во времени, оно не может быть сведено к понятиям случайной и систематической погрешностей.
По способу выражения разделяют абсолютные, относительные и приведенные погрешности.
Алгебраическую разность измеряемого значения величины x и действительного ее значения a называют абсолютной погрешностью измерения
Отношение абсолютной погрешности к действительному значению измеряемой величины
Отношение абсолютной погрешности к максимальному возможному значению измеряемой величины (например, к верхнему пределу измерений прибора или к диапазону измерений) называется приведенной погрешностью
В зависимости от причин возникновения различают инструментальные погрешности измерения, погрешности метода измерений, погрешности из-за изменения условий измерения и субъективные погрешности измерения.
Инструментальная погрешность измерения обусловлена погрешностью применяемого СИ. Иногда эту погрешность называют аппаратурной.
Погрешность метода измерений – составляющая систематической погрешности измерений из-за несовершенства принятого метода измерений, эта погрешность обусловлена:
-
отличием принятой модели объекта измерения от модели, адекватно описывающей его свойство, которое определяется путем измерения; -
влиянием способов применения СИ. Это имеет место, например, при измерении напряжения вольтметром с конечным значением внутреннего сопротивления. В таком случае вольтметр шунтирует участок цепи, на котором измеряется напряжение, и оно оказывается меньше, чем было до присоединения вольтметра; -
влиянием алгоритмов (формул), по которым производятся вычисления результатов измерений. Вследствие упрощений, принятых в уравнениях для измерений, нередко возникают существенные погрешности, для компенсации действия которых следует вводить поправки. Иногда погрешность метода называют теоретической погрешностью; -
влиянием других факторов, не связанных со свойствами используемых СИ.