Добавлен: 09.11.2023
Просмотров: 27
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Отличительной особенностью погрешностей метода является то, что они не могут быть указаны в документации на используемое СИ, поскольку от него не зависят; их должен определять оператор в каждом конкретном случае. В связи с этим оператор должен четко различать фактически измеряемую им величину и величину, подлежащую измерению. Иногда погрешность метода может проявляться как случайная.
Погрешность (измерения) из-за изменения условий измерения – это составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля, вибрации и др.); неправильной установки средств измерений, нарушения правил их взаимного расположения и др.
Субъективная (личная) погрешность измерения обусловлена погрешностью отсчета оператором показаний по шкалам СИ, диаграммам регистрирующих приборов. Она вызвана состоянием оператора, его положением во время работы, несовершенством органов чувств, эргономическим свойствами СИ.
По зависимости абсолютной погрешности от значений измеряемой величины различают погрешности: аддитивные
, не зависящие от измеряемой величины; мультипликативные 
, которые прямо пропорциональны измеряемой величине, и нелинейные 
, имеющие нелинейную зависимость от измеряемой величины.Эти погрешности применяют в основном для описания метрологических характеристик средств измерений. Такое их разделение весьма существенно при решении вопроса о нормировании и математическом описании погрешностей СИ.
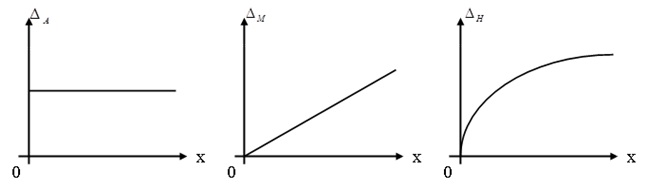
Рис. 2.2. Аддитивная (а), мультипликативная (б) и нелинейная (в) погрешности
По влиянию внешних условий различают основную и дополнительную погрешности средств измерений. Основная погрешность средства измерений – погрешность СИ, применяемого в нормальных условиях. Для каждого средства оговариваются условия эксплуатации, при которых нормируется его погрешность. Дополнительная погрешность средства измерений – составляющая погрешности СИ, возникающая дополнительно к основной погрешности, вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений.
В зависимости от влияния характера изменения измеряемых величин погрешности СИ делят на статические и динамические. Статической называется погрешность средства измерений, применяемого для измерения ФВ, принимаемой за неизменную. Динамической называется погрешность СИ, возникающая дополнительно при измерении изменяющейся (в процессе измерений) ФВ.
Динамическая погрешность СИ обусловлена несоответствием его реакции на скорость (частоту) изменения измеряемого сигнала.
Заключение
Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.
Абсолютная погрешность вычисляется по следующей формуле:
ΔQn =Qn −Q0,
где AQn – абсолютная погрешность;
Qn – значение некой величины, полученное в процессе измерения;
Q0 – значение той же самой величины, принятое за базу сравнения (настоящее значение).
Абсолютная погрешность меры – это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины.
Относительная погрешность – это число, отражающее степень точности измерения. Относительная погрешность выражается в процентах.
Приведенная погрешность – это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению.
Список литературы
1. Воронцов Л.Н. Федотов. Взаимозаменяемость, стандартизация и технические измерения. - 6-е изд., перераб. и доп.. -- М.: Машиностроение, 2018. - 352 с.
2. Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др. Лабораторные занятия по физике. Учебное пособие / под ред. Гольдина Л. Л.. - М.: Наука. Главная редакция физико-математической литературы, 2017. - 704 с.
3. Деденко Л. Г., Керженцев В. В. Математическая обработка и оформление результатов эксперимента. -- М.: МГУ, 2018. - 111 с.
4. Назаров Н.Г. Метрология. Основные понятия и математические модели. - М.: Высшая школа, 2019. - 348 с.
5. Рабинович С.Г. Погрешности измерений. - Ленинград, 2018. - 262 с.
6. Фридман А.Э. Основы метрологии. Современный курс. -- Санкт-Петербург: НПО «Профессионал», 2018. - 284 с.
7. Широков Ю. М., Юдин Н. П. Ядерная физика. - М.: Наука,2019. - 670 с.