Министерство образования и науки

Российской Федерации
Санкт-Петербургский государственный

архитектурно-строительный университет
Факультет инженерной экологии и городского хозяйства
Кафедра городского хозяйства, геодезии, землеустройства и кадастров
ГЕОДЕЗИЯ

Методические указания
Орехов Михаил Михайлович +7-921-373-48-92,

Соловьев Александр Николаевич (812) 670-92-46

Терещенко Татьяна Юрьевна +7-921-949-99-34

Волков Алексей Васильевич +7-911-211-63-27

Санкт-Петербург

2016
УДК 528.48:69
Рецензент канд. воен. наук, доцент В. Н. Зиновьев (СПбГАСУ)
Геодезия: метод. указания / сост.: М. М. Орехов, А. Н. Соловьев, Т. Ю. Терещенко, А. В. Волков; СПбГАСУ. – СПб., 2016. – с.


Содержание методических указаний соответствует программе дисциплин «Геодезия» и «Геодезия и картография» для обучения по направлениям «Строительство», «Архитектура», «Землеустройство и кадастры» и помогает студентам очной и заочной форм обучения самостоятельно выполнять расчетно-графическую работу по топографической карте.

Методические указания включают рассмотрение восьми задач входящих в расчетно-графическую работу по определению полных прямоугольных координат, геодезических координат, нанесению точек на топографическую карту по заданным координатам, построение линий заданного уклона, вычисление графически и аналитически площади заданного участка карты, построению продольных профилей по заданным линиям. Для каждого типа задач даны примеры решения с подробными пояснениями.

Табл. - . Ил. 14.

 М. М. Орехов, А. Н. Соловьев,

Т. Ю. Терещенко, А. В. Волков. 2016

 Санкт-Петербургский государственный

архитектурно-строительный университет, 2016

Введение

Методические указания предназначены для выполнения расчетно-графической работы студентами всех форм обучения по направлениям «Строительство», «Архитектура», «Землеустройство и кадастры».

К основным целям расчетно-графической работы относятся:

1. 
   Закрепление теоретических и практических знаний, полученных студентами на лекциях, лабораторных и практических занятиях, а также в ходе самостоятельного изучения учебного материала с использованием топографических карт и планов;
   
2. 
   Формирование общепрофессиональных и профессиональных компетенций;
   
3. 
   Оценка уровня подготовки студентов.
   

---

1. 
   Исходные данные для выполнения
   

расчетно-графической работы
Расчетно-графическая работа выполняется на учебной топографической карте с номенклатурой У-34-37-В-в-4, масштаба 1:10 000.

Исходные данные для выполнения работы берутся студентом из приложения по номеру варианта, который указывается преподавателем.

К исходным данным относятся:

• 
  Сокращенные прямоугольные координаты исходной точки А – x_А и y_А;
  
• 
  Дирекционный угол с точки А на точку В – _АВ;
  
• 
  Расстояние от точки А до точки В – D_АВ;
  
• 
  Геодезические координаты точки С – B_Си L_С;
  
• 
  Заданная величина уклона с точки А на точку В – i_з;
  
• 
  Координаты участка местности;
  

Расчетно-графическая работа выполняется на листах бумаги формата А4, на которых производятся соответствующие вычисления, расчеты, вычерчиваются рисунки, схемы и т. д. Ситуация с топографической карты и результаты решения задач переносится на кальку или ксерокопию ее фрагмента. Записи выполняются аккуратно, без исправлений и подчисток. Схемы и все построения на выполняются остро заточенным карандашом. Все листы расчетно-графической работы должны быть скреплены и оформлены в соответствии с принятыми правилами.

При выполнении расчетно-графической работы необходимо решить следующие задачи:

1. По известным сокращенным прямоугольным координатам нанести точку А на топографическую карту и найти:

• 
  полные прямоугольные координаты – x_А и y_А;
  
• 
  геодезические координаты – В_А и L_А;
  
• 
  абсолютную высоту точки А – Н_А.
  

2. По известным полярным координатам нанести точку В на топографическую карту и определить:

• 
  сокращенные прямоугольные координаты точки В – x_В и y_В;
  
• 
  абсолютную высоту точки В – Н_В;
  
• 
  среднюю величину уклона линии АВ в промилле – i ‰;
  
• 
  значение истинного азимута А_АВ направления АВ.
  

3. По заданным геодезическим координатам точки С нанести точку С на топографическую карту и определить:

• 
  сокращенные прямоугольные координаты – x_А и y_А
  
• 
  абсолютную высоту точки С – Н_С;
  
• 
  расстояние между точками B и С – D_ВC;
  
• 
  расстояние между точками А и С – D_АC;
  
• 
  дирекционные углы направлений α_АС и α_ВС;
  
• 
  магнитный азимут направления BC – А_{М ВC} (на год решения расчетно-графической работы).
  

---

4. Построить линию заданного уклона i_з с точки А на точку В.

5. Дать топографическое описание участка местности, соответствующего заданным квадратам.

6. Обозначить на ксерокопии фрагмента топографической карты, в пределах района ограниченного точками А, В, С, водораздельные линии и тальвеги. Водораздельные линии показать коричневым или красным цветом, тальвеги зеленым или синим.

7. Вычислить графически и аналитически площадь участка местности, ограниченного его вершинами А, В, С – S м².

8. Построить продольный профиль земной поверхности по линии AB. Горизонтальный масштаб – 1:2000. Вертикальный масштаб – 1:200.
2. Методические рекомендации по выполнению расчетно-графической работы
Задача 1
По известным сокращенным прямоугольным координатам нанести точку А на топографическую карту и найти:

• 
  полные прямоугольные координаты – x_А и y_А;
  
• 
  геодезические координаты – В_А и L_А;
  
• 
  абсолютную высоту точки А – Н_А.
  

Для нанесения точки А на топографическую карту необходимо отыскать квадрат, образованный линиями координатной сетки карты, значения которых соответствуют заданным координатам в километрах. Положение точки А, показанное на рис. 1, внутри найденного квадрата определяют путем откладывания по осям x и y с помощью циркуля-измерителя или линейки отрезков l_х и l_у, длины которых соответствуют оставшемуся числу метров, выраженному в масштабе карты.

Для определения полных прямоугольных координат точки А по осям абсцисс и ординат определяют значение координатных линий сетки карты, соответствующие целому числу сотен километров, относительно которых определялись сокращенные координаты точки. Число сотен километров подписано мелким шрифтом около ближайших к углам рамки карты координатных линий. Найденные значениям сотен километров суммируют с значениями сокращенных координаты точки. Кроме того, к координате y приписывают слева значение номера зоны.

Пример. Нанести на топографическую карту точку А по ее сокращенным координатам и найти ее полные прямоугольные координаты (см. рис.1).

Дано: x_А = 66 785.0; y_А= 11 835.0.

Решение: Для масштаба 1:10 000 1см на карте соответствует 100 м на местности, поэтому l_х= 785:100 = 7.85 см и l_у = 835:100 = 8.35 см. Откладываем соответствующие значения от линий координатной сетки, и ставим точку

---

А.

Полные прямоугольные координаты соответствуют значениям x_А = 6 066 785.0 м; y_А = 4 311 835.0 м.

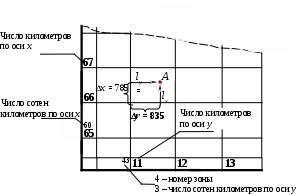
Рис. 1. Нанесение точки А на фрагмент топографической карты по прямоугольным координатам
Геодезические координаты точки А определяют от ближайших к ней линий меридиана и параллели, широта и долгота которых подписана в углах внутренней рамки топографической карты. Между внутренней и внешней рамками топографической карты расположена шкала, на которой показаны выходы меридианов и параллелей через одну минуту и через 10 секунд.

Для определения геодезических координат опускают перпендикуляры из точки А на западную (восточную) и южную (северную) стороны рамки карты. Искомые значения широты и долготы считываются в точках пересечения перпендикуляров с соответствующими сторонами рамки карты, по минутной и секундной шкале.


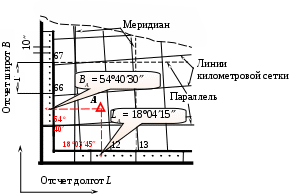
Рис. 2. Определение геодезических координат точки А
Абсолютная высота точки А по топографической карте может быть определена относительно горизонталей или подписанных отметок высот. На рис. 3 показаны эти способы.

Порядок определения абсолютной высоты относительно горизонталей следующий:

1. 
   найти на карте ближайшую к точке А основную горизонталь с надписью ее значения;
   
2. 
   определить высоту сечения рельефа (подписывается под южной рамкой топографической карты) и направление ската;
   
3. 
   рассчитать отметки горизонталей, между которыми располагается точка А;
   
4. 
   измерить величину заложения d между этими горизонталями и расстояние l от одной из них до определяемой точки А;
   
5. 
   в соответствии с полученными результатами рассчитать значение абсолютной высоты точки А.
   

Порядок определения абсолютной высоты относительно подписанных отметок высот следующий:

6. 
   найти на карте ближайший к точке А топографический объект с указанной абсолютной высотой (пункты государственной геодезической сети, нивелирные знаки, отметки урезов воды и т.д.);
   
7. 
   учитывая высоту сечения рельефа и направление ската, определить отметку ближайшей к этому топографическому объекту основной горизонтали;
   
8. 
   выполнить пункты в, г, д.
   

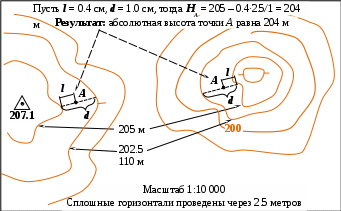
Рис. 3. Способы определения абсолютной высоты точки А

Задача 2
По известным полярным координатам нанести точку

---

В на топографическую карту и определить:

• 
  сокращенные прямоугольные координаты точки В – x_В и y_В;
  
• 
  абсолютную высоту точки В – Н_В;
  
• 
  среднюю величину уклона линии АВ в промилле – i ‰;
  
• 
  значение истинного азимута А_АВ направления АВ.
  

Для нанесения точки В на карту по заданным полярным координатам необходимо произвести следующие построения.

Через точку А, являющуюся полюсом для системы полярных координат, проводят вертикальную линию параллельно линии координатной сетки топографической карты – полярную ось. Относительно полярной оси, из полюса, с помощью транспортира, откладывают заданный угол положения или дирекционный угол _АВ, показанный на рис. 4, а и проводят луч, на котором откладывают радиус-вектор, соответствующий горизонтальному проложению заданного расстояния (рис. 4, б). Для этого, необходимо выбранное из таблицы исходных данных расстояние D_АВ, выразить в масштабе карты.



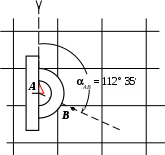
Рис. 4а. Построение заданного угла положения



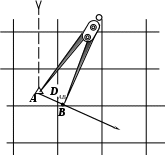
Рис. 4б. Построение заданного радиус-вектора

Пример. Нанести точку В на топографическую карту масштаба 1:10 000.

Даны полярные координаты точки В. Угол положения равен 112˚ 35′. Горизонтальное проложение D_АВ = 850 м.

Решение: С помощью транспортира откладывают заданный угол и проводят луч. Для масштаба 1:10 000 в 1 мм 10 м, тогда радиус-вектор равен 850 : 10 = 85 мм. С помощью циркуля-измерителя найденную величину откладывают по линии построенного направления и обозначают точку В.

Наклон линии местности АВ (рис. 5)характеризуется углом наклона линии и находится через тангенс этого угла, который называют уклоном.



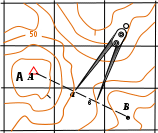
Рис. 5. Измерение заложения на топографической карте
Величину угла наклона определяют по графику масштаба заложений. Масштаб заложений помещается под южной стороной рамки топографической карты (рис. 6) и дается обычно для двух высот сечений: один для заложений между основными горизонталями, а другой между утолщенными, в случае, если, горизонтали располагаются очень плотно. На рис. 6 величина угла наклона равна 2.5.


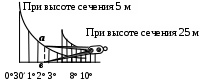
Рис. 6. Масштаб заложений на топографической карте масштаба 1:50 000

---

Смотрите также файлы

• Практическая работа 4 По дисциплине Информационная безопасность и защита информации.docx

• Ос это программа, запускающаяся сразу.docx

• Психология восприятия.docx

• Семинарскопрактическое занятие 5 по темам Ощущение и восприятие.docx

• В единицах времени.doc