Уклон линии вычисляют по формуле:

i = tgv = h/d, (1)

где i – уклон; v– угол наклона; h – высота сечения рельефа, м; d – заложение, м.

Для определения средней величины уклона линии АВ (рис. 6), проходящей через несколько горизонталей используют формулу:

i = [(Н_В– Н_А)/D_АВ] ∙ 1000, (2)

где i – уклон; (Н_В– Н_А) – разность высот точек А, В м; D_АВ – горизонтальное положение, м.

Уклон обычно выражают в тысячных (промилле) ‰.

Углы ориентирования отсчитывают от северного направления соответствующей линии по ходу часовой стрелки до заданного направления. На рис. 7 показана схема таких углов ориентирования до направления АВ. Угол ориентирования, отсчитываемый от меридиана, называют азимутом (истинным азимутом) А, от северного конца магнитной стрелки – магнитным азимутом А_м, от северного направления вертикальной линии километровой сетки – дирекционным углом α.

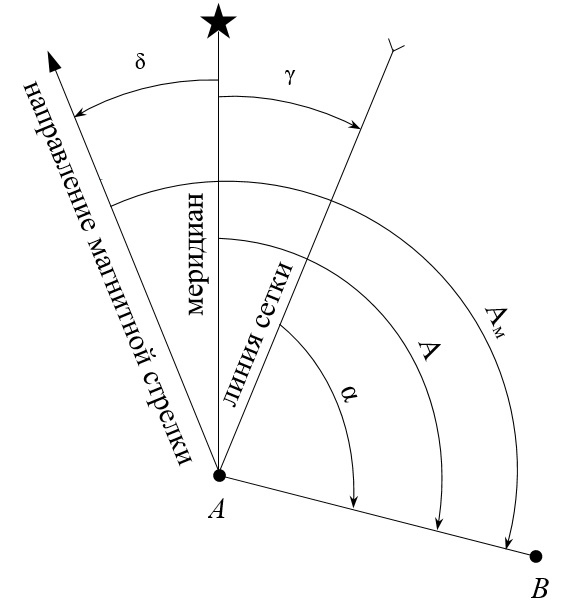
Рис. 7. Схема углов ориентирования линии АВ
Угол между северным направлением меридиана и магнитной стрелки называют склонением магнитной стрелки и обозначают δ. Если северный конец магнитной стрелки откланяется к востоку от меридиана, склонение магнитной стрелки будет восточным (положительным), а если к западу, то западное (отрицательное).

Угол между северным направлением меридиана и северным направлением вертикальной линии километровой сетки называют сближением меридианов γ. Если северный конец линии сетки откланяется к востоку от меридиана, сближением меридианов будет восточным (положительным), а если к западу, то западное (отрицательное).

Угол между северным направлением вертикальной линии километровой сетки и направлением магнитной стрелкой называют отклонением магнитной стрелки (поправкой направления) П. Отсчитывается от северного направления вертикальной линии километровой сетки. Если северный конец магнитной стрелки откланяется к востоку от вертикальной линии километровой сетки, поправка будет положительная, а если к западу, то отрицательная.

Азимут с магнитным азимутом выражен через формулу:

А = А_м + δ, (3)

где А – азимут; Ам – магнитный азимут; δ – склонение магнитной стрелки.

Азимут с дирекционным углом выражен через формулу:

А = α + γ, (4)

где А – азимут; α – дирекционный угол; γ – сближение меридианов.

---

Измеренный на местности магнитный азимут направления связан с дирекционным углом этого направления формулой:

А_м = α – П, (5)

где А_м – магнитный азимут; α – дирекционный угол; П – поправка направления.

Чтобы избежать ошибок при определении величины и знака поправки направления, целесообразно пользоваться помещаемой на топографических картах схемой взаимного расположения линий исходных направлений, показанной на рис. 8.


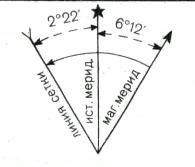
Рис. 8. Схема взаимного расположения линий исходных направлений
Задача 3
По заданным геодезическим координатам точки С нанести точку С на топографическую карту и определить:

• 
  сокращенные прямоугольные координаты – x_А и y_А
  
• 
  абсолютную высоту точки С – Н_С;
  
• 
  расстояние между точками B и С  D_ВС;
  
• 
  расстояние между точками А и С – D_АС;
  

• 
  дирекционные углы направлений α_АС и α_ВС;
  
• 
  магнитный азимут направления BC – А_{М ВC} (на год решения расчетно-графической работы).
  

Измерение расстояние между точками на топографической карте (плане) выполняется одним из двух способов.

1. С помощью линейки с миллиметровыми делениями и численного масштаба.

Для этого измеренное на карте (плане) расстояние в сантиметрах, умножают на знаменатель численного масштаба в метрах (величину масштаба).

Например, если на топографической карте масштаба 1: 10 000 расстояние между двумя точками равно 4.7 см, то на местности оно будет равно 4.7 × 100 = 470 м.

2. С помощью циркуля-измерителя и линейного масштаба.

Циркулем-измерителем берут раствор, соответствующий расстоянию АС на топографической карте и переносят на линейный масштаб. При этом правая ножка циркуля устанавливается в начало отсчета, а относительно левой снимают отсчет (рис. 9).


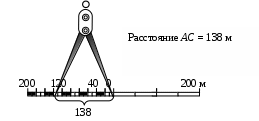
Рис. 9. Измерение расстояний с помощью линейного масштаба

Для определения магнитного азимута направления BC – А_{М ВC} на год решения расчетно-графической работы применяют следующий порядок.

1. Определяют значение магнитного склонения  на год решения расчетно-графической работы, например, 2016 г. Для этого высчитывают количество лет – n, прошедшее с момента измерения склонения: 2016 – 1971 = 45 лет.

---

2. Вычисляют, величину изменения магнитного склонение за прошедшие 45 лет. Для этого количество лет умножают на годовое изменение магнитного склонения:

 = n  _{1 год}:

 = 45  (+ 0°02') = + 1° 30'

3. Рассчитывают магнитное склонение на 2016 год:

₂₀₁₆ = ₁₉₇₁ + 

₂₀₁₆ = 6° 12' + 1° 30' = + 7° 42'

4. Определяют значение поправки направления – П:

П = ( )  ( ) = + 7° 42' – ( 2° 22') = + 10° 04'

5. По значениям поправки направления и величине дирекционного угла _АВ, вычисляют магнитный азимут этого направления: А_м =   ( П) = 112˚ 35′  10° 04' = 102˚ 31′
Задача 4
При построении линии заданного уклона i_з с точки А на точку В необходимо:

1. 
   Перенести ситуацию на кальку или сделать ксерокопию указанного участка топографической карты (плана).
   
2. 
   Определить, расчетную величину заложения d_расч, при котором уклон линии на данном участке местности будет равен заданному уклону i_з.
   
3. 
   На линии AB выделить участки, для которых величины заложения d > d_расч, т. е. |i| < i_з (участки «вольного хода») и участки, для которых величины заложения d ≤ d_расч, т. е. |i| > i_з (участки «напряженного хода»).
   
4. 
   На участке «напряженного хода» построить на кальке линию заданного уклона, т. е. линию, вдоль которой уклон местности удовлетворяет условию |i| =i_з.
   

Нанося на кальку линию заданного уклона, следует стремиться к тому, чтобы она не имела бы пилообразной формы (резко не меняла направление при пересечении с горизонталями) (рис. 10). ab = bc = cd = de = d_расч Из выражения (1): d_расч = h : i (‰).

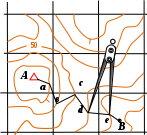
Рис. 10. Построение линии заданного уклона
Пример. Построить линии заданного уклона i_з на топографической карте масштаба 1:10 000.

Дано: i_задан = 21 ‰; h = 2.5 м.

Решение: Найдем величину заложения d_расч для заданного уклона:

d_расч = 2.5 : 0.021 = 119 м

В масштабе карты 1:10 000 это значение будет равно отрезку на карте равному 1.19 см = 119 : 100.

Полученное заложение берем в раствор циркуля и укладываем между смежными горизонталями, начиная от исходной точки.

---

Задача 5
Для выполнения топографического описания участка местности, соответствующего заданным квадратам, вначале изучают заданный участок по топографической карте. Обозначение участка местности задается сочетанием подписей километровых линий координатной сетки, образующих юго-западный угол квадрата. Например, квадрат 6512 с юга ограничен линией 65, с запада линией 12.

Описание участка местности выполняется в произвольной форме и должно отражать топографическую ситуацию. Для этого в описании указывают все местные предметы, их характеристики и взаимное расположение. Порядок описания должен соответствовать содержанию, представленному в условных знаках для топографической карты масштаба 1:10 000 и включать:

• 
  геодезические пункты, их вид и отметки;
  
• 
  населенные пункты и отдельные строения, их тип, количество жителей, число домов, огнестойкость построек, выдающиеся строения;
  
• 
  промышленные, сельскохозяйственные и социально-культурные объекты;
  
• 
  железные дороги и сооружения при них с основными характеристиками;
  
• 
  шоссейные и грунтовые дороги, их тип, размеры проезжей части и вид покрытия, выемки и насыпи;
  
• 
  гидрографию;
  
• 
  объекты гидротехнические и водного транспорта;
  
• 
  объекты водоснабжения;
  
• 
  мосты и переправы;
  
• 
  рельеф;
  
• 
  растительность;
  
• 
  основные сельскохозяйственные угодья;
  
• 
  грунты и микроформы земной поверхности;
  
• 
  болота и солончаки;
  
• 
  границы и ограждения.
  

Задача 6

Обозначить на ксерокопии фрагмента топографической карты, в пределах района ограниченного точками А, В, С, водораздельные линии и тальвеги. Водораздельные линии показать коричневым или красным цветом, тальвеги зеленым или синим.

При выполнении задачи следует руководствоваться тем, что линия, разделяющая сток атмосферных вод по двум склонам, направленным в разные стороны, называется водоразделом, а линия по дну, к которой направлены скаты и которая соединяет низшие точки, самые глубокие части дна – тальвегом.

На рис. 11 показан пример построения водораздельных линий и тальвегов.



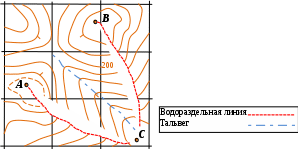
Рис. 11. Построение водораздельных линий и тальвегов

---

Задача 7

Вычислить графически и аналитически площадь участка местности, ограниченного его вершинами А, В, С – S м².

В зависимости от формы участка местности, технического оснащения и требуемой точности, площадь этого участка, изображенного на карте, может быть вычислена одним из способов:

• 
  подсчетом квадратов координатной сетки, покрывающих этот участок. Каждый квадрат, образуемый линиями координатной сетки на карте масштаба 1:10 000, соответствует на местности 1 км²;
  
• 
  графическими методами с использованием палеток или разбиением участка на простые геометрические фигуры;
  
• 
  аналитическими методами по координатам вершин участка местности;
  
• 
  методами, использующие современные компьютерные технологии.
  

Палетки для определения небольших участков с криволинейными границами обычно изготовляют на прозрачном материале, таком как, пластик, восковка, лавсан (рис. 12). На материал наносят сетку квадратов размером, как правило, 2×2 мм. Тогда такая палетка называется квадратная. Если наносят параллельные линии, палетку называют параллельной. Наложив квадратную палетку на план, подсчитывают число квадратов, уместившихся в измеряемой площади, оценивая неполные квадраты приближенно и считают площадь по формуле:

S = S_кв  n, (6)

где S_кв –площадь одного квадратика палетки; n – число квадратиков палетки, в пределах площади участка.

При определении площади по параллельной палетке, отрезки линий палетки, ограниченные контуром участка, рассматривают как средние линии трапеций – а_i. Измерив длины средних линий а₁ + а₂ + а₃ + а₄ ... циркулем-измерителем находят площадь по формуле:

, (7)

где h – расстояние между линиями палетки, выраженное в масштабе карты, а_i – длина отрезка палетки, ограниченного контуром участка.

При вычислениях необходимо не забывать о соответствии размеров на карте к размерам на местности в соответствии с масштабом карты.

Рис. 12. Квадратная и параллельная палетки
Площадь участка местности, если известны координаты его вершин

---

Смотрите также файлы

• Практическая работа 4 По дисциплине Информационная безопасность и защита информации.docx

• Ос это программа, запускающаяся сразу.docx

• Психология восприятия.docx

• Семинарскопрактическое занятие 5 по темам Ощущение и восприятие.docx

• В единицах времени.doc