Файл: Планконспект урока Применение производной для исследования функций Технологическая карта урока.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 19
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Сумарокова Лилия Зуфаровна
Учитель математики
ГОУ РК «ФМЛИ»
Республика Коми, г.Сыктывкар
План-конспект урока
Применение производной для исследования функций
Технологическая карта урока
Урок с применением исследовательских технологий
Ф.И.О. Сумарокова Лилия Зуфаровна
Предмет: математика модуль Алгебра
Класс: 10
Тип урока: Урок ОНЗ
| Тема | Применение производной для исследования функций |
| Цель урока | Организовать деятельность учащихся, направленную на овладение системой математических знаний и умений по теме «Применение производной для исследования функций», необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования. |
| Задачи | Образовательные: создать условия для актуализации знаний об исследовании функции, о производной. Обеспечить в ходе урока создание и усвоение алгоритма исследования функции с помощью производной. Развивающие: создать условия для развития коммуникативных навыков, внимания, анализа, формирования самостоятельной познавательной деятельности. Воспитательные: повышение уровня мотивации и интереса к математике |
| УУД |
|
| Планируемые результаты | Предметные: Знание алгоритм исследования функции с помощью производной Умение исследовать функцию с помощью производной, читать график функции Личностные: Формирование устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивать результаты своей учебной деятельности и других учеников, осознавать социальную роль ученика, проявлять положительное отношение к урокам математики, давать оценку и самооценку результатам учебной деятельности. Метапредметные: Умение решать проблемы творческого и поискового характера |
| Основные понятия | Функция, производная, исследование функции, график |
| Межпредметные связи | Геометрия, русский язык |
| Ресурсы | Презентация, тетрадь, учебник Алгебра и математический анализ 10 класс, проектор и компьютер, листы самооценки |
| Формы урока | Г – групповая, И – индивидуальная |
| Технология | Исследовательская, проблемная, информационно-коммуникационная, здоровьесберегающая |
| Дидактическая структура урока | Деятельность учеников | Деятельность учителя | Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов | Планируемые результаты | ||||
| Предметные | УУД | |||||||
| личностные | познавательные | коммуникативные | регулятивные | |||||
| Мотивация Время: 3 мин. | Приветствуют учителя. Проверяют себя: все ли у них готово к уроку. Включаются в учебную деятельность. Слушают и отвечают на вопросы, осмысливают проблему. | Приветствует детей. Заинтересовывает детей вопросом: «Готовы ли вы сегодня решить одну из задач ЕГЭ с использованием производной?» Проверяет готовность детей к уроку. Задает вопросы, организует работу по осмыслению проблемы, мотивирует учащихся, побуждая к деятельности по ее решению. | Задание на Слайде 1: №1. (Задание ЕГЭ по математике). По графику функции 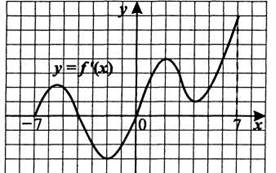 1. Сколько точек максимума имеет эта функция? 2. Назовите точки минимума функции. 3. Сколько промежутков возрастания у этой функции? 4. Найдите длину промежутка убывания | Знать и уметь применять алгоритм исследования функции при чтении графика. | Мотивация на учебный процесс. Действие смыслообразования | Анализируют предложенное задание. Строят речевое высказывание. | Высказывают свою точку зрения, слушают собеседника, учителя. | Волевая саморегуляция. Соотносят свои знания о поведении функции с ее графиком, встают перед проблемой недостаточности своих знаний для ответа на группу вопросов со слайда №1 |
| Актуализация субъективного опыта Время: 3 мин. | Отвечают, слушают ответы других Вспоминают алгоритм исследования, отвечают на вопросы. Формулируют алгоритм. Осуществляют взаимопроверку. Формулируют тему урока. | «Итак, ребята! Мы с вами встали перед проблемой, которая возникает на экзамене перед человеком, который не знает о связи поведения функции в зависимости от производной. Поднимите руки: кто умеет читать графики функций?» «Молодцы! Давайте проверим ваши умения». «Кто может рассказать полный алгоритм исследования функции?» «Ребята, кто может сформулировать тему урока?» Обсуждает варианты названия темы с учащимися и озвучивает тему урока «Исследование функции с помощью производной». | Слайде 2. №2. По графику функции 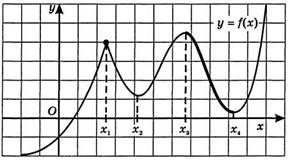 1. Сколько точек максимума имеет эта функция? 2. Назовите точки минимума функции. 3. Сколько промежутков возрастания у этой функции? 4. Назовите наименьший из промежутков убывания этой функции. | Знать и уметь проводить исследование функции по ее графику. | Слушают учителя, строят понятные для собеседника высказывания | Извлекают необходимую информацию Выдвигают предположения Анализируют, сравнивают, обобщают материал | Учитывают разные мнения Развивают навыки сотрудничества и управления эмоциями. | Принимают и сохраняют учебную цель и задачу, |
| Восприятие и осмысление учащимися нового материала Время: 10 мин. | По данным графикам функции и ее производной обсуждают и исследуют в парах поведение функции и ее производной, письменно отвечая на вопросы учителя, предложенные в карточках. | Исследовательская работа в парах | 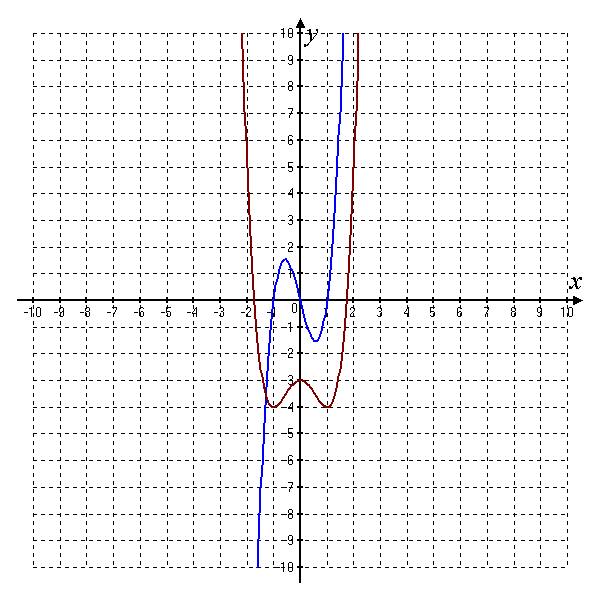
Если Если
Если Если функция Если функция | Применять исследовательские навыки при решении задач. | Мотивация на учебный процесс. | Извлекают необходимую информацию, анализируют текст. Осуществляют знаково-символическое моделирование. выбирают наиболее эффективных способов решение задачи в зависимости от конкретных условий. | Участвуют в обсуждении, | |
| Первичная проверка понимания Время: 4 минуты | Представители групп представляют результаты своей исследовательской деятельности. В ходе обсуждения составляют алгоритм исследования непрерывной функции на монотонность и экстремумы, записывают его в тетрадь. | Учителю в ходе обсуждения выводов учащихся, необходимо отметить: для того, чтобы исследовать функцию на монотонность и экстремумы, необязательно строить график производной, достаточно определить знаки производной на промежутках, на которые стационарные и критические точки разбивают область определения функции. Фактически | Алгоритм исследования функции с помощью производной.
| Уметь проговаривать алгоритм исследования функции с помощью производной и применять его при решении задач. | | Строят речевое высказывание. Анализируют, сравнивают, делают выводы, строят доказательство. | Выражают свои мысли в соответствии с задачами | Определяют последовательность действий при исследовании функции. |
| Первичное закрепление Время: 6 минут | Учащиеся в парах обсуждают задание и выполняют его. После выполнения задания обсуждают полученные результаты. | Учитель дает задание на карточке. «Молодцы, ребята! А теперь ответьте на вопросы в карточках, применяя полученный алгоритм». Организует самостоятельное выполнение пробного учебного действия. Заслушивает ответы учащихся, задает уточняющие вопросы. Организует фиксацию индивидуальных затруднений в выполнении учащимися пробного учебного действия или в его обосновании. | №1. Непрерывная функция 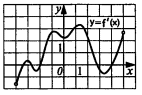 На рисунке изображён график её производной. Укажите количество промежутков возрастания функции. Укажите количество точек графика этой функции, в которых касательная параллельна оси Ох. №2. На рисунке изображен график функции 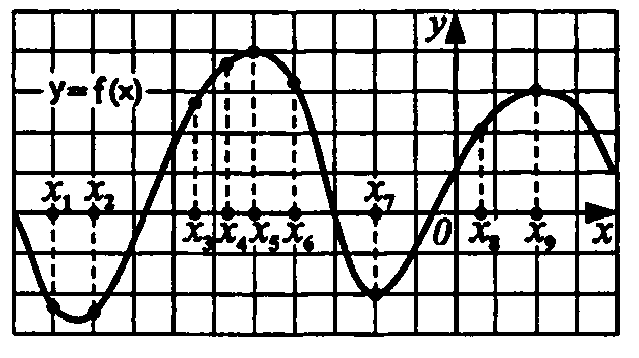 Найдите число отмеченных точек, в которых производная отрицательна (положительна). №3. На рисунке изображен график производной непрерывной функции 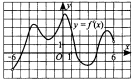 Назовите промежутки убывания функции. Назовите промежутки возрастания и выберите из них наибольший. Укажите число точек экстремума. | Решать задания на применение алгоритма с помощью графика. | | Умение осознанно и произвольно строить речевое высказывание и применять алгоритм. | Управление поведением партнера; умение выражать свои мысли. | Производят коррекцию способов действия, оценивают результаты действий |
| Включение в систему знаний Время: 9 минут | Самостоятельное выполняют пробное учебное действие. Задают уточняющие вопросы. Записываю в тетрадь решение по образцу. | Организует выявление типов заданий, где используется применение нового способа действия. По результатам выполнения самостоятельной работы организоует рефлексию деятельности по применению нового способа действия. | Задания из учебника для самостоятельной работы № 439, 441, 443, 445, 459, 461. | Знать алгоритм решения задач на исследование функции с помощью производной и уметь применять его при решении задач. | | Анализируют текст. Осуществляют знаково-символическое моделирование, выбирают наиболее эффективный способ решения задачи в зависимости от конкретных условий. | | Контроль в форме сличения способа действия и его результата с заданным эталоном, коррекция; оценивание качества и уровня усвоения. |
| Анализ Время: 3 минуты | Сравнивают ответы, размышляют. Делают вывод о разрешении проблемы. Отвечают на вопросы задачи. | Учитель заслушивает ответы учащихся и возвращает их к проблеме, поставленной в начале урока: «Можете ли вы теперь ответить на вопрос первой задачи? Какой вывод можно сделать?» | №1. (Задание ЕГЭ по математике). По графику функции  1. Сколько точек максимума имеет эта функция? 2. Назовите точки минимума функции. 3. Сколько промежутков возрастания у этой функции? 4. Найдите длину промежутка убывания. | | | Анализируют, сравнивают, делают выводы, строят доказательство | Высказывают свою точку зрения | Волевая саморегуляция. |
| Рефлексия Время: 2 минуты | Отвечают на вопросы, осуществляют самооценку. | «Каждый из вас сегодня на уроке занимался исследовательской деятельностью. Что вы получили в результате исследования? Где может пригодиться полученное вами знание?». Далее учитель предлагает заполнить таблицу: «Знаю, сомневаюсь, умею». | Таблица «Знаю, сомневаюсь, умею» | | Адекватно понимать причины успеха (неуспеха) в учебной деятельности. | Учатся структурировать знания, оценивать процесс и результаты деятельности. | Выражают свою точку зрения. | Оценка, выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня подготовки |