Файл: Практических заданий по дисциплине экономикоматематические методы и модели в логистике.docx
Добавлен: 09.11.2023
Просмотров: 58
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ В ЛОГИСТИКЕ
Группа ММ20М491
Студент
А.А. Липатов
МОСКВА 2023
Задача 1. У поставщиков А1, А2, А3 сосредоточено соответственно 80, 30, 50 единиц некоторого однородного груза. Этот груз необходимо доставить потребителям В1,В2,В3 в количестве 20, 60 и 80 единиц соответственно. Стоимость перевозок единицы груза от поставщиков к потребителям задается матрицей коэффициентов затрат
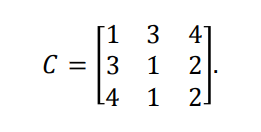
Необходимо построить первоначальный план поставок методом северозападного угла и вычислить их суммарную стоимость.
Необходимо построить первоначальный план поставок методом северозападного угла и вычислить их суммарную стоимость.
Решение :
Определим суммарную мощность поставщиков М=80+30+50=160
Определим суммарный спрос потребителей N=20+80+60=160
По сколько суммарная мощность равна Суммарному спросу то экономико-математическая модель транспортной задачи является закрытой.
Строим первоначальный план поставок
| | 20 | 60 | 80 |
| 80 | 1/20 | 3/60 | 4 |
| 30 | 3 | 1/0 | 2/30 |
| 50 | 4 | 1 | 2/50 |
| На основание таблицы производим расчет суммарной стоимости F=1*20+3*60+1*0+2*30+2*50=360 Практическое занятие 2. Задача 1. С помощью матрицы оценок исследовать на оптимальность план поставок 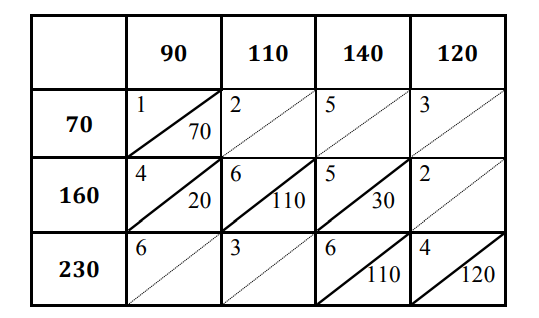 Решение
x11 = 0 = 0 + а + 1; а = -1 x21 = 0 = -1 + b+ 4; b = -3 x22 = 0 = -3 + c + 6; с = -3 x23 = 0 = -3 +d +5; d = -2 x33 = 0 = e + (-2) + 6; е = -4 x34 = 0 = -4 +f +4; f = 0 0-133 000-1 1-400 Поскольку матрица оценок содержит отрицательные числа, то план поставок не является оптимальным Задача 2 С помощью распределительного метода найти оптимальный план поставок, используя первоначальный план 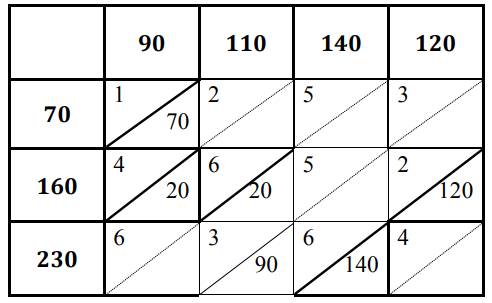 Решение:
x11 = 0 = 0 + а + 1; а = -1 x21 = 0 = b+ (-1) + 4; b = -3 x22 = 0 = -3 + c + 6; с = -3 x32 = 0 = -3 +d +3; d = 0 x33 = 0 = 0 + 6; е = -6 x24 = 0 = -3 +f 2; f = 1 используем цикл пересчета (2,3)-(3,3)-(3,2)-(2,2)-(2,3) Получаем таблицу
x11 = 0 = 0 + а + 1; а = -1 x21 = 0 = b + (-1) + 4; b = -3 x23 = 0 = -3 + е + 5; е = -2 x24 = 0 = -3 +f +2; f= 1 x33 = 0 = -2+ d+ 6; d = -4 x32 = 0 = -4 +c+3; c = 1 Формируем матрицу : 0334 0400 1001 Полученная матрица оценок указывает на то, что новый план поставок является оптимальным Вычислим значение целевой функции для транспортной задачи по формуле F=1*70+4*20+6*20+2*120+3*90+6*140=70+80+120+240+270+840=1620. |