Лабораторная работа (вариант 34)Определение коэффициента вязкости жидкости методом СтоксаЦель работы: изучение явления внутреннего трения в жидкостях и опытное определение величины коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке.Приборы и принадлежности: цилиндрический сосуд с исследуемой жидкостью, штангенциркуль, секундомер, масштабная линейка, шарики. Виртуальная установка.Теоретическая частьЯвлением внутреннего трения (вязкости) называется появление сил трения между слоями жидкости (или газа) движущимися друг относительно друга параллельно и с разными по величине скоростями.Т 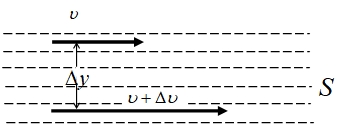урбулентным называется такое течение жидкости, при котором её частицы совершают неустановившееся и неупорядоченные движения по сложным траекториям, приводящим к перемешиванию слоёв. Ламинарное – это упорядоченное течение жидкости, при котором траектории движения соседних частиц мало отличаются друг от друга. 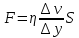При ламинарном течении жидкость можно рассматривать как совокупность отдельных слоёв, движущихся с различными скоростями.При движении плоских слоев сила трения между ними согласно закону Ньютона равна: где 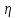- коэффициент пропорциональности, называемый коэффициентом вязкости или динамической вязкостью; - площадь соприкосновения слоев, 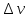- разница в скорости между соседними слоями, 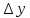- расстояние между соседними слоями.Отсюда 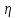численно равен тангенциальной силе, приходящейся на единицу площади соприкосновения слоев, необходимой для поддержания разности скоростей, равной единице,

---

между двумя параллельными слоями вещества, расстояние между которыми равно единице. В СИ единица вязкости - .

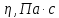Пусть в заполненном жидкостью сосуде движется шарик, размеры которого значительно меньше размеров сосуда. На шарик действуют три силы: сила тяжести 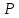, направленная вниз; сила внутреннего трения 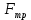и выталкивающая сила 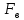, направленные вверх. Шарик сначала падает ускоренно, но затем очень быстро наступает равновесие, так как с увеличением скорости растет и сила трения. Стокс же показал, что эта сила при малых значениях скорости пропорциональна скорости движения шарика 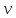и его радиусу 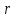: 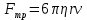,  где - коэффициент вязкости.

Описание экспериментальной установки

Н 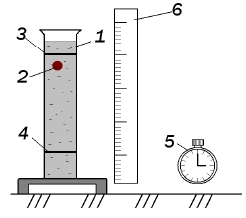а цилиндре имеются метки 3 и 4. Расстояние между метками L можно замерить при помощи линейки 6, а диаметр шарика – при помощи микрометра. Время прохождения между метками 3 и 4 можно определить с помощью секундомера 5. Метка 3 помещена на несколько сантиметров ниже верхнего уровня жидкости для выполнения условия равномерного движения шарика в жидкости; V = const на участке L. Цилиндр закрыт пробкой с воронкой, в которую опускается шарик, двигающийся в дальнейшем примерно по оси цилиндра так, чтобы на его движение не влияли стенки. При более точных измерениях необходимо учитывать влияние размеров стеклянного цилиндра.

Исследуемой жидкостью является глицерин

---

, плотность которого

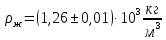- плотность глицерина

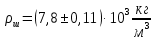- плотность стальных шариков

Эксперимент можно проводить как на физической, так и на виртуальной модели установки.

Основные расчетные формулы

1. 
   Сила трения:
   

где - коэффициент вязкости, - радиус шарика, - скорость движения шарика;

2. 
   Сила тяжести:
   

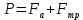
где - сила тяжести, действующая на шарик, 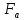- сила Архимеда, -сила внутреннего трения;

3. 
   Сила тяжести:
   

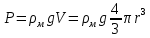
где 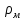- плотность материала шарика; 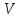– объем шарика;

4. 
   Сила Архимеда:
   

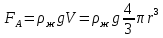
где 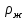- плотность жидкости;

5. 
   Число Рейнольдса:
   

6. 
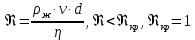
   Определение вязкости жидкости:
   

7. 
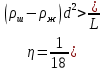
   Расчёт погрешностей косвенных измерений :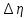
   

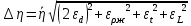
8. 
   Расчет абсолютной погрешности :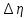
   

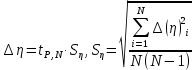
где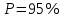- доверительная вероятность,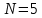

---

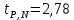
- число опытов, Экспериментальная часть

1. 
   Выполним экспериментальную часть задания и заполним таблицу 1 измерениями и вычислениями. Даны измерения:
   

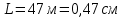, остальные значения в диапазоне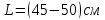 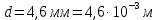, остальные значения в диапазоне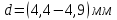 -плотность глицерина - плотность стальных шариковТаблица 1.Таблица измерений и вычислений

№
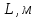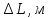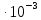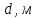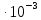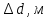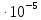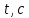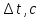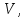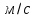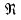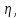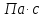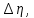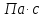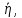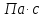1	0,45	5	4,4	5	9,7	0,1	0,046	0,17	1,49	-0,02	1,47
2	0,45		4,9		7,6		0,059	0,25	1,44	0,03
3	0,50		4,4		10,6		0,047	0,18	1,46	0,01
4	0,50		4,9		8,6		0,058	0,24	1,47	0
5	0,47		4,6		9,3		0,050	0,19	1,49	-0,02

---

2. 
   Вычислим скорость падения шарика для каждого опыта по формуле:
   

3. 
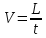
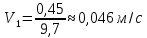
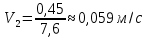
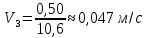
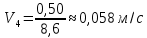
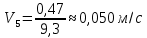
   Вычислим значение коэффициента вязкости для каждого опыта по формуле:
   

4. 
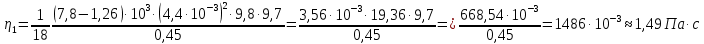
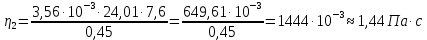
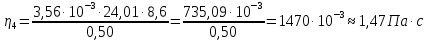
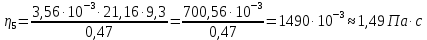
   Вычислим среднее значение коэффициента вязкости по формуле:
   

5. 
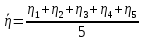
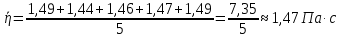
   Вычислим число Рейнольдса для каждого опыта по формуле:
   

6. 
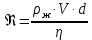
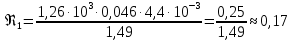
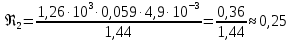
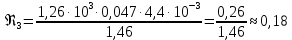
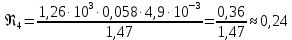
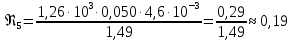
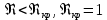
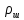   Определим абсолютные приборные погрешности прямых измерений (расстояния между метками , диаметра шарика , времени его падения , плотности шарика и жидкости ), а также их относительные ошибки ε_L, ε_d, и ε_t.
   

---

Смотрите также файлы

• Оптимизация управления товарными запасами на предприятии.docx

• Курсовая работа состоит из введения, двух глав, заключения, списка литературы.docx

• Ата аналар олхаты.docx

• Планконспект проведения занятия по предмету Пожарная тактика со слушателями курсов первоначального обучения пожарных.docx

• Планконспект проведения занятий с лc 2го дежурного караула псч4 3 псо по дисциплине Оказание первой помощи Тема Первая помощь при ранениях. Вид занятия Классногрупповое Отводимое время 1 (ч).doc