ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 78
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приборная погрешность
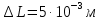
Приборная погрешность
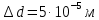
Приборная погрешность
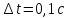
Приборная погрешность
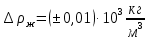 -плотность глицерина
-плотность глицеринаПриборная погрешность
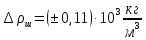 - плотность стальных шариков
- плотность стальных шариковОтносительная ошибка измерений:
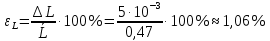
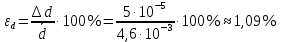
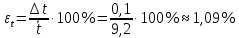
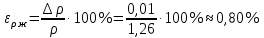
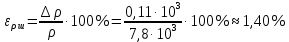
-
Оценим полную абсолютную и относительную
и относительную 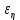 погрешности:
погрешности:
-
Рассчитаем с учетом доверительных погрешностей (коэффициента Стьюдента):
с учетом доверительных погрешностей (коэффициента Стьюдента):
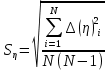
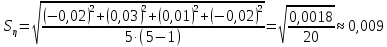
где
 - доверительная вероятность,
- доверительная вероятность,  - число опытов,
- число опытов,  ,
,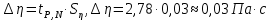
Искомая величина вязкости жидкости с учетом доверительных погрешностей:
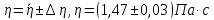
-
Рассчитаем по методике расчёта погрешностей косвенных измерений:
по методике расчёта погрешностей косвенных измерений:
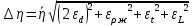
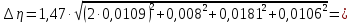
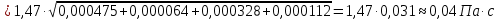
Искомая величина вязкости жидкости с учетом косвенных погрешностей:
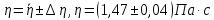
-
Вычислим относительную погрешность :
:
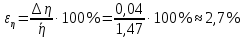
-
Сравним полученное значение со справочными данными.
со справочными данными.
В соответствии с табличными данными вязкость глицерина при температуре 20°С составляет 1,48 Па·с, что с учетом приборных погрешностей является измеряемой нами величиной равной
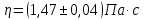 .
.Вывод: в ходе выполнения лабораторной работы были изучены явления внутреннего трения в жидкостях и экспериментально определена величина коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке. Путем постановки 5 опытов (для наибольшей точности) со стальными шариками (различного диаметра), удалось установить, что скорость шарика, движущегося в сосуде с жидкостью, зависит от размеров шарика. В результате получено среднее значение вязкости жидкости (глицерина)
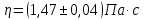 , с учетом погрешности
, с учетом погрешности 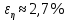 , что позволяет говорить о точности расчетной формулы и о незначительных приборных погрешностях при измерениях и вычислениях. Относительно табличных значений вязкости глицерина искомая величина вычислена верно и подтверждена экспериментально.
, что позволяет говорить о точности расчетной формулы и о незначительных приборных погрешностях при измерениях и вычислениях. Относительно табличных значений вязкости глицерина искомая величина вычислена верно и подтверждена экспериментально.Контрольные вопросы
-
Поясните сущность явления вязкого трения. Какова природа сил внутреннего трения жидкости?
Явлением внутреннего трения (вязкости) называется появление сил трения между слоями жидкости (или газа) движущимися друг относительно друга параллельно и с разными по величине скоростями.
Вязкость или внутреннее трение – свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Это явление определяет диссипацию (поглощение) энергии при деформации среды. При деформации сдвига вязкость называют сдвиговой. При деформации объема (всестороннее сжатие) проявляется объемная вязкость. В данном случае мы будем касаться только вопроса сдвиговой вязкости.
Суть явления состоит в том, что движущиеся слои газа или жидкости увлекают соседние слои и, наоборот, неподвижные (или движущиеся с меньшей скоростью) тормозят более быстрые соседние слои. Таким образом, между любыми соседними слоями рассматриваемой среды действуют силы внутреннего трения (или силы вязкости). Механизм возникновения этих сил заключается в переносе импульса (количества движения) от одного слоя к другому.
-
Что такое коэффициент динамической вязкости? В каких единицах измеряется величина вязкости в системе СИ?
в системе СИ?
Динамическая вязкость η (η= „Eta“) - это единица измерения вязкости или вязкотекучести жидкости. Чем выше значение параметра вязкость, тем более тягучая (вязкая) жидкость; чем меньше вязкость, тем он более жидкий (текучий).
Единица измерения динамической вязкости в СИ: [η] = Паскаль·секунду (Па·с) = Н·с/м² = кг/м·с
-
Какие силы действуют на тело, движущееся в жидкости?
На тело, погруженное в жидкость и остающееся в равновесии на плаву действуют две силы: сила тяжести и равная ей выталкивающая сила (и равная весу жидкости, вытесненной погруженным объёмом тела). На тело, погруженное в жидкость и тонущее действуют три силы: сила тяжести, неравная ей (меньше) выталкивающая сила (равная весу жидкости, вытесненной погруженным объёмом тела) , а также сила трения при движении, в значительной степени зависящая от скорости погружения и вязкости жидкости.

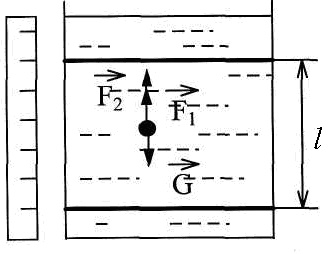
Рис.3
На тело, погруженное в жидкость и лежащее плотно на дне, действуют три силы: сила тяжести, неравная ей выталкивающая сила, и сила реакции со стороны дна. В данном случае выталкивающая сила уменьшается на величину, равную весу жидкости, занимаемому той частью объёма тела, под которой нет воды.
Предоставим маленькому шарику возможность падать в жидкость под действием силы тяжести. На него будут действовать следующие силы (рис.3):
1) Сила тяжести, направленная по вертикали вниз
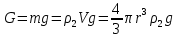 , где
, где 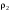 – плотность шарика, g - ускорение свободного падения.
– плотность шарика, g - ускорение свободного падения.2) Выталкивающая сила F1, являющаяся результатом гидростатического давления. Она направлена по вертикали вверх и равна по закону Архимеда силе тяжести жидкости в объеме тела:
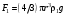 , где
, где 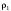 – плотность жидкости.
– плотность жидкости.3) Сила внутреннего трения F
2 . Она направлена против направления скорости шарика, т.е. вертикально вверх. По формуле Стокса:
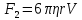
-
Дайте определение ламинарного и турбулентного течения жидкости.
Турбулентным называется такое течение жидкости, при котором её частицы совершают неустановившееся и неупорядоченные движения по сложным траекториям, приводящим к перемешиванию слоёв. Ламинарное – это упорядоченное течение жидкости, при котором траектории движения соседних частиц мало отличаются друг от друга.
-
Запишите формулу Стокса и укажите условия ее применимости.
Для тел сферической формы модуль силы вязкого трения определяется формулой Стокса:
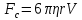
где r – радиус шарика; V – скорость его движения относительно жидкости. Важно отметить, что формула Стокса справедлива только в случае ламинарного течения жидкости относительно шарика (скорость движения шарика должна быть небольшой), а жидкость по всем направлениям простирается безгранично, т.е. размеры сосуда, в котором находится жидкость, должны быть много больше по сравнению с размерами шарика.
-
Определите величину силы трения, действующей на стальной шарик диаметром 3 мм, падающий со скоростью 0,75 м/с в жидкости с коэффициентом вязкости 1,5 Па.с.
По формуле Стокса рассчитаем:
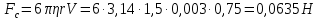
-
Почему шарик в начале движения ускоряется, а затем движется равномерно? Что такое градиент скорости?
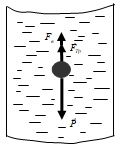 В начале движения шарика движение будет ускоренным за счет ускорения свободного падения. С ростом скорости растет и сила сопротивления, а ускорение шарика уменьшается. Наступает такой момент, когда действующие на шарик силы уравновесятся, ускорение станет равным нулю, а движение шарика - равномерным на участке L.
В начале движения шарика движение будет ускоренным за счет ускорения свободного падения. С ростом скорости растет и сила сопротивления, а ускорение шарика уменьшается. Наступает такой момент, когда действующие на шарик силы уравновесятся, ускорение станет равным нулю, а движение шарика - равномерным на участке L.Градиент скорости – это изменение скорости двух слоёв жидкости dV на расстоянии между слоями dL.
-
Запишите рабочую формулу, объясните условия её применения и причину начала измерения времени не от поверхности жидкости.
Формула определения коэффициента вязкости жидкости:

При явлении внутреннего трения (вязкости) появляются силы трения между слоями жидкости (или газа) движущимися друг относительно друга параллельно и с разными по величине скоростями. При движении плоских слоев сила трения между ними согласно закону Ньютона равна:
При движении плоских слоев сила трения между ними согласно закону Ньютона равна:

где
 - коэффициент пропорциональности, называемый коэффициентом вязкости или динамической вязкостью;
- коэффициент пропорциональности, называемый коэффициентом вязкости или динамической вязкостью;  - площадь соприкосновения слоев,
- площадь соприкосновения слоев,  - разница в скорости между соседними слоями,
- разница в скорости между соседними слоями,  - расстояние между соседними слоями.
- расстояние между соседними слоями.Отсюда
 численно равен тангенциальной силе, приходящейся на единицу площади соприкосновения слоев, необходимой для поддержания разности скоростей, равной единице, между двумя параллельными слоями вещества, расстояние между которыми равно единице. В СИ единица вязкости -
численно равен тангенциальной силе, приходящейся на единицу площади соприкосновения слоев, необходимой для поддержания разности скоростей, равной единице, между двумя параллельными слоями вещества, расстояние между которыми равно единице. В СИ единица вязкости -  .
.Пусть в заполненном жидкостью сосуде движется шарик, размеры которого значительно меньше размеров сосуда. На шарик действуют три силы: сила тяжести
 , направленная вниз; сила внутреннего трения
, направленная вниз; сила внутреннего трения  и выталкивающая сила
и выталкивающая сила  , направленные вверх. Шарик сначала падает ускоренно, но затем очень быстро наступает равновесие, так как с увеличением скорости растет и сила трения. Стокс же показал, что эта сила при малых значениях скорости пропорциональна скорости движения шарика
, направленные вверх. Шарик сначала падает ускоренно, но затем очень быстро наступает равновесие, так как с увеличением скорости растет и сила трения. Стокс же показал, что эта сила при малых значениях скорости пропорциональна скорости движения шарика  и его радиусу
и его радиусу  :
:  , где
, где  - коэффициент вязкости.
- коэффициент вязкости.