Файл: Курсовая работа Гидравлический расчет сложного трубопровода и элементов оборудования по дисциплине Гидравлика и нефтегазовая гидромеханика.docx
Добавлен: 09.11.2023
Просмотров: 108
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
 «Уфимский государственный нефтяной технический университет»
«Уфимский государственный нефтяной технический университет»Кафедра «Гидравлика и гидромашины»
Курсовая работа
«Гидравлический расчет сложного трубопровода
и элементов оборудования»
по дисциплине «Гидравлика и нефтегазовая гидромеханика»
Выполнил: студент гр. БМТ-12-04 ___________ А.А. Гибатов
(подпись, дата)
Проверил: ___________ Э.С.Бахтегареева
(подпись, дата)
Уфа 2014
-
 Задача № 1-10
Задача № 1-10
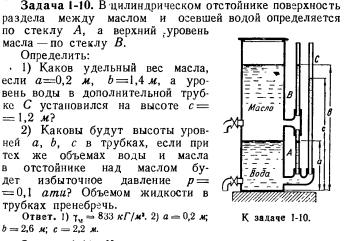
В цилиндрическом отстойнике поверхность раздела между маслом и осевшей водой определяется по стеклу А, а верхний уровень масла – по стеклу В.
Определить: 1) Каков удельный вес масла, если a=0.2 м, b= 1,4 м , а уровень воды в дополнительно трубке C установился на высоте с=1,2 м? 2) каковые будут высоты уровней a, b, c в трубках, если при тех же объемах воды и масла в отстойнике над маслом будет избыточное давление p=0.1 атм? Объем жидкости в трубах пренебречь.
Решение:
Плотность воды
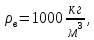
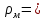 ?
?-
По основному закону гидростатики
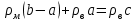
Отсюда:
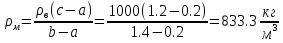
-
При P=10 кПа превышение уровня в трубе B над поверхностью масла в отстойнике по основному закону гидростатики составит:
P=
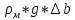 откуда
откуда 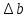 =10000/ 9.81*833.3=1.22 м
=10000/ 9.81*833.3=1.22 мУровень в трубке не изменится, так как давление на высоте a в отстойнике и трубке A одинаковы, т.е. a’=a=0.2 м.
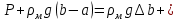
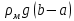
Следовательно новая высота :
b’=b+1.22==1.4+1.22=2.62 м.
высота c’ определяется из условия :
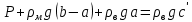
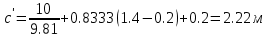
Ответ:
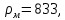 3
3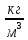 , a’=0.2 м., b’=2.62 м., c’=2.22 м.
, a’=0.2 м., b’=2.62 м., c’=2.22 м.Задача 2-18
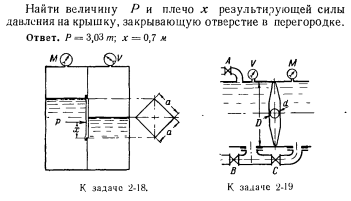
Замкнутый резервуар с нефтью разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной a=1 м. Давление над нефтью в левой части резервуара определяется показанием манометра M=0.15 кГ/
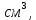 а в правой – показанием вакуумметра V=0.1 кГ/
а в правой – показанием вакуумметра V=0.1 кГ/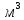 . Уровни нефти указаны на эскизе. Найти величину P и плечо x результирующей силы давления на крышку, закрывающую отверстие в перегородке.
. Уровни нефти указаны на эскизе. Найти величину P и плечо x результирующей силы давления на крышку, закрывающую отверстие в перегородке.Решение:
 Сила монометрического давления на перегородку приложена в центре тяжести перегородки и направлена слева направо
Сила монометрического давления на перегородку приложена в центре тяжести перегородки и направлена слева направо 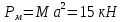 .
.Сила вакуумметрического давления жидкости на плоскую стенку
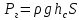 , где
, где 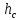 - расстояние от свободной поверхности жидкости до центра тяжести плоской поверхности площадью S.
- расстояние от свободной поверхности жидкости до центра тяжести плоской поверхности площадью S.  Точка приложения
Точка приложения 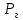 - центр давления.
- центр давления.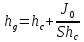 , где
, где 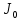 - центральный момент инерции.
- центральный момент инерции.Сила давления слева :
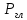 =9,81*0,92*a*
=9,81*0,92*a*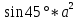 =9.81*0.92.0.707=6.38 кН
=9.81*0.92.0.707=6.38 кН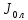 =
=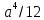 ;
; 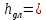 a*
a*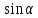
+
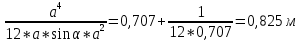
Сила давления справа :
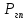 =9,81*0,92*0,707/6=1,063 кН
=9,81*0,92*0,707/6=1,063 кН 1/3*a*
1/3*a* +
+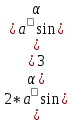 =0.295 м.
=0.295 м.Суммарная сила
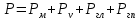 = 15+20+6,38-1,063=30,3 кН
= 15+20+6,38-1,063=30,3 кНРассмотрим схему сил и обозначим :
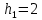 *a*
*a* -
- 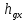 =2*0.707 – 0.825 = 0.585
=2*0.707 – 0.825 = 0.585 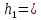 a*
a* -
- 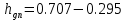 =0.472
=0.472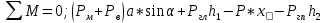 =0;
=0;x=
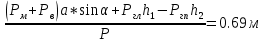
Ответ:
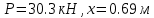
 2.2 Решение
2.2 Решение Данную схему можно разделить на 4 простых трубопровода, причем трубопровод 1 (
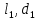 ) является всасывающим и рассчитывается отдельно от сложного, состоящего из трубы 2 (
) является всасывающим и рассчитывается отдельно от сложного, состоящего из трубы 2 (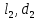 ), трубопровода 3 (
), трубопровода 3 (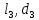 ), трубопровода 4 (
), трубопровода 4 (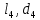 ).
).Запишем уравнение Бернулли:
Вых-E
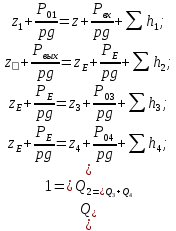
Где
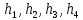 – потери напора в первом, втором, третьем и четвертом трубопроводе.
– потери напора в первом, втором, третьем и четвертом трубопроводе.Учитывая, что z=0 и
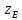 = 0 записываем уравнения Бернулли в новом виде :
= 0 записываем уравнения Бернулли в новом виде :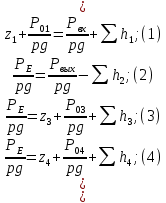
Рассмотрим первый трубопровод.
Вычисляем число Рейнольдса по расходу :
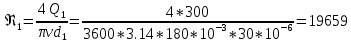
Определяем граничные числа Рейнольдса :

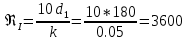 0
0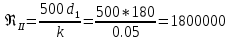
Так как Re <
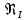 , определяем режим движения – турбулентный, зона гладкого трения и λ определяем по формуле Блазиуса :
, определяем режим движения – турбулентный, зона гладкого трения и λ определяем по формуле Блазиуса :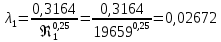
Тогда потери напора определим по формуле Вейсбаха :
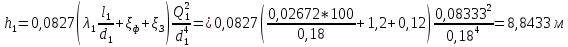
Определим
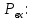
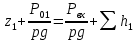
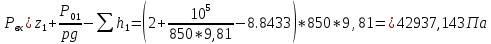
Рассматриваем трубопровод 2 :
Запишем уравнение Бернулли для второго трубопровода:
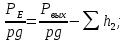
Найдем число Рейнольдса :
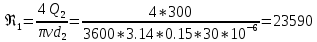
Определим граничные числа Рейнольдса:
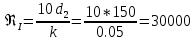 ;
;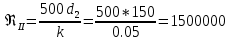 ;
; Так как
Так как 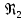 <
<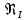 , определяем режим движения – турбулентный, зона гладкого трения и λ определяем по формуле Блазиуса :
, определяем режим движения – турбулентный, зона гладкого трения и λ определяем по формуле Блазиуса :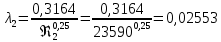
Тогда потери напора определим по формуле Вейсбаха :
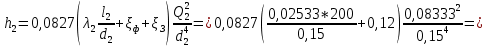 38,752 м
38,752 мГидростатический напор рассчитаем по формуле:
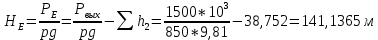
Уравнения (2), (3), (4) сведем в систему
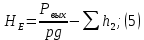
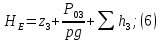
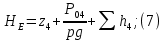
Так как
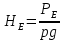 , найдем
, найдем 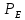 :
: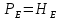
*
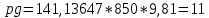 76866,448 Па.
76866,448 Па.Подставляем
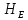 из уравнения (5) в уравнения (6) и (7), найдем потери напора
из уравнения (5) в уравнения (6) и (7), найдем потери напора 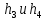 :
: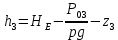 =141,13647-3-
=141,13647-3- 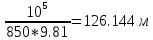
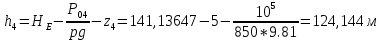
Рассматриваем трубопровод 3:
 Составляем уравнение Бернулли для трубопровода 3:
Составляем уравнение Бернулли для трубопровода 3: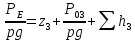
Задаемся режимом движения жидкости. Зона гидравлически гладких труб. Подставляем соответствующую формулу для
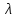 в формулу Блазиуса:
в формулу Блазиуса: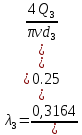
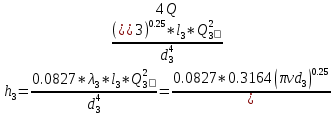
Откуда выразили
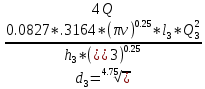 =0.0952
=0.0952Найдем число Рейнольдса :
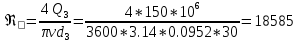
Вычисляем критическое значение числа Рейнольдса:
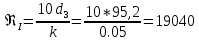
Найденное значение выходит в выбранную зону.
Выбираем диаметр от 0,08 до 0,14 м с шагом 0,01м .
Результаты расчетов сводим в соответствующие для каждого трубопровода таблицы.
Гидравлический расчет третьего трубопровода.
Таблица 1
| № | 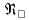 |  | 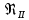 | Режим, формула | 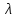 | d, м | h, м |
| 1 | 22118 | 16000 | 800000 | Смешанного трения, Альтшуля | 0,027129 | 0,08 | 297,214 |
| 2 | 19660 | 18000 | 900000 | Смешанного трения, Альтшуля | 0,027688 | 0,09 | 168,3353 |
| 3 | 17694 | 20000 | 1000000 | Гладкого трения, Блазиуса | 0,027433 | 0,10 | 98,485 |
| 4 | 16086 | 22000 | 1100000 | Гладкого трения, Блазиуса | 0,028095 | 0,11 | 62,626 |
| 5 | 14745 | 24000 | 1200000 | Гладкого трения, Блазиуса | 0,028713 | 0,12 | 41,425 |
| 6 | 13611 | 26000 | 1300000 | Гладкого трения, Блазиуса | 0,029293 | 0,13 | 28,323 |