ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 20
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
(наименование института полностью)
Кафедра /департамент /центр1 __________________________________________________
(наименование кафедры/департамента/центра полностью)
(код и наименование направления подготовки, специальности)
(направленность (профиль) / специализация)
Практическое задание №___
по учебному курсу «___________________________________»
(наименование учебного курса)
Вариант ____ (при наличии)
| Студент | | |
| | (И.О. Фамилия) | |
| Группа | | |
| | | |
| Преподаватель | | |
| | (И.О. Фамилия) | |
Тольятти 2021
Исходные данные
Горизонтальная поверхность массива грунта нагружена равномерно распределенной вертикальной нагрузкой интенсивностью р1 и р2. Размеры прямоугольных площадок в плане: l1 х b1 и l2 х b2.
Необходимо определить величины вертикальных напряжений σzp от совместного действия распределенных нагрузок на поверхности в грунтовой толще на вертикали, проходящей через точку M, на глубинах 1,0; 2,0; 3,0; 4,0; 5,0; 6,0 м. Расстояние между осями площадок нагружения – L = 3,0 м. По вычисленным напряжениям построить эпюру распределения σzp.
| № вар. | l1, м | b1, м | p1, кПа | l2, м | b2, м | p2, кПа |
| 4 | 2,6 | 2,1 | 340 | 5,0 | 2,4 | 380 |
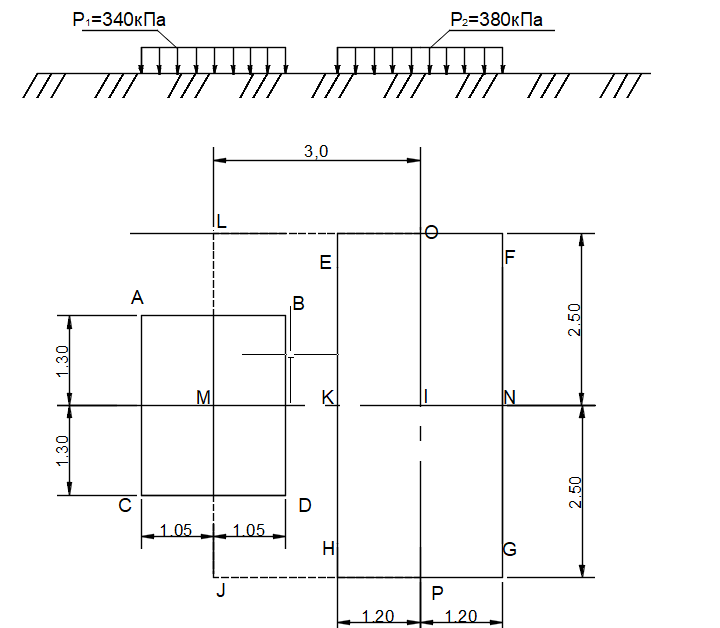
Рисунок 3.1 – Расчетная схема к заданию
Расчет напряжений и построение эпюры
Распределение по глубине вертикальных составляющих напряжений σzp в любой точке массива грунта от действия равномерно распределенной нагрузки в пределах или за пределами плит нагружения может быть определено по методу угловых точек.
Метод угловых точек применяется тогда, когда грузовая площадь может быть разбита на отдельные прямоугольники, в которых точка, соответствующая оси, является угловой.
Максимальное сжимающее напряжение для площадок под центром загружения прямоугольника определяется по формуле:
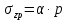, (3.1)где
α – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения
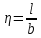(l – длинная сторона, b – меньшая сторона независимо от направления сторон, l > b) и относительной глубины 
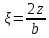(z – глубина, на которой определяется напряжение);p – интенсивность равномерно распределенной нагрузки.
Вертикальные напряжения по вертикали, проходящей через угловую точку загруженного прямоугольника, определяются по формуле:
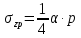, (3.2)где
α – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения
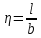(l – длинная сторона, b – короткая сторона независимо от направления сторон, l > b) и относительной глубины 
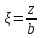(z – глубина, на которой определяется напряжение);p – интенсивность равномерно распределенной нагрузки.
Значения коэффициента α приведены в таблице В.1 приложения В.
В соответствии с этим плиты разбивают на прямоугольники таким образом, чтобы они имели общую угловую точку M.
Вводятся размеры соответствующих получившихся прямоугольников:
| Прямоуг. 1 (ABCD) | Прямоуг. 2 (MOFN) | Прямоуг. 3 (MNGP) | Прямоуг. 4 (MOEK) | Прямоуг. 5 (MKHP) |
| l1 = 2,6 м | l2 = 4,2 м | l3 = 4,2 м | l4 =2,5 м | l4 = 2,5 м |
| b1 2,1 м | b2 = 2,5 м | b3 = 2,5 м | b4 = 1,8 м | b4 = 1,8 м |
| p1 = 340 кПа | p2 = 380 кПа | P2 = 380 кПа | p2 = 380 кПа | p2 = 320 кПа |
Искомые напряжения в точке М от действия нагрузки по прямоугольникам 1, 2 и 3, взятые со знаком «+», прямоугольникам 4 и 5 со знаком «−», определяются по формуле:
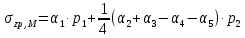(3.3)Вычисления рекомендуется вести в табличной форме.
Напряжения в точке № 1 (на глубине 1 м)
| № прямоуг. | zi, м | li, м | bi, м | pi, кПа | 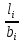 | 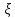 | αi | σzp |
| 1(+) | 1,0 | 2,6 | 2,1 | 340 | 1.24 | 0.95 | 0.752 | 255.68 |
| 2(+) | 4,2 | 2,5 | 380 | 1.68 | 0.80 | 0.973 | 92.44 | |
| 3(+) | 4,2 | 2,5 | 380 | 1.68 | 0.80 | 0.973 | 92.44 | |
| 4(−) | 2,5 | 1,8 | 380 | 1.39 | 1.11 | 0.912 | 86.64 | |
| 5(−) | 2,5 | 1,8 | 380 | 1.39 | 1.11 | 0.912 | 86.64 | |
 | ||||||||
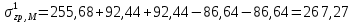Напряжения в точке № 2 (на глубине 2 м)
| № прямоуг. | zi, м | li, м | bi, м | pi, кПа |  |  | αi | σzp |
| 1(+) | 2,0 | 2,6 | 2,1 | 340 | 1.24 | 1.90 | 0.43 | 146.20 |
| 2(+) | 4,2 | 2,5 | 380 | 1.68 | 1.60 | 0.37 | 35.15 | |
| 3(+) | 4,2 | 2,5 | 380 | 1.68 | 1.60 | 0.97 | 92.15 | |
| 4(−) | 2,5 | 1,8 | 380 | 1.39 | 2.22 | 0.53 | 50.35 | |
| 5(−) | 2,5 | 1,8 | 380 | 1.39 | 2.22 | 0.53 | 50.35 | |
 | ||||||||
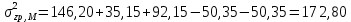Напряжения в точке № 3 (на глубине 3 м)
| № прямоуг. | zi, м | li, м | bi, м | pi, кПа | | | αi | σzp |
| 1(+) | 3,0 | 2,6 | 2,1 | 340 | 1.24 | 2.86 | 0.23 | 78.20 |
| 2(+) | 4,2 | 2,5 | 380 | 1.68 | 2.40 | 0.68 | 64.60 | |
| 3(+) | 4,2 | 2,5 | 380 | 1.68 | 2.40 | 0.68 | 64.60 | |
| 4(−) | 2,5 | 1,8 | 380 | 1.39 | 3.33 | 0.54 | 51.30 | |
| 5(−) | 2,5 | 1,8 | 380 | 1.39 | 3.33 | 0.54 | 51.30 | |
 | ||||||||
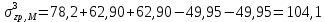Напряжения в точке № 4 (на глубине 4 м)
| № прямоуг. | zi, м | li, м | bi, м | pi, кПа | | | αi | σzp |
| 1(+) | 4,0 | 2,6 | 2,1 | 340 | 1.24 | 3.81 | 0,140 | 47,60 |
| 2(+) | 4,2 | 2,5 | 380 | 1.68 | 3.20 | 0,541 | 50,04 | |
| 3(+) | 4,2 | 2,5 | 380 | 1.68 | 3.20 | 0,541 | 50,04 | |
| 4(−) | 2,5 | 1,8 | 380 | 1.39 | 4.44 | 0,369 | 34,13 | |
| 5(−) | 2,5 | 1,8 | 380 | 1.39 | 4.44 | 0,369 | 34,13 | |
 | ||||||||
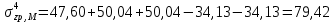Напряжения в точке № 5 (на глубине 5 м)
| № прямоуг. | zi, м | li, м | bi, м | pi, кПа | | | αi | σzp |
| 1(+) | 5,0 | 2,6 | 2,1 | 340 | 1.24 | 4.76 | 0,098 | 33,32 |
| 2(+) | 4,2 | 2,5 | 380 | 1.68 | 4.00 | 0,457 | 42,27 | |
| 3(+) | 4,2 | 2,5 | 380 | 1.68 | 4.00 | 0,457 | 42,27 | |
| 4(−) | 2,5 | 1,8 | 380 | 1.39 | 5.56 | 0,271 | 25,07 | |
| 5(−) | 2,5 | 1,8 | 380 | 1.39 | 5.56 | 0,271 | 25,07 | |
 | ||||||||
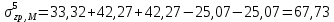