Файл: Эконометрика.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 61

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Рязанский государственный радиотехнический университет

имени В.Ф.Уткина»

Кафедра «Электронные вычислительные машины»

Отчёт о практическом занятии № 1

«Вероятностно- статистический аппарат эконометрики»

по дисциплине

«Эконометрика»

Выполнил:

Студент группы 1714

Субботин Д.А.

Проверил:

доц. каф. ЭВМ

Хруничев Р. В.

Рязань 2023

Цель работы: оценка свойств случайной величины (СВ) в генеральной совокупности по эмпирическим данным (выборке) путем построения эмпирического распределения, нахождения числовых характеристик СВ по выборке, нахождения точечных и интервальных оценок параметров распределения СВ в генеральной совокупности, проверки гипотезы о нормальном распределении СВ в генеральной совокупности.

Практическая часть

Вариант 8. СВ – время безотказной работы оборудования (тыс.

час.) по результатам 110 наблюдений.

14,64
12,7
14,9
11,33
8,84
12,87
13,78
13,51
11,75
11,2
11,91

12,72
10,26
13,48
12,06
13,64
12,93
11,07
14,21
11,6
11,55
17,22

14,74
12,68
12,72
16,81
14,29
11,47
8,29
12,79
12,29
11,27
8,8

13,22
11,81
10,52
13,27
9,7
12,73
14,68
12,21
12,87
15,89
13,65

13,52
14,15
11,71
12,78
8,39
11,26
12,26
10,91
14,23
12,5
13,7

11,47
13,72
11,85
13,64
15,53
12,77
17,04
9,07
11,83
10
12,62

15,59
10,52
13,31
12,95
12,46
9,49
14,49
14,25
14,01
16,13
13,66

11,6
13,06
12,15
13,48
10,84
14,08
11,08
12,1
13,32
17,71
12,91

17,39
15,55
13,55
15,54
13,67
11,28
14,84
9,22
11,94
13,7
11,7

13,2
12,87
13,56
15,78
11,43
12,75
12,95
12,5
14,02
12,54
16,26

По заданной выборке значений изучаемого признака генеральной совокупности (рисунок 1)

Рисунок 1 – Массив данных

Произведем ранжирование исходных данных в порядке возрастания (рисунок 2).

8,29
8,39
8,8
8,84
9,07
9,22
9,49
9,7
10
10,26
10,52

10,52
10,84
10,91
11,07
11,08
11,2
11,26
11,27
11,28
11,33
11,43

11,47
11,47
11,55
11,6
11,6
11,7
11,71
11,75
11,81
11,83
11,85

11,91
11,94
12,06
12,1
12,15
12,21
12,26
12,29
12,46
12,5
12,5

12,54
12,62
12,68
12,7
12,72
12,72
12,73
12,75
12,77
12,78
12,79

12,87
12,87
12,87
12,91
12,93
12,95
12,95
13,06
13,2
13,22
13,27

13,31
13,32
13,48
13,48
13,51
13,52
13,55
13,56
13,64
13,64
13,65

13,66
13,67
13,7
13,7
13,72
13,78
14,01
14,02
14,08
14,15
14,21

14,23
14,25
14,29
14,49
14,64
14,68
14,74
14,84
14,9
15,53
15,54

15,55
15,59
15,78
15,89
16,13
16,26
16,81
17,04
17,22
17,39
17,71


Рисунок 2 – Проранжированный массив данных во возрастанию

Составить интервальный вариационный ряд по ранжированному дискретному массиву.

Наименьшее значение выборки – 8,29, а наибольшее – 17,71; размах вариации R = 17,71-8,29=9,42. Число частичных интервалов можно оценить по правилу Стерджесса:

r= 1+ 3, 3lg n= 1+ 3, 3lg 110 = 7, 73 ≈ 8.

r=8, тогда размер каждого интервала составит:

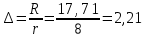
Находим частоту, соответствующую каждому интервалу, она будет равна сумме частот вариант, попавших в данный интервал, учитывая, что левый конец принадлежит интервалу. Также рассчитываем относительные частоты. Получим интервальный вариационный ряд частот (рисунок 3).

11,81
12,72
16,81
14,29
11,47
8,29
12,79
12,29
11,27
8,8

12,68
10,52
13,27
9,7
12,73
14,68
12,21
12,87
15,89
13,65

12,7
11,71
12,78
8,39
11,26
12,26
10,91
14,23
12,5
13,7

12,87
11,85
13,64
15,53
12,77
17,04
9,07
11,83
10
12,62

Рисунок 3 — Интервальный вариационный ряд частот

Проверяем, что сумма абсолютных частот равна объему выборки:

n= 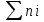= 110,

а сумма относительных частот – единице:

w= 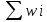=1.

Построим гистограмму относительных частот (рисунок 4).



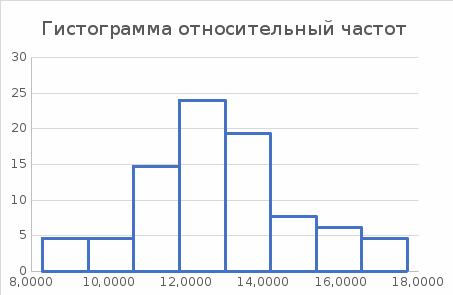
Рисунок 4 – Гистограмма

Чтобы построить кумуляту и эмпирическую функцию распределения, подсчитаем накопленные относительные частоты рисунок 5.


Частичный интервал Δ = 1,1775
Середины интервалов xi
Абсолютные частоты ni
Относительные частоты wi
Накопл. Отн. Частоты wiнак
xiwi
(xi)2wi
(xi- хср)3wi
(xi- хср)4wi

8,29-9,4675
8,879
6
0,054545455
0,054545455
0,4843
4,2999
-3,3890
13,4227

9,4675-10,645
10,056
6
0,054545455
0,109090909
0,5485
5,5161
-1,1759
3,2728

10,645-11,8225
11,234
19
0,172727273
0,281818182
1,9404
21,7977
-0,7151
1,1482

11,8225-13
12,411
31
0,281818182
0,563636364
3,4977
43,4110
-0,0221
0,0095

13-14,1775
13,589
25
0,227272727
0,790909091
3,0884
41,9668
0,0956
0,0716

14,1775-15,355
14,766
10
0,090909091
0,881818182
1,3424
19,8220
0,6503
1,2531

15,355-16,5325
15,944
8
0,072727273
0,954545455
1,1595
18,4875
2,1757
6,7540

16,5325-17,71
17,121
5
0,045454545
1
0,7782
13,3244
3,5683
15,2788

Сумма
110
1
-
12,8394
168,6255
1,1878
41,2107

Рисунок 5 – Расчет некоторых вспомогательных величин

Эмпирическая функция распределения (по накопленным частотам рисунок 5):



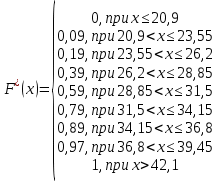
График эмпирической функции распределения F*(x) – рисунок 6. Более наглядно эмпирическая функция распределения описывается кумулятой (рисунок 7), которая дает представление о виде функции распределения СВ в генеральной совокупности.



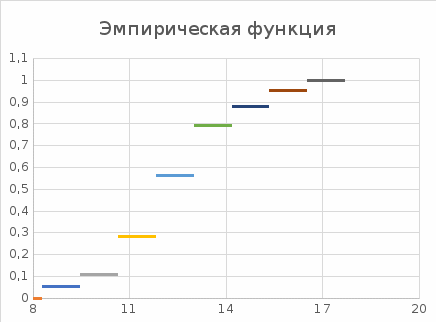
Рисунок 6 – График эмпирической функции



Рисунок 7 – Кумулята

Вычислим методом произведения точечные оценки параметров распределения, используя рисунок 5.

Выборочное среднее:



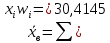
Выборочная дисперсия:

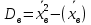2 = 947,466325-( 30,4135)2 =22,4853428

Исправленная выборочная дисперсия:



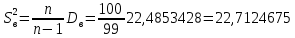
Выборочное среднее квадратическое отклонение:



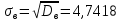
Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Моду для интервального распределения определяем по формуле:



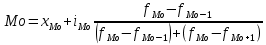
где хМо– нижняя граница модального интервала, iМо– величина модального интервала, fМо,fМо-1,fМо+1– соответственно частоты модального, предмодального (предыдущего) и послемодального (следующего за модальным) интервалов.

Модальный интервал (интервал с наибольшей честотностью) – от 26,2 до 28,85. Тогда

Смотрите также файлы