Добавлен: 09.11.2023
Просмотров: 62
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
мода
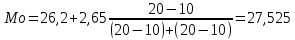
Медиана (Ме) – значение признака, приходящееся на середину ранжированной совокупности. Определяется в интервальном вариационном ряду по формуле:
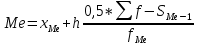
где xMe начальное значение интервала, содержащего медиану; h величина медианного интервала; ∑f сумма частот ряда; SMe-1 сумма накопленных частот, предшествующих медианному интервалу; fMe частота медианного интервала.
Медианным является тот интервал, накопленная частота которого равна полусумме или превышает полусумму всех частот ряда (fMe = =0,5f). У нас это интервал от 26,2 до 28,85. Тогда медиана:
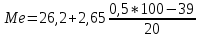= 27,6575
Коэффициент асимметрии:
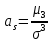
где в числителе – центральный момент третьего порядка (рисунок 5).
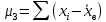3wi= - 59,96951656
Тогда коэффициент асимметрии:
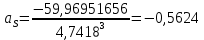
Эксцесс - величина, определяемая формулой:
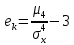
где в числителе – центральный момент четвертого порядка (таблица 2):
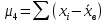4wi=
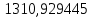
Тогда эксцесс:
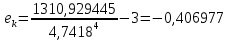
Доверительный интервал для математического ожидания нормально распределенного признака с надежностью γ определяется из условия:
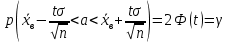
где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2Ф(t) = γ.
В условиях примера имеем: Ф(t)= γ/2 = 0,95/2 = 0,475. По таблице для функции Лапласа находим аргумент: t= 1.96.
Имеем:
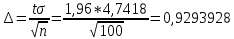
Получаем 95%-ный доверительный интервал:
(хср-Δ; хср+Δ) = (30,4135–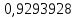
; 30,4135+ 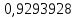) = (29,4841072
; 31,3428928).
По итогам предыдущих пунктов целесообразно выдвинуть гипотезу H0 – «данный признак Храспределен нормально».
Для того, чтобы при заданном уровне значимости проверить гипотезу о нормальном распределении наблюдаемого признака, надо:
а) вычислить теоретические частоты;
б) вычислить наблюдаемое значение критерия χ2 Пирсона по формуле
где ni*- эмпирические частоты, ni- теоретические частоты;
в) по таблице критических точек распределения χ2, по заданному уровню значимости α=0,05 и числу степеней свободы k=s-1-r , где s – число частичных интервалов, r – число параметров предполагаемого распределения, найти критическую точку χ2кр (α; k);
г) если χ2набл < χ2кр, то гипотеза о нормальном распределении наблюдаемого признака принимается; если χ2набл > χ2кр, то гипотеза отвергается.
Для нахождения теоретических частот составим расчетную таблицу. Удобнее всего это сделать в Excel, используя функцию НОРМРАСП (рисунок 8).
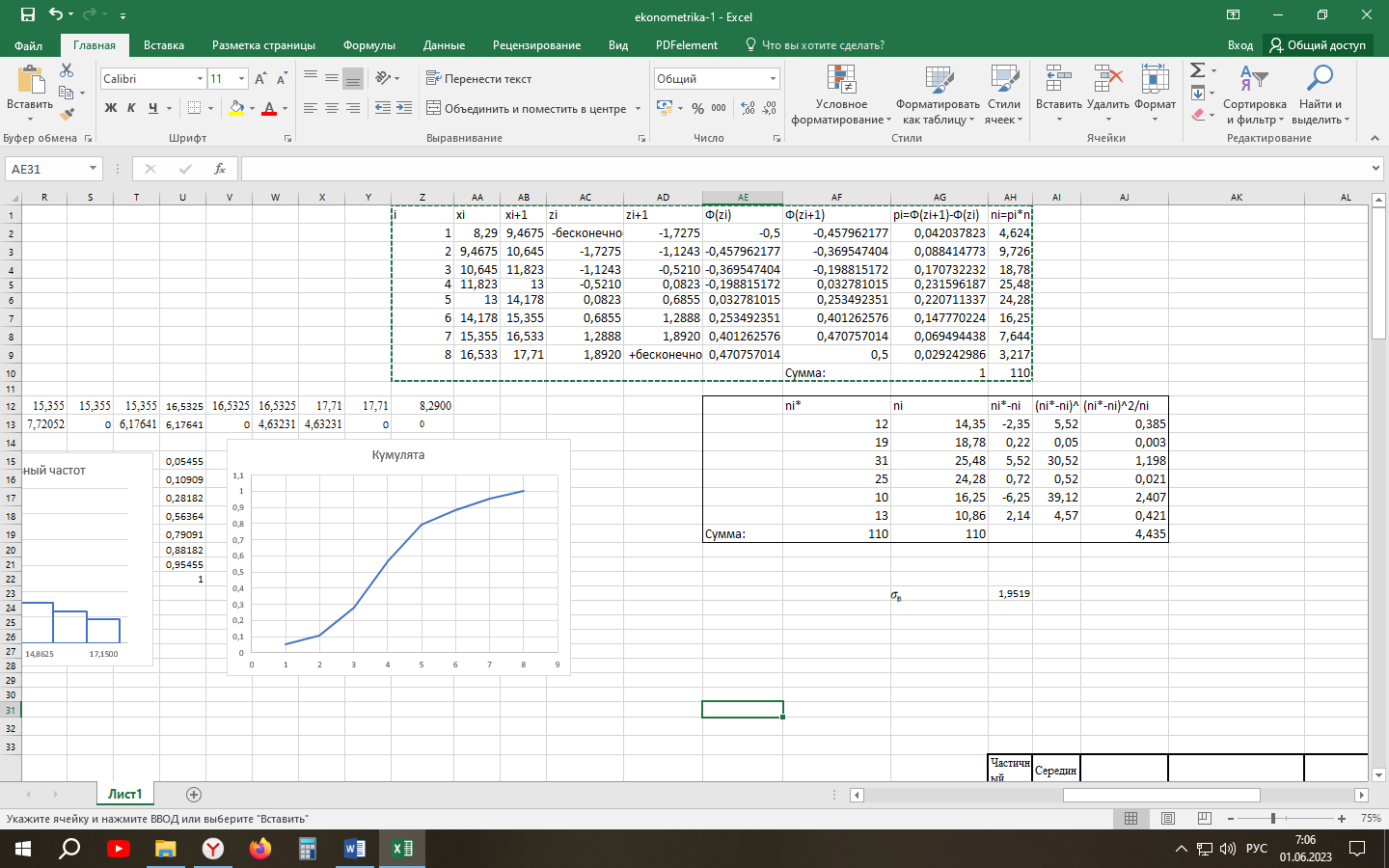
Рисунок 8 – Таблица для расчета теоретических частот
Для нахождения наблюдаемого значения критерия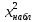
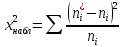
Рисунок 9 – Расчет наблюдаемого значения критерия хи-квадрат (малые частоты <5 объединены).
Так как уровень значимости α=0,05, число частичных интервалов (после объединения) равно s=7, число параметров нормального распределения r=2, то число степеней свободы распределения χ2 равно k=7-1-2=4, тогда по таблице критических точек находим критическую точку распределения χ2, она равна χ2крит = 7,8. Поскольку χ2набл<χ2крит (9,165<9,5), то гипотеза Н0 о нормальном распределении признака Х принимается.
Заключение
В ходе работы были оценены
свойства случайной величины (СВ) в генеральной совокупности по эмпирическим данным (выборке) путем построения эмпирического распределения, нахождения числовых характеристик СВ по выборке, нахождения точечных и интервальных оценок параметров распределения СВ в генеральной совокупности, проверки гипотезы о нормальном распределении СВ в генеральной совокупности.5>
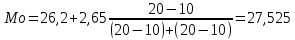
Медиана (Ме) – значение признака, приходящееся на середину ранжированной совокупности. Определяется в интервальном вариационном ряду по формуле:
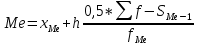
где xMe начальное значение интервала, содержащего медиану; h величина медианного интервала; ∑f сумма частот ряда; SMe-1 сумма накопленных частот, предшествующих медианному интервалу; fMe частота медианного интервала.
Медианным является тот интервал, накопленная частота которого равна полусумме или превышает полусумму всех частот ряда (fMe = =0,5f). У нас это интервал от 26,2 до 28,85. Тогда медиана:
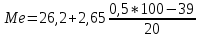= 27,6575Коэффициент асимметрии:
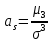
где в числителе – центральный момент третьего порядка (рисунок 5).
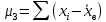3wi= - 59,96951656Тогда коэффициент асимметрии:
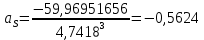
Эксцесс - величина, определяемая формулой:
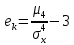
где в числителе – центральный момент четвертого порядка (таблица 2):
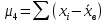4wi=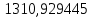 Тогда эксцесс:
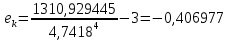
Доверительный интервал для математического ожидания нормально распределенного признака с надежностью γ определяется из условия:
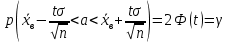
где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2Ф(t) = γ.
В условиях примера имеем: Ф(t)= γ/2 = 0,95/2 = 0,475. По таблице для функции Лапласа находим аргумент: t= 1.96.
Имеем:
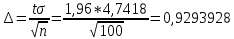
Получаем 95%-ный доверительный интервал:
(хср-Δ; хср+Δ) = (30,4135–
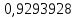; 30,4135+ 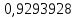) = (29,4841072; 31,3428928).
По итогам предыдущих пунктов целесообразно выдвинуть гипотезу H0 – «данный признак Храспределен нормально».
Для того, чтобы при заданном уровне значимости проверить гипотезу о нормальном распределении наблюдаемого признака, надо:
а) вычислить теоретические частоты;
б) вычислить наблюдаемое значение критерия χ2 Пирсона по формуле
где ni*- эмпирические частоты, ni- теоретические частоты;
в) по таблице критических точек распределения χ2, по заданному уровню значимости α=0,05 и числу степеней свободы k=s-1-r , где s – число частичных интервалов, r – число параметров предполагаемого распределения, найти критическую точку χ2кр (α; k);
г) если χ2набл < χ2кр, то гипотеза о нормальном распределении наблюдаемого признака принимается; если χ2набл > χ2кр, то гипотеза отвергается.
Для нахождения теоретических частот составим расчетную таблицу. Удобнее всего это сделать в Excel, используя функцию НОРМРАСП (рисунок 8).
Рисунок 8 – Таблица для расчета теоретических частот
Для нахождения наблюдаемого значения критерия
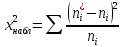
| | ni* | ni | ni*-ni | (ni*-ni)^2 | (ni*-ni)^2/ni |
| | 12 | 14,35 | -2,35 | 5,52 | 0,385 |
| | 19 | 18,78 | 0,22 | 0,05 | 0,003 |
| | 31 | 25,48 | 5,52 | 30,52 | 1,198 |
| | 25 | 24,28 | 0,72 | 0,52 | 0,021 |
| | 10 | 16,25 | -6,25 | 39,12 | 2,407 |
| | 13 | 10,86 | 2,14 | 4,57 | 0,421 |
| Сумма: | 110 | 110 | | | 4,435 |
Рисунок 9 – Расчет наблюдаемого значения критерия хи-квадрат (малые частоты <5 объединены).
Так как уровень значимости α=0,05, число частичных интервалов (после объединения) равно s=7, число параметров нормального распределения r=2, то число степеней свободы распределения χ2 равно k=7-1-2=4, тогда по таблице критических точек находим критическую точку распределения χ2, она равна χ2крит = 7,8. Поскольку χ2набл<χ2крит (9,165<9,5), то гипотеза Н0 о нормальном распределении признака Х принимается.
Заключение
В ходе работы были оценены
свойства случайной величины (СВ) в генеральной совокупности по эмпирическим данным (выборке) путем построения эмпирического распределения, нахождения числовых характеристик СВ по выборке, нахождения точечных и интервальных оценок параметров распределения СВ в генеральной совокупности, проверки гипотезы о нормальном распределении СВ в генеральной совокупности.5>