Файл: Задача 137 Заряд равномерно распределен по всему объему однородного сферического диэлектрика ( 3 ) радиусом r 5,0 см.doc
Добавлен: 09.11.2023
Просмотров: 377
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача № 137
Заряд
Построить графики функций
-
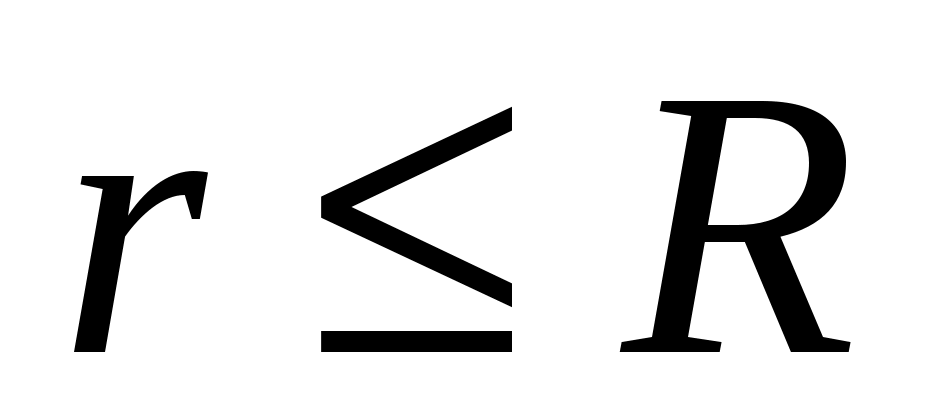 : 2)
: 2) 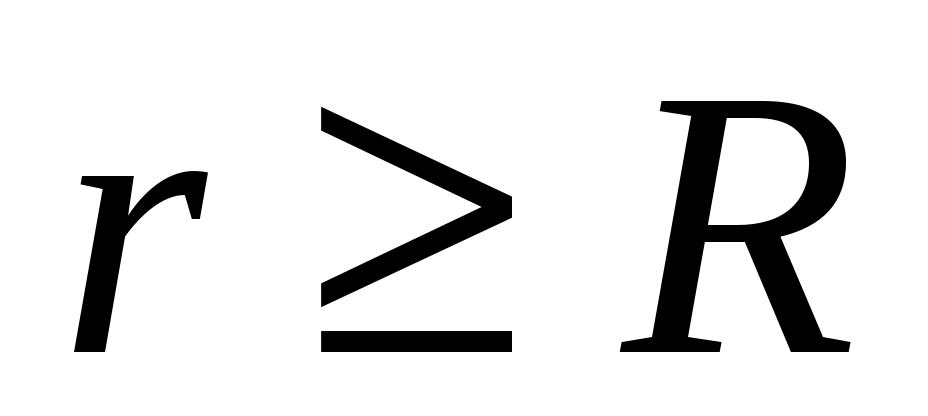
Вычислить разность потенциалов
Дано:
-
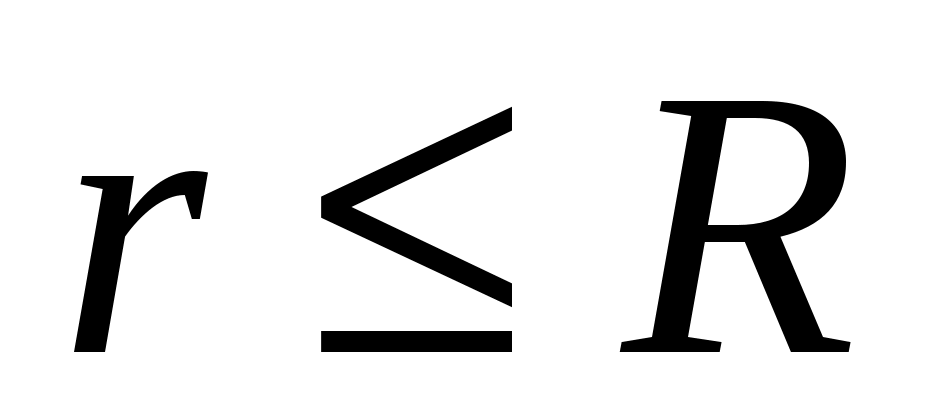 : 2)
: 2) 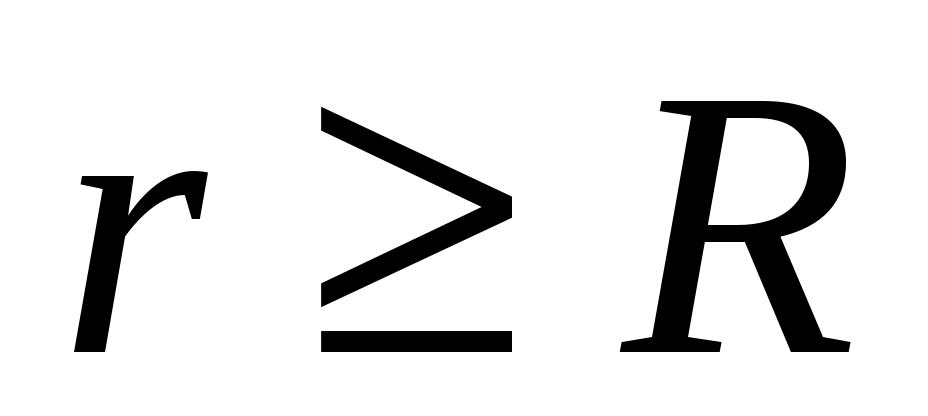
Найти: 1)
Рисунок:
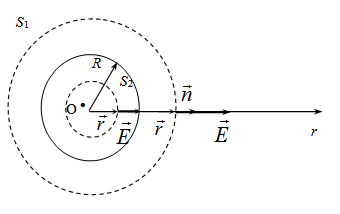
Физический смысл имеет только разность потенциалов, и если в задаче требуется найти значение потенциала в некоторой точке, то предполагается, что его значение в другой точке известно. Такой общепринятой во многих случаях является точка, бесконечно удаленная от заряженного объекта (r), где потенциал полагается равным нулю. Значение же его в центре шара зависит от характера распределения заряда. Поскольку этот характер различен внутри и вне шара, необходимо решать последовательно внешнюю задачу (чтобы найти потенциал на поверхности шара), а затем – внутреннюю. Поле однородно заряженного шара центрально-симметрично
, т.е. вектор напряженности выражается через радиус - вектор
В таком поле потенциал связан с напряженностью соотношением:
Для этого воспользуемся теоремой Остроградского – Гаусса:
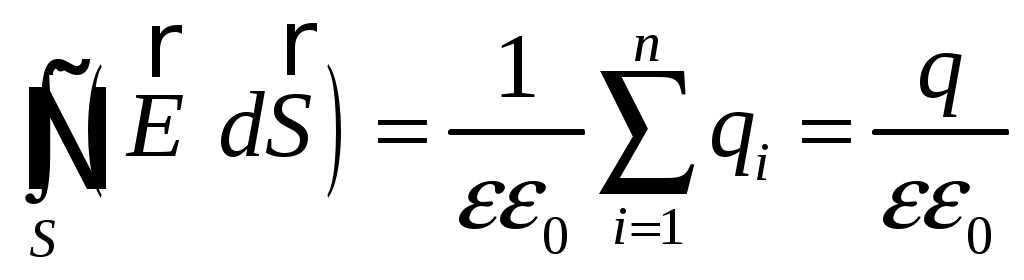 и запишем выражение для потока вектора
и запишем выражение для потока вектора 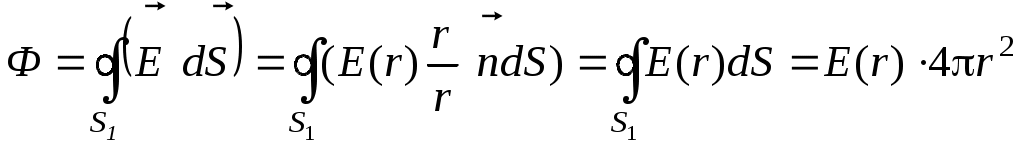 (1)
(1)Здесь учтено, что скалярное произведение вектора
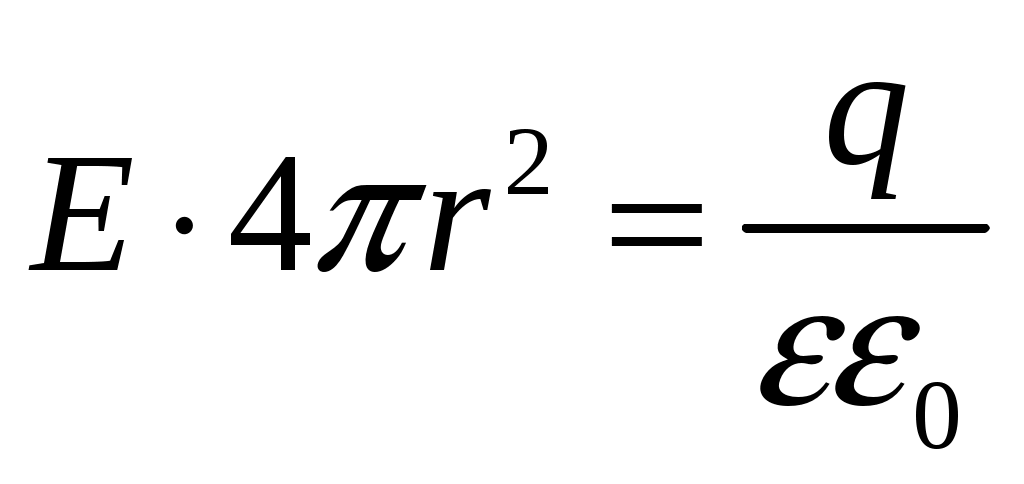 (2)
(2)Итак, для r > R получаем:
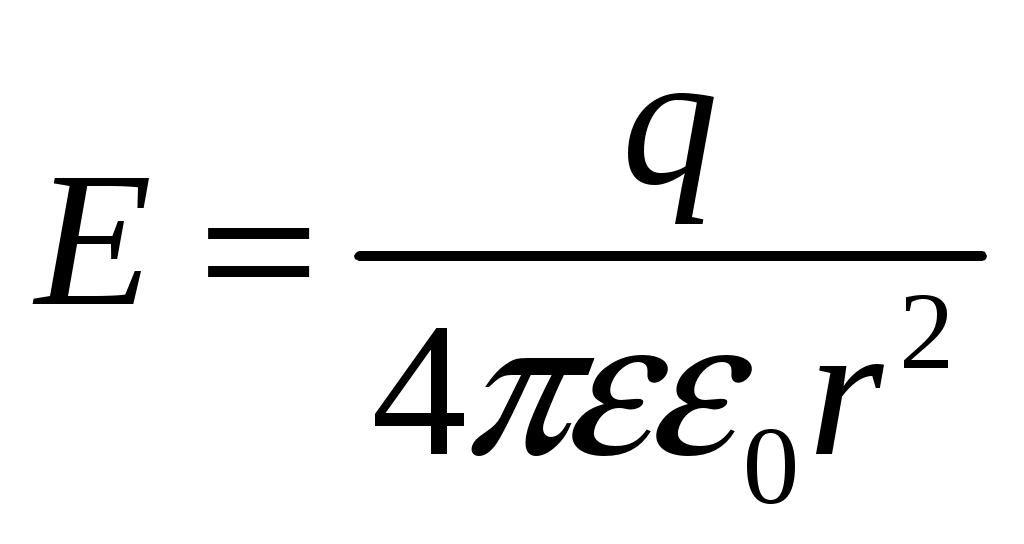 , (3)
, (3)Откуда:
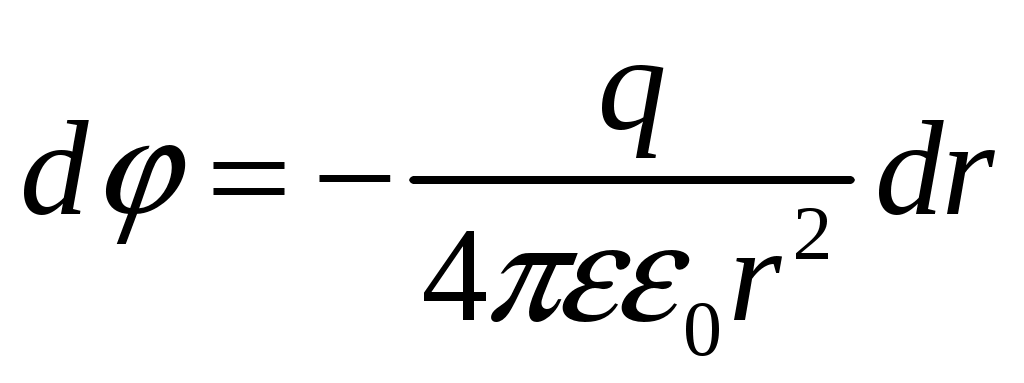 (4)
(4)В результате интегрирования в пределах от точки с произвольным r до точки r, где = 0, получаем:
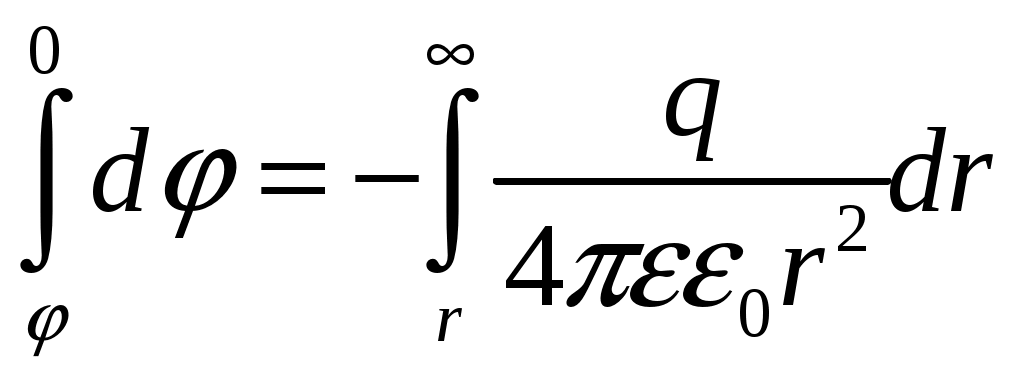 (5)
(5)или:
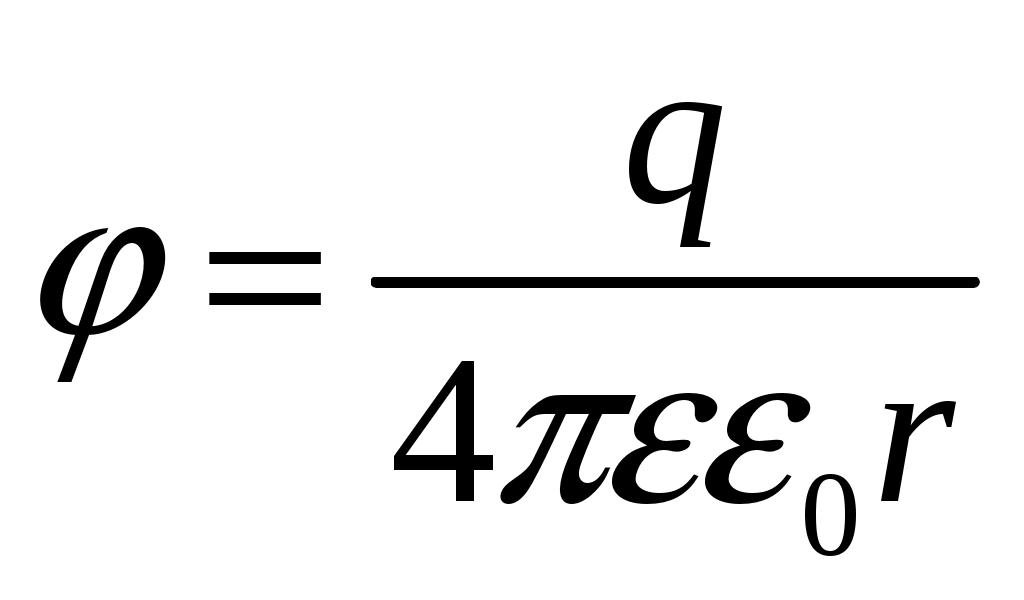 (6)
(6)В частности, при rR получаем:
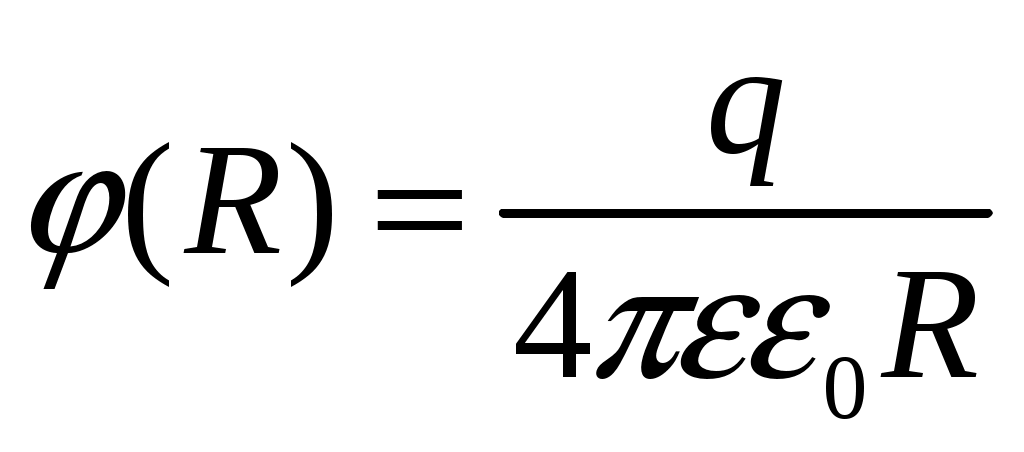 (7)
(7)Теперь при решении внутренней задачи точка на поверхности шара (r = R) будет выступать как точка с известным значением потенциала, задаваемым формулой (7).
Опять рассмотрим сферическую поверхность S2, построенную теперь уже внутри шара, т.е. r<R. Поток вектора напряженности через нее по-прежнему выражается формулой (1). Но охваченный ею заряд
q/ меньше заряда шара q. При постоянной объемной плотности заряда :
q/ =(4/3)r3, q = (4/3)R3. (8)
Исключая , получим:
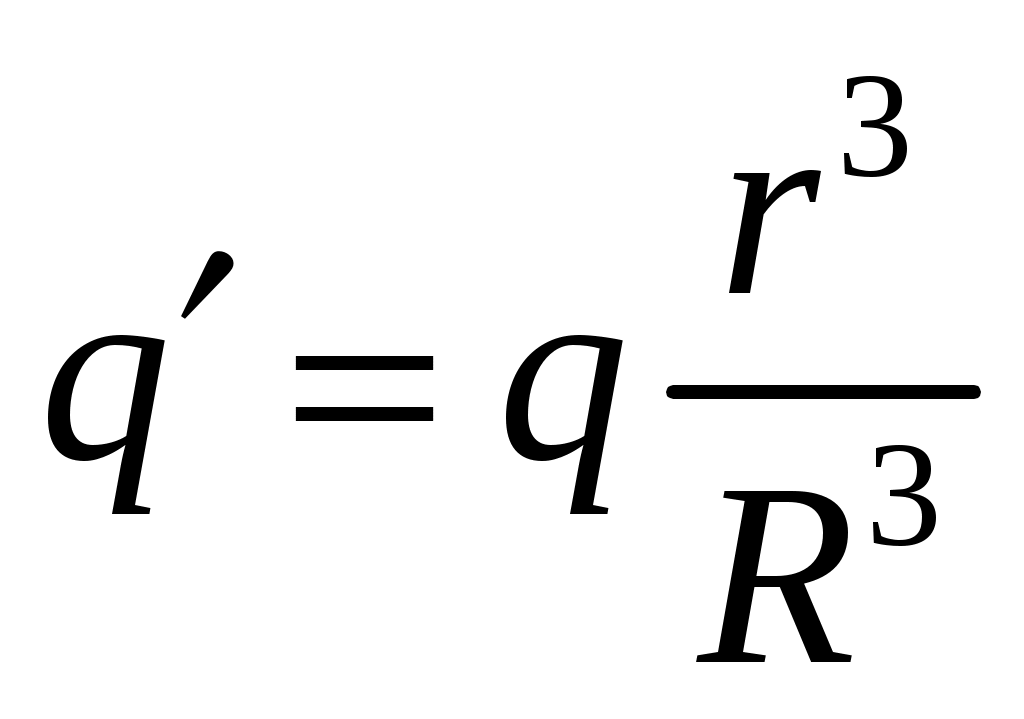 (9)
(9)Тогда согласно формуле
 получаем:
получаем: 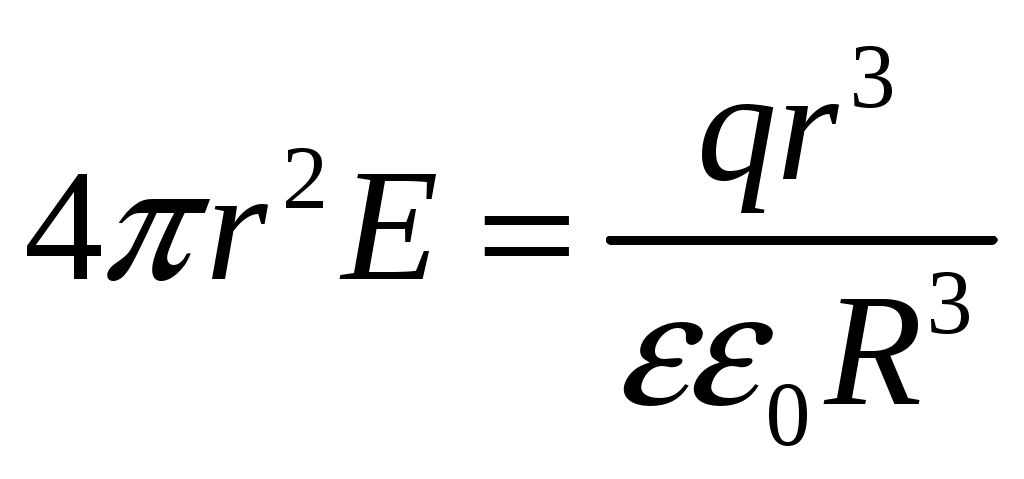 (10)
(10)Итак, для r < R получаем:
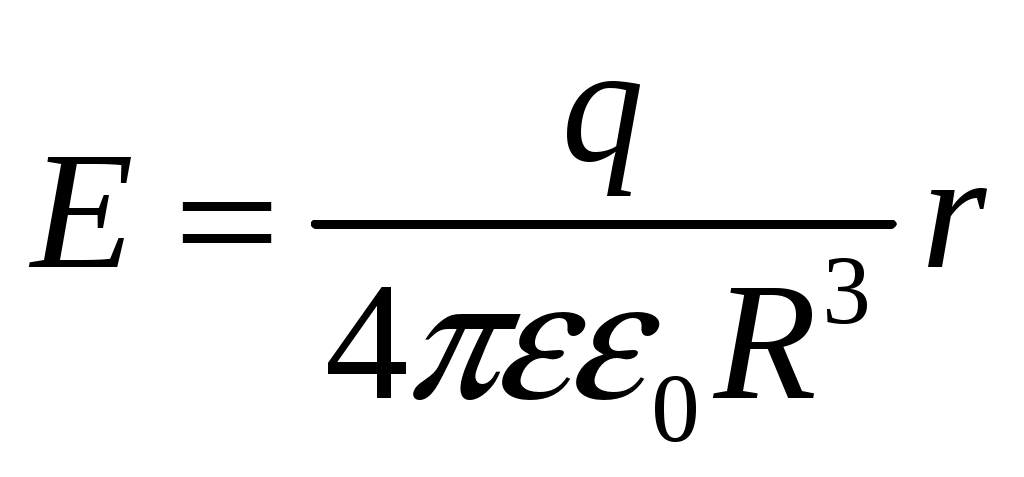 (11)
(11)Заметим, что при r =R формулы (3) и (11) дают одинаковое значение:
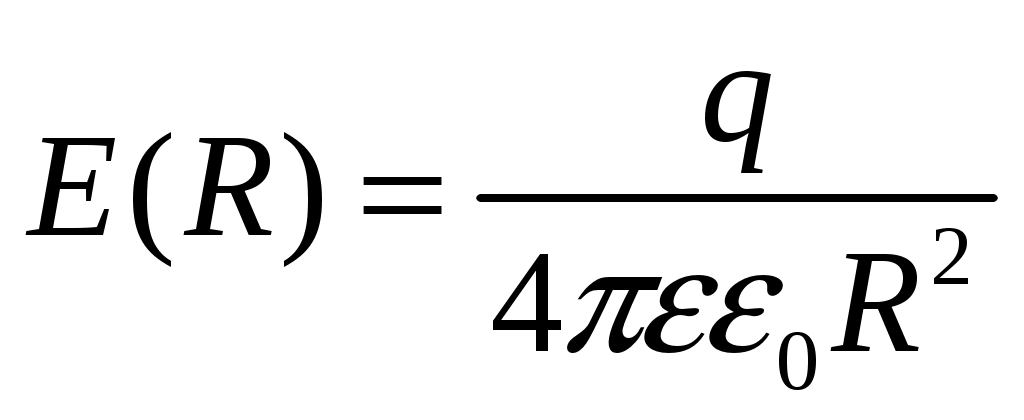 (12)
(12)Тогда потенциал равен:
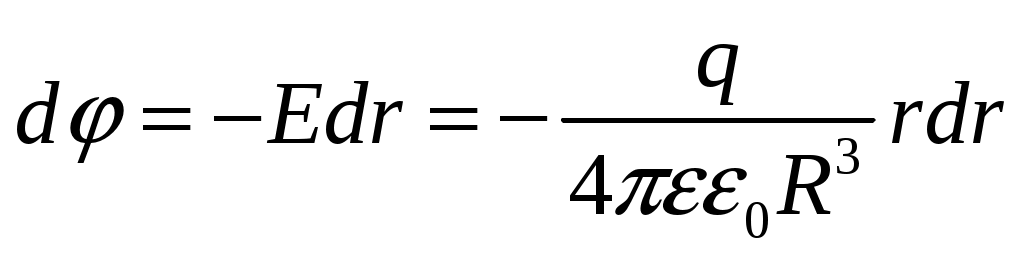 (13)
(13)Интегрируя в пределах от произвольного r до R, получаем:
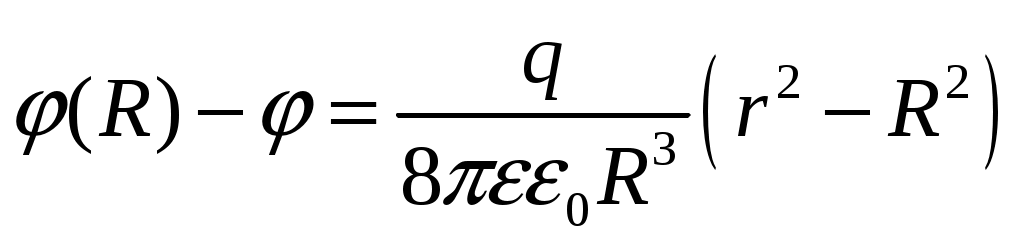 (14)
(14)Подставляя (R) из (7), после преобразований получаем зависимость потенциала от координаты внутри шара:
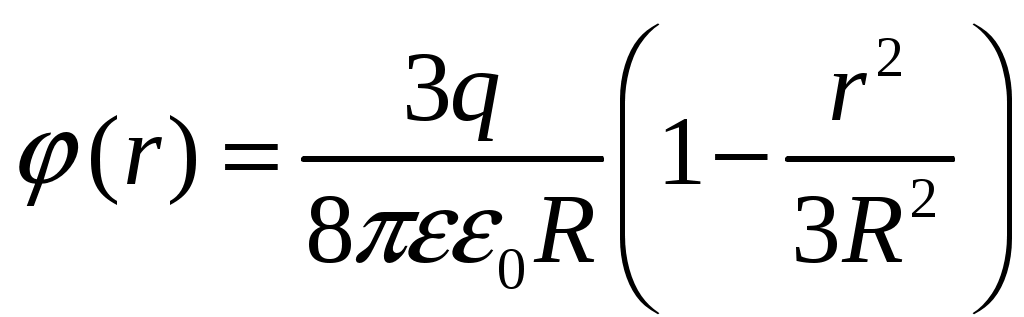 (15)
(15)В частности, при r = 0, т.е. в центре шара по формуле (15):
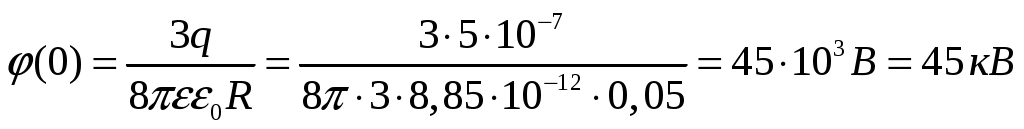
где
При
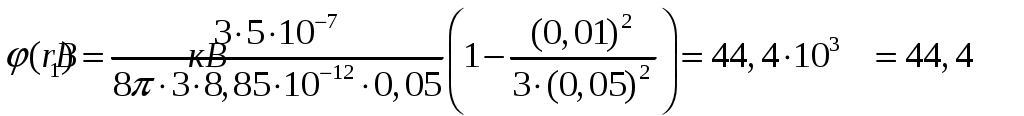
При
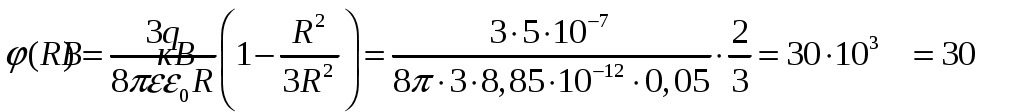
Для точек вне шара
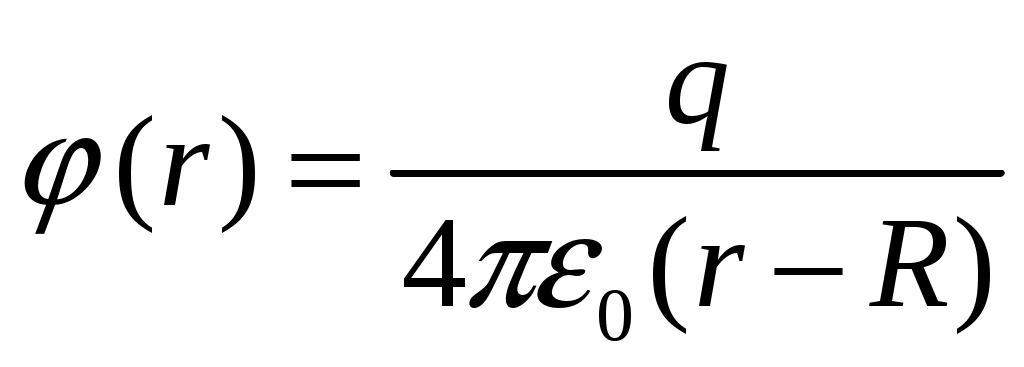 (16)
(16)Найдем потенциал для точки
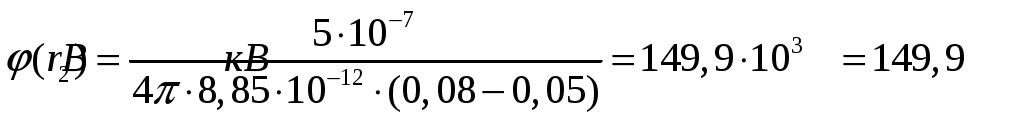
Найдем разность потенциалов
Построим графики функций
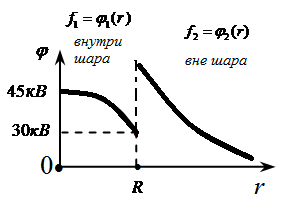
Ответ: