Алгоритм поиска вещественных корней квадратного уравнения:

1. 
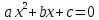
   Задать значение коэффициентов a,b,c.
   
2. 
   Вычислить дискриминант .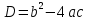
   
3. 
   Проверить условие существования вещественных корней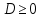 , то перейти к следующему шагу. Если 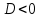- условие не выполнено, корней нет.
   
4. 
   Проверить условие существования корней и вычислить корни уравнения. .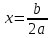
   
5. 
   Вычислим корни уравнения \ .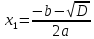
   
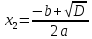6. 
   Закончить вычисление.
   

1. 
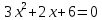
   A= 3, b=2, c=6 .
   
2. 
   
   
3. 
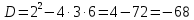
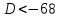   - корней нет
   

Блок схема

	Начало и конец алгоритма.
	Блок ввода и вывода информации.
	Блок обработки, внутри блока записывают формулы, обозначения операций и функций.
	Блок выбора. Внутри блока записываются условия выбора следующего действия алгоритма.
	Блок заголовка цикла с параметром.
	Соединительный блок.

Алгоритм упражнения

Упражнения.

1. 
   На примере умножения числа 357 на 4 проиллюстрируйте теоретические основы алгоритма умножения многозначного числа на однозначное.
   

---

Решение: 1) Разложим число 357 на разрядные слагаемые:

357 = 300 + 50 + 7

2) Чтобы умножить сумму чисел на число, надо каждое слагаемое умножить на это число и сложить полученные результаты (распределительное свойство умножения):

= (300 + 50 + 7) · 4 = 300 · 4 + 50 · 4 + 7 · 4 = 1200 + 200 + 28 = 1428

Ответ: 1428.

2. 
   На примере умножения 452 на 186 проиллюстрируйте теоретические основы алгоритма умножения многозначного числа на многозначное.
   

Решение: Смысл умножения сохраняется и для многознач­ных чисел, но меняется техника вычислений. Произведение много­значных чисел, как правило, находят, выполняя умножение столби­ком, по определенному алгоритму. Выясним, каким образом возника­ет этот алгоритм, какие теоретические факты лежат в его основе.

3. 
   Объясните, почему нижеприведенные задачи решаются при по­мощи умножения чисел и решите их.
   

а) Земля при обращении вокруг Солнца за сутки проходит пример­но 2 505 624 км. Какой путь проходит Земля за 365 дней?

Решение:  год = 365 дней (если год не високосный)
2505624 * 365 = 914552760 (км) - за 1 год.
Ответ: 914552760

б) В школу привезли 56 пачек книг, по 24 книги в каждой пачке. Сколько всего книг привезли в школу?

Решение: Объяснение: если 56 пачек и в каждой по 24 книги то: 56×24=1344

Ответ:1344

4. Решение задачи запишите в виде числового выражения, а затем найдите его значение:

а) На элеватор отвезли 472 т овса, ржи на 236 т больше, чем овса, а пшеницы в 4 раза больше, чем овса и ржи вместе. Сколько тонн пшеницы отвезли на элеватор?

Решение: Овса - 472 ц

Ржи - ? ц, на 236 ц > , (чем овса (стрелка от ржи к овсу))

Пшеницы - ? ц, в 4 раза > , (чем овса и ржи вместе( рисуешь фигургую скобку от овса до ржи, а затем рисуешь стрелку от пшеницы до фигурной скобки))

Пшеницы - ? ц

1) 472+236=708 (ц) - ржи.

2) 472+708=1 180 (ц) - овса и ржи вместе.

3) 1 180·4=4 720 (ц) - пшеницы.

Ответ: на элеватор отвезли 4 720 центнеров пшеницы.

б) Столяр делает в день 18 рам, а его помощник на 4 рамы меньше. Сколько рам они сделают за 24 дня, если каждый день будут работать вместе?

Решение: Нам известно, что первый столяр делает 18 рам. Найдём для начала сколько рам делает помощник столяра. Дальше количество рам вместе за один день, а потом умножим эту сумму на количество дней. 

Составим числовое выражение для решения задачи.

(18 + (18 - 4) ) *24

Решим наше числовое выражение.

(18 + 14)*24= 32*24=768

---

Ответ: 768 рам сделают за 24 дня столяр и его помощник, если будут работать вместе.

 

5. Как могут рассуждать учащиеся, выполняя следующее задание:
«Ширина земельного участка прямоугольной формы равна 24 м. Это в 6 раз меньше его длины. Объясни, что обозначают выражения, записанные по условию задачи, и вычисли их значения: 24 × 6; 24× (24× 6); (24 + 24 × 6) × 6; 24 × 2; 24× 2 + 24 × 6 × 2».

6. Выполните умножение чисел, используя запись столбиком, и объясняя каждый шаг алгоритма:

а) 984 × 27; в) 7040 × 234;

6) 8276 × 73; г) 4569 × 357.

7. Используя свойства умножения, найдите наиболее рациональ­ным способом значение выражения:

а) 8× 13 × 4125× 25; г) 124× 4 + 116× 4;

б) 24× (27 × 125); д) (3750 - 125) × 8;

в) (88 + 48) × 125; е) 1779× 1243 – 779× 1243.

8. Зная, что 650-34 = 22100, найдите произведение чисел, не выпол­няя умножения столбиком:

а) 650 • 36; б) 650 • 32; в) 649•34.

9. Найдите и обоснуйте приемы умножения 24 на 35 и, пользуясь ими, умножьте на 35 числа: 12, 18, 24, 32, 48, 64.

10. Вычислите рациональным способом значение выражения:

а) (420 -394) • 405 – 25 • 405;

б) 105 • 209 + (964 - 859) • 209 • 400.

11. Найдите значения выражений 13•11, 27•11, 35•11, 43•11, 54•11.
Верно ли: чтобы найти результат умножения двузначного числа на 11 в случае, когда сумма цифр двузначного числа меньше 10, достаточно между цифрами данного числа написать число, равное сумме его цифр?

12. Найдите значение выражений 29 • 11, 37 • 11, 47 • 11, 85 • 11, 97 • 11.
Верно ли: чтобы найти результат умножения двузначного числа на 11 в случае, когда сумма цифр двузначного числа больше или равна 10, достаточно между цифрой десятков, увеличенной на 1, и цифрой еди­ниц написать число, равное разности между суммой его цифр и чис­лом 10?

13. На множестве выражений, приведенных ниже, задано отноше­ние «содержать в произведении цифру 0». Определяет ли оно разбие­ние этого множества на классы? Если да, то выполните его, не вычис­ляя произведений.

2602•3 1803•6 17009•4

2602•7 1803•2 17019•4

26002•8 18003•7 17019•7.

 

---

Смотрите также файлы

• Парикмахерское искусство.docx

• Контрольная работа выполняется в формате Microsoft Word. Работа в каждой из 4 тем состоит из одного практического задания и ситуационной задачи..docx

• Задание на курсовую работу введение.docx

• Решение далее.pdf

• Шумихина яна александровна.docx