Добавлен: 09.11.2023
Просмотров: 89
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рассмотрим простейшую форму ЦПТ.
Если
независимые случайные величины, имеющие одно и то же распределение (М(Х1) ==
для всех i), то при увеличении n закон распределения суммы 
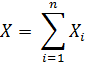
неограниченно приближается к нормальному закону распределения.
Сформулированная теорема используется в двух основных случаях: для суммы независимых случайных величин и для их среднего арифметического. [7]
Сумма независимых случайных величин. [1]
Имеем
, Найдем параметры распределения случайной величины X
:
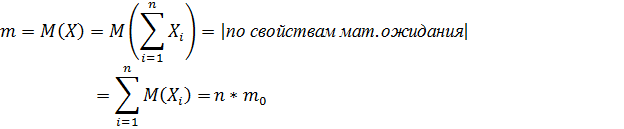
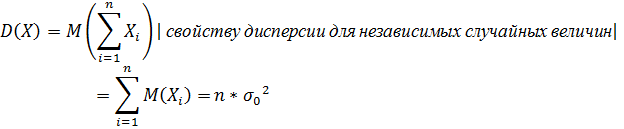
Таким образом, для случайной величины Х-суммы случайных величин
-параметры нормального закона следующие:
Среднее арифметическое независимых случайных величин.
Имеем
. Здесь 
, где случайная величина Х распределена нормально, и ее параметры найдены. В этом случае 
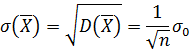
Таким образом, для случайной величины
- среднего арифметического случайных величин Х-получаем:
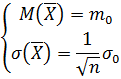
Т.е. математическое ожидание то же, что и у отдельных слагаемых Х
i, а среднее квадратическое отклонение - в
раз меньше. На этом свойстве основана обработка результатов физических измерений, когда усредняются результаты n независимых экспериментов: с ростом числа измерений величина 
становится все менее случайной, так как 
при 
. [1]2.Практическая часть
Задача №1
Заблудившись в лесу, мальчик вышел на поляну, откуда вело 5 дорог. Известно, что для различных дорог вероятности выхода из леса за час соответственно равны 0,6; 0,3; 0,2; 0,1; 0,1. Определить вероятность того, что заблудившийся мальчик пошел по первой дороге, если известно, что он вышел из леса через час.
Решение:
А-мальчик вышел из леса через час.
=мальчик пошел по первой дороге;
=мальчик пошел по второй дороге;
= мальчик пошел по третьей дороге;
= мальчик пошел по четвертой дороге;
= мальчик пошел по пятой дороге.Р (
)= Р ( )= Р ( )= Р ( )= Р ( )=0,2
А) =0,6
(А) =0,2
(А) =0,3
(А) =0,1
(А) =0,1Р(А)= Р(
)*
+
+
Р(А)= 0,2*0,6+0,2*0,3+0,2*0,2+0,2*0,1+0,2*0,1=0,26
=
=
=0,46Ответ: вероятность того, что заблудившийся мальчик пошел по первой дороге равна 0,46.
Задача №2
Рабочий обслуживает 4 независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,7, для второго-0,75, для третьего-0,8, для четвертого-0,9. Найдите закон распределения случайной величины х, равной числу станков, которые не потребуют внимания рабочего.
Решение:
х-станок не потребует внимания.
=0 (ни один станок не потребует внимания рабочего);
=1 (1 станок не потребует внимания рабочего);
=2 (2 станка не потребуют внимания рабочего);
=3 (3 станка не потребуют внимания рабочего);
=4 (4 станка не потребуют внимания рабочего).Р(х=0) =0,3*0,25*0,2*0,1=0,0015
Р(х=1) = =0,7*0,25*0,2*0,1+0,3*0,75*0,2*0,1+0,3*0,25*0,8*0,1+0,3*0,25*0,2*0,9=
=0,0275
Р(х=2) = =0,7*0,75*0,2*0,1+0,7*0,25*0,8*0,1+0,7*0,25*0,2*0,9+0,3*0,75*0,8*0,1+0,3*
*0,75*0,2*0,9+0,3*0,25*0,8*0,9=0,1685
Р(х=3) =0,7*0,75*0,8*0,1+0,7*0,75*0,2*0,9+0,7*0,25*0,8*0,9+0,3*0,75*0,8*0,9=
=0,4245
Р(х=4) =0,7*0,75*0,8*0,9=0,378
Ответ:
| х | 0 | 1 | 2 | 3 | 4 |
| Р | 0,0015 | 0,0275 | 0,1685 | 0,4245 | 0,378 |
Задача №3
Дана плотность вероятность f(x) непрерывной случайной величины Х. Требуется:
. Найти параметр
. Найти числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое, ассиметрию и эксцесс.
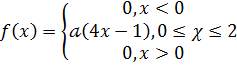
Решение:
Найдем
из условия, что 
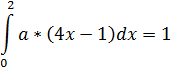
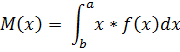
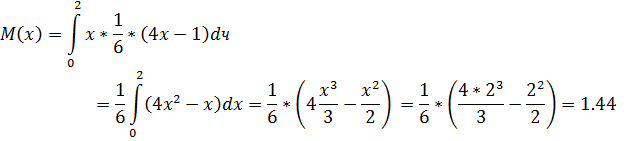
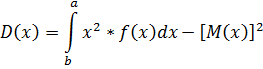
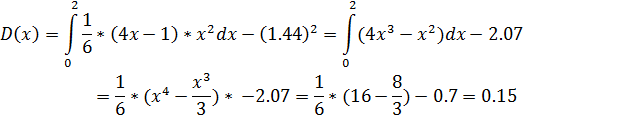
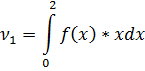
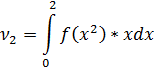
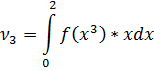
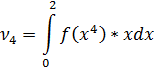
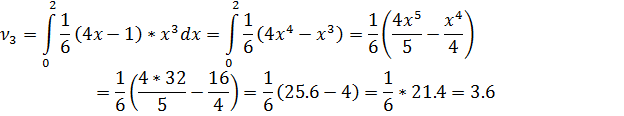
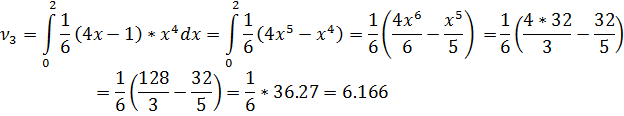
Ответ:
, 
, 
Задача №4
Имеется 400 одинаковых микросхем, включенных параллельно в состав каскада аппаратуры. Время безотказной работы i-й микросхемы T, имеет показательное распределение, одинаковое для всех микросхем (
, и измеряется в часах. При отказе i-й микросхемы каскад автоматически переключается на (i+1) -ю микросхему. Если отказали все микросхемы, то каскад выходит из строя. Выполнить грубую оценку вероятности того, что каскад проработает менее 5500 ч. Каково среднее время работы отдельной микросхемы? Решение:
