Файл: Федеральное государственное автономное образовательное учреждение высшего образования самарский национальный исследовательский университет имени академика с. П. Кор.docx
Добавлен: 09.11.2023
Просмотров: 38
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САМАРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ
ИМЕНИ АКАДЕМИКА С.П. КОРОЛЕВА»
Институт двигателей и энергетических установок
Кафедра теории двигателей летательных аппаратов имени В.П. Лукачева
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1
Выполнил студент группы 2109-130303D
Маточкин А.С.
Проверил старший преподаватель
Остапюк Я.А.
Оценка:___________________
Самара 2022
Часть №1 – массивы.
Задание №1 – для матриц A и B вычислить.
Для совершения вычислений в Mathcad с помощью функции «Матрица или вектор» (
) вводим матрицы A и B: 
, 
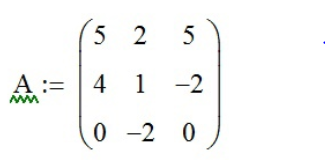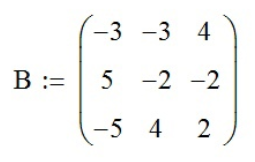;а) 3*А – 2*В - находим значение данного выражения с помощью функции «Рассчитать численно» (
): 
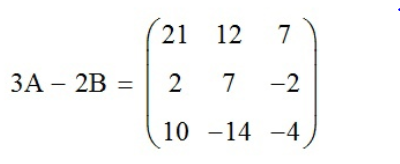;б) A*AT – AT*A - вводим значение AT c помощью функции «Транспонирование матрицы» (
):
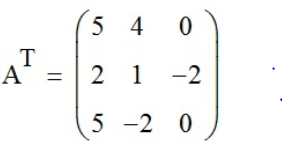; находим значение данного выше выражения с помощью функции «Рассчитать численно» (
):
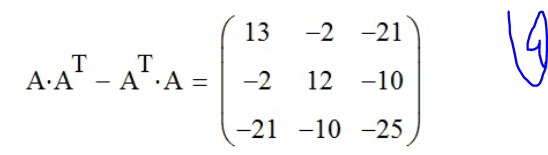.в) A3 - находим значение A3 с помощью функции «Возведение в степень» (
):
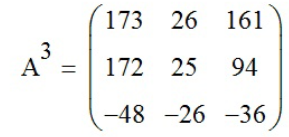.г) 4*A+2*B - находим значение данного выражения функцией «Рассчитать численно» (
):
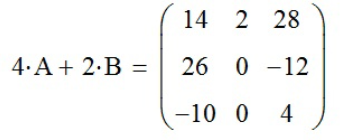.д) A*B - находим значение данного выражения с помощью функции «Рассчитать численно» (
):
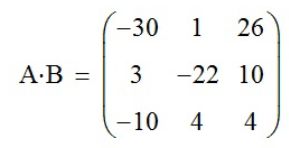.Задание №2 – вычислить определитель матрицы.
С помощью функции «Матрица или вектор» (
) вводим значение указанной матрицы:
;находим её определитель функцией «Определитель» (
):
.Задание №3 – pешить систему линейных уравнений (матричным методом,
по правилу Камера, методом Гаусса).
Чтобы решить данную систему уравнений:
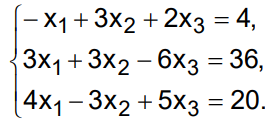
по правилу Крамера, с помощью функции «Матрица или вектор» вводим 3 матрицы (присвоим им значения B, C, D):
,
,
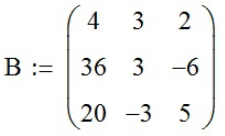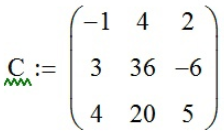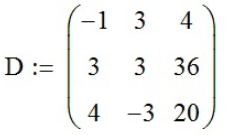.в которых строки составлены из системы уравнений, кроме одного столбца (для каждой из трёх матриц он разный) занимаемого значениями системы уравнений, и 1 матрицу (присвоим ей значение A):
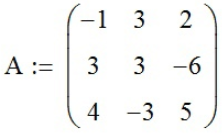,в которой строки составлены из системы уравнений; находим функцией «Определитель» (
) определитель для каждой из четырёх матриц:
,
, 
,
; c помощью функции «Деление» (
) находим значение каждой из трёх неизвестных (x,y,z):
, 
,
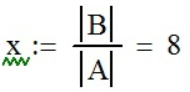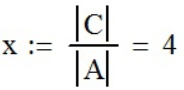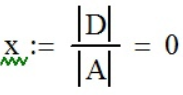.Метод Гаусса:
Для того, чтобы решить систему методом Гаусса, нужно сперва ввести матрицу системы и матрицу-столбец правых частей:
,
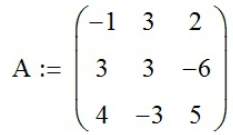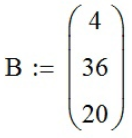;После этого нужно сформировать расширенную матрицу системы. Для того, чтобы сформировать расширенную матрицу системы, нужно использовать функцию augment(A,b), которая формирует матрицу, добавляя к столбцам матрицы системы A справа столбец правых частей b.
Функция rref(Ar) выполняет элементарные операции со строками расширенной матрицы системы Ar-приводит ее к ступенчатому виду с единичной матрицей в первых столбцах, т.е. выполняет прямой и обратный ходы гауссова исключения.
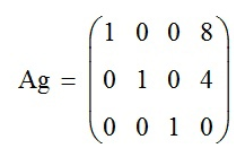
Ответ:
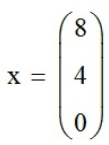
Проверка:
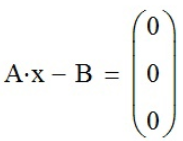
Задание №4 - найти матрицу A-1, обратную данной матрице A, и проверить выполнение условия A*A-1 = E.
Введём матрицу A с помощью функции «Матрица или вектор» (
):
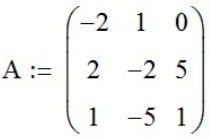;функцией «Обращение» найдём матрицу A-1:
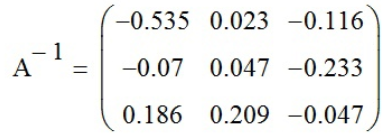;умножим матрицу A на A-1, и так как матрица A-1 обратная матрице A, то A*A-1будет равно E (E – единичная матрица):
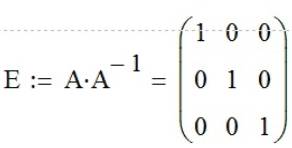.Часть №2 – пределы.
Задание №1 – доказать, что
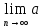n= a.Даны значения an и a:
;найдём предел an(
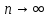) с помощью функции «Двусторонний предел» (
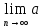) и увидим, что n= a: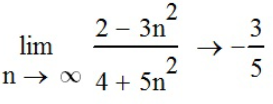
.Задание №2 - найти пределы алгебраических функций.
Зададим все четыре предела с помощью функции «Двусторонний предел» (
) и найдём их функцией «Вычислить аналитически» (
):
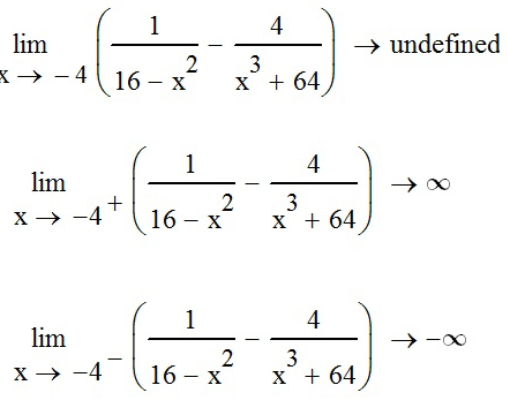
Задание №3 - найти пределы тригонометрических функций.
Зададим все шесть пределов с помощью функций панели инструментов «Калькулятор» (
), так как функции тригонометрические, и функцией «Двусторонний предел» (
) и вычислим пределы с помощью функции «Вычислить аналитически» (
):
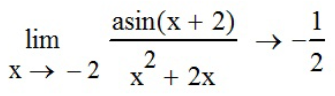
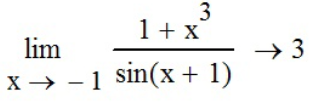
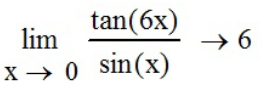
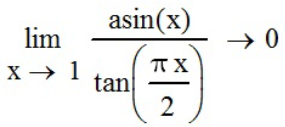
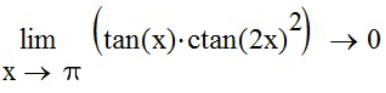
Задание №4 - найти пределы показательно-степенных функций
Зададим все четыре предела с помощью функций панели инструментов «Калькулятор» (
), так как функции показательные, и функцией «Двусторонний предел» ( ); найдём их с помощью функции «Вычислить аналитически» ( ):
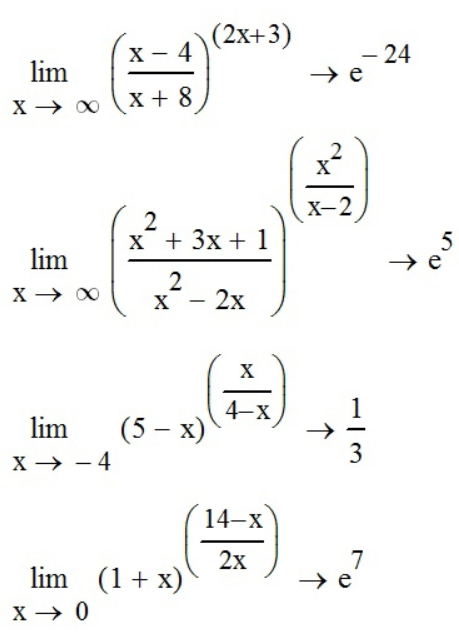.Задание №5 - исследовать функцию на непрерывность, найти и классифицировать точки разрыва. Построить эскиз графика функции вблизи точек разрыва.
№1) Зададим функцию с помощью функций панели инструментов «Калькулятор» (