Файл: Федеральное государственное автономное образовательное учреждение высшего образования самарский национальный исследовательский университет имени академика с. П. Кор.docx
Добавлен: 09.11.2023
Просмотров: 39
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
) и найдём ОДЗ:
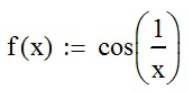 ;
;
посредством функции «График» ( ) получаем график функции:
) получаем график функции:
 .
.
№2) Зададим функцию с помощью функций панели инструментов «Калькулятор» ( ) и найдём ОДЗ:
) и найдём ОДЗ:
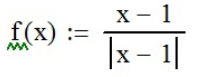 ;
;
находим пределы справа и слева для точек подозрительных на разрыв с помощью функций «Предел справа» ( ) и «Предел слева» (
) и «Предел слева» ( ):
):
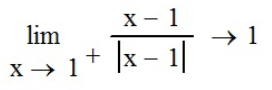 ,
, 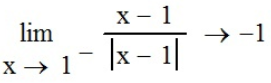 ;
;
посредством функции «График» ( ) получаем график функции:
) получаем график функции:
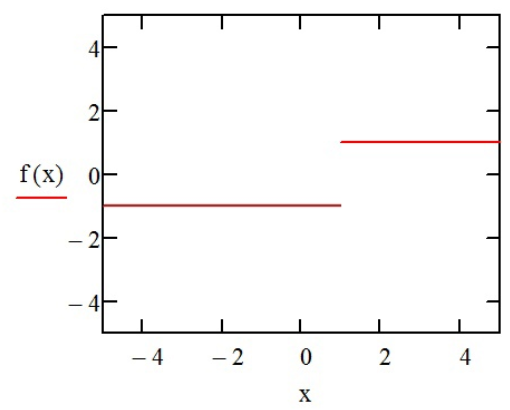
Часть №3 – производные
Задание №1 - Составить уравнения нормали и касательной к данной кривой в точке с абсциссой x0.
Зададим функцию y(x) и x0 (которая для удобства названа a):
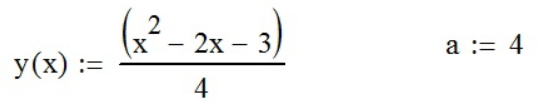 ;
;
вычислим уравнение касательной посредством формулы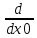 y(x0)*(x-x0)+y(x0) и функции«Вычислить аналитически» (
y(x0)*(x-x0)+y(x0) и функции«Вычислить аналитически» ( ):
):
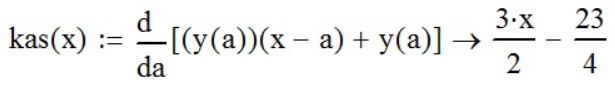 ;
;
вычислим уравнение нормали с помощью формулы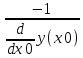
*(x-x0)+y(x0) и функции«Вычислить аналитически» ( ):
):
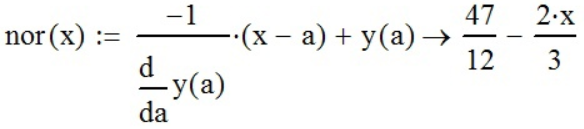 ;
;
функцией «График» получаем график функции и касательной, и нормали:
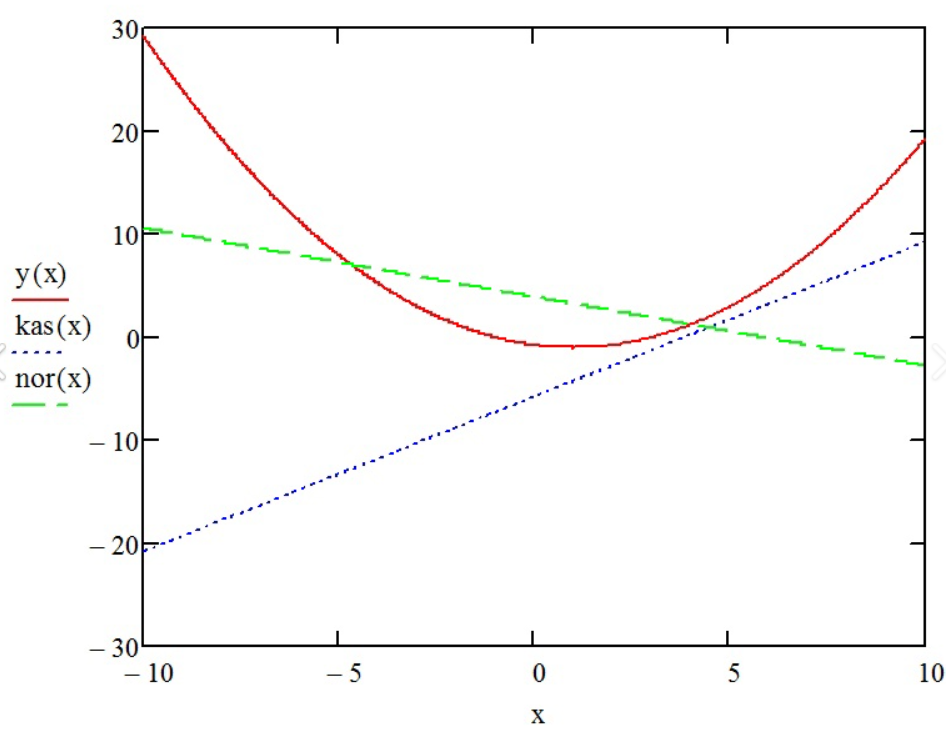 .
.
Задание №2 - найти дифференциал dy.
Зададим функцию функциями панели инструментов «Калькулятор» ( ):
):
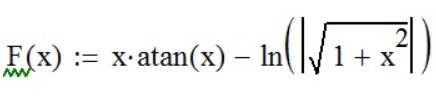 ;
;
продифференцируем функцию с помощью «Производной» (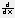 ) и «Вычислить аналитически» (
) и «Вычислить аналитически» ( ):
):
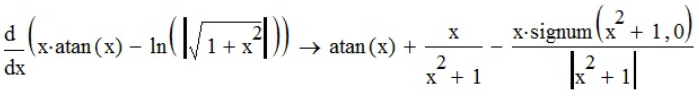 .
.
Задание №3 - Найти производную.
Зададим функцию функциями панели инструментов «Калькулятор» ( ):
):
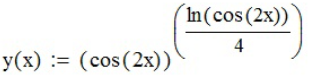 ;
;
продифференцируем функцию с помощью «Производной» (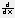 ), «Вычислить аналитически» (
), «Вычислить аналитически» ( ):
):
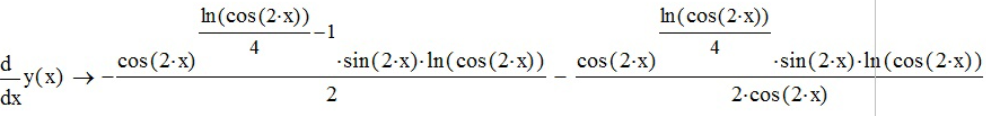 .
.
Задание №4 - Найти производную yx’.
Зададим функцию функциями панели инструментов «Калькулятор» ( ):
):
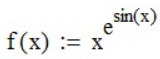 ;
;
продифференцируем функцию с помощью «Производной» (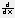
), «Вычислить аналитически» ( ):
):
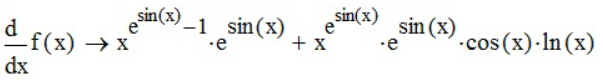 .
.
Задание №5 - Найти производную y’x и упростить выражение.
Зададим функцию функциями панели инструментов «Калькулятор» ( ):
):
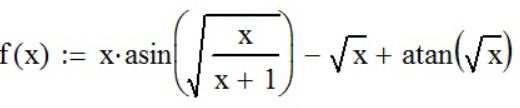 ;
;
продифференцируем функцию с помощью «Производной» ( ), «Вычислить аналитически» (
), «Вычислить аналитически» ( ) и упростим её функцией «simplify»:
) и упростим её функцией «simplify»:
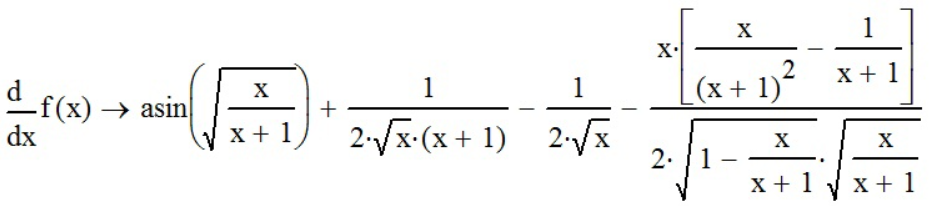
Задание №6 - Найти производную y’x.
Зададим неявную функцию как функцию F(x,y) с помощью панели инструментов «Калькулятор» ( ):
):
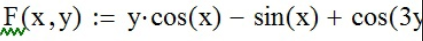 ;
;
продифференцируем функцию по x и y с помощью «Производной» ( ) и «Вычислить аналитически» (
) и «Вычислить аналитически» ( ):
):
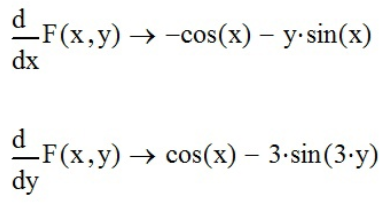 ;
;
так как y’x=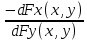 , найдём значение производной посредством «Деления» (
, найдём значение производной посредством «Деления» ( ) и «Вычислить аналитически» (
) и «Вычислить аналитически» ( ) и simplify:
) и simplify:
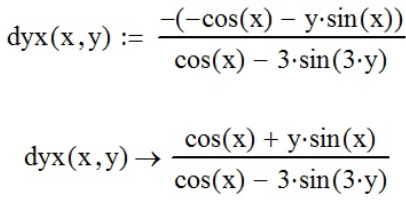 .
.
Задание №7 - Найти производную yx’.
Зададим систему уравнений с помощью панели инструментов «Калькулятор» (
 ):
):
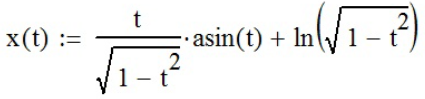
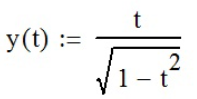 ;
;
продифференцируем функции x(t) и y(t) с помощью «Производной» ( ) и «Вычислить аналитически» (
) и «Вычислить аналитически» ( ):
):
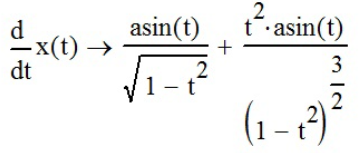
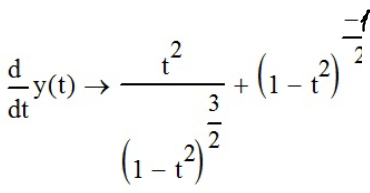 ;
;
так как y’x=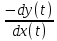 , найдём значение производной посредством «Деления» (
, найдём значение производной посредством «Деления» ( ) и «Вычислить аналитически» (
) и «Вычислить аналитически» ( ):
):
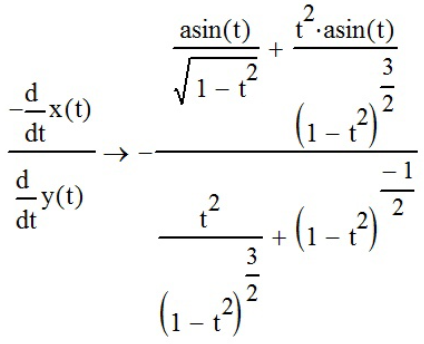 .
.
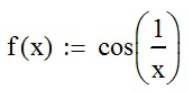 ;
; посредством функции «График» (
 .
.№2) Зададим функцию с помощью функций панели инструментов «Калькулятор» (
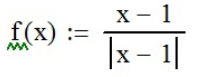 ;
; находим пределы справа и слева для точек подозрительных на разрыв с помощью функций «Предел справа» (
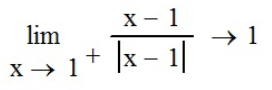 ,
, 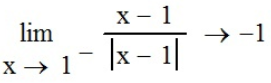 ;
; посредством функции «График» (

Часть №3 – производные
Задание №1 - Составить уравнения нормали и касательной к данной кривой в точке с абсциссой x0.
Зададим функцию y(x) и x0 (которая для удобства названа a):
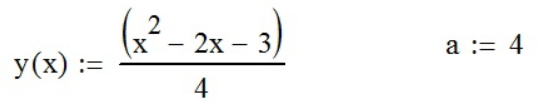 ;
; вычислим уравнение касательной посредством формулы
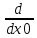 y(x0)*(x-x0)+y(x0) и функции«Вычислить аналитически» (
y(x0)*(x-x0)+y(x0) и функции«Вычислить аналитически» (вычислим уравнение нормали с помощью формулы
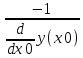
*(x-x0)+y(x0) и функции«Вычислить аналитически» (
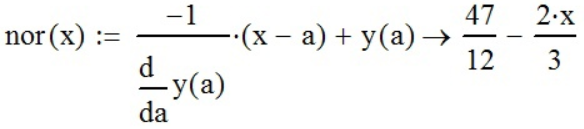 ;
; функцией «График» получаем график функции и касательной, и нормали:
 .
.Задание №2 - найти дифференциал dy.
Зададим функцию функциями панели инструментов «Калькулятор» (
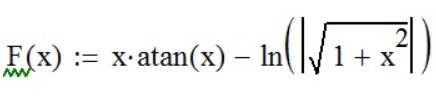 ;
; продифференцируем функцию с помощью «Производной» (
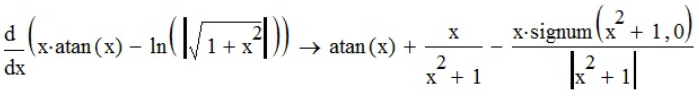 .
. Задание №3 - Найти производную.
Зададим функцию функциями панели инструментов «Калькулятор» (
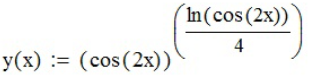 ;
;продифференцируем функцию с помощью «Производной» (
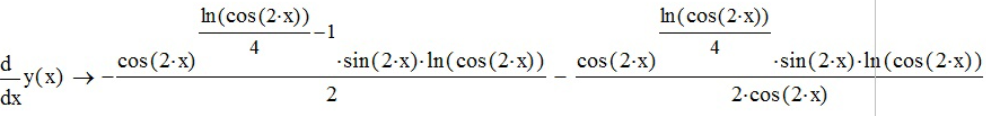 .
.Задание №4 - Найти производную yx’.
Зададим функцию функциями панели инструментов «Калькулятор» (
продифференцируем функцию с помощью «Производной» (
), «Вычислить аналитически» (
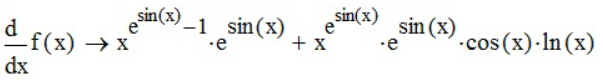 .
. Задание №5 - Найти производную y’x и упростить выражение.
Зададим функцию функциями панели инструментов «Калькулятор» (
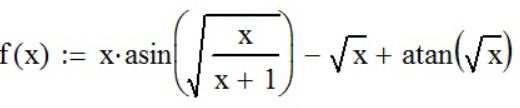 ;
;продифференцируем функцию с помощью «Производной» (
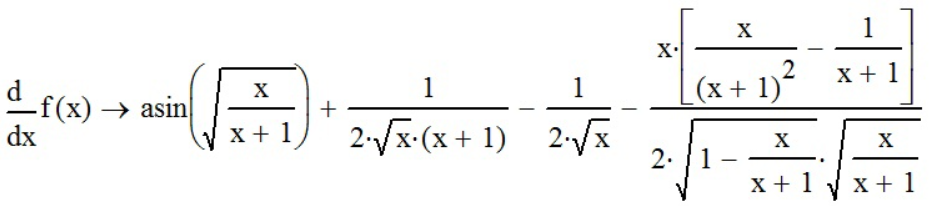
Задание №6 - Найти производную y’x.
Зададим неявную функцию как функцию F(x,y) с помощью панели инструментов «Калькулятор» (
продифференцируем функцию по x и y с помощью «Производной» (
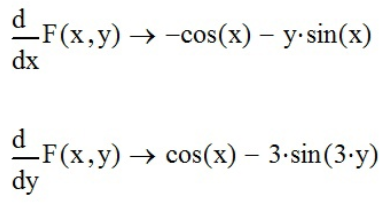 ;
; так как y’x=
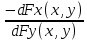 , найдём значение производной посредством «Деления» (
, найдём значение производной посредством «Деления» (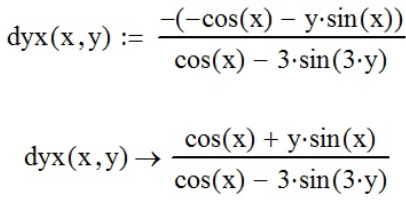 .
.Задание №7 - Найти производную yx’.
Зададим систему уравнений с помощью панели инструментов «Калькулятор» (
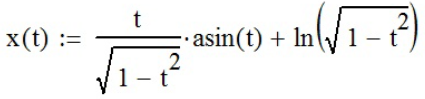
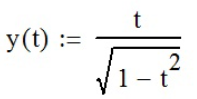 ;
; продифференцируем функции x(t) и y(t) с помощью «Производной» (
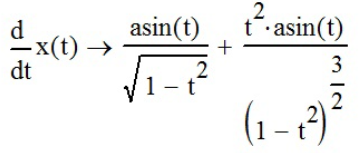
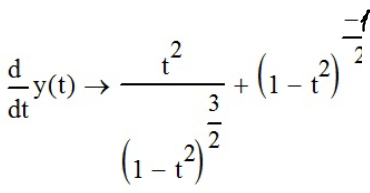 ;
; так как y’x=
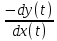 , найдём значение производной посредством «Деления» (
, найдём значение производной посредством «Деления» (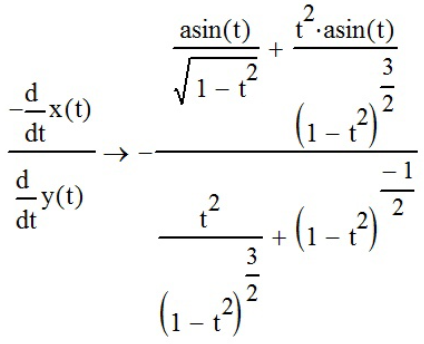 .
.