ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

ФИНАНСОВЫЙ УНИВЕРСИТЕТ

ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ

(Пензенский филиал)
Кафедра «Менеджмент, информатика и общегуманитарные науки»

Направление «Менеджмент»

КОНТРОЛЬНАЯ РАБОТА
по дисциплине

«Количественные методы в менеджменте»

Вариант 6.

Студент Черных Виктория Андреевна

Курс 2 № группы ПНЗ21-1Б-ФМ2

Личное дело № 100.21/210126

Преподаватель Н.А. Кривошеева


Пенза – 2023

ЗАДАЧА 1

Для изготовления трех видов изделий используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.

Тип сырья	Нормы расхода сырья на одно изделие			Запасы сырья
	А	Б	В
I	18	15	12		360
II	6	4	8		192
III	5	3	3		180
Цена изделия	9	10	16

Обозначим через 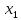, , 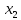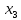объемы производства соответствующего вида продукции.

---

Получим: – объем производства продукции А, – объем производства продукции Б, – объем производства продукции В, 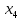– объем производства продукции Г.

1) Экономико-математическая модель задачи «максимум выручки от реализации готовой продукции» имеет вид:











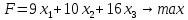
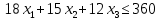
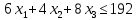
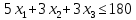
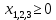
Далее решаем задачу с помощью надстройки Excel «поиск решений».
Создаем таблицу и вводим в нее исходные данные задачи. Затем вводим зависимость для целевой функции в ячейке F4 и зависимости для ограничений в ячейки F7, F8, F9:



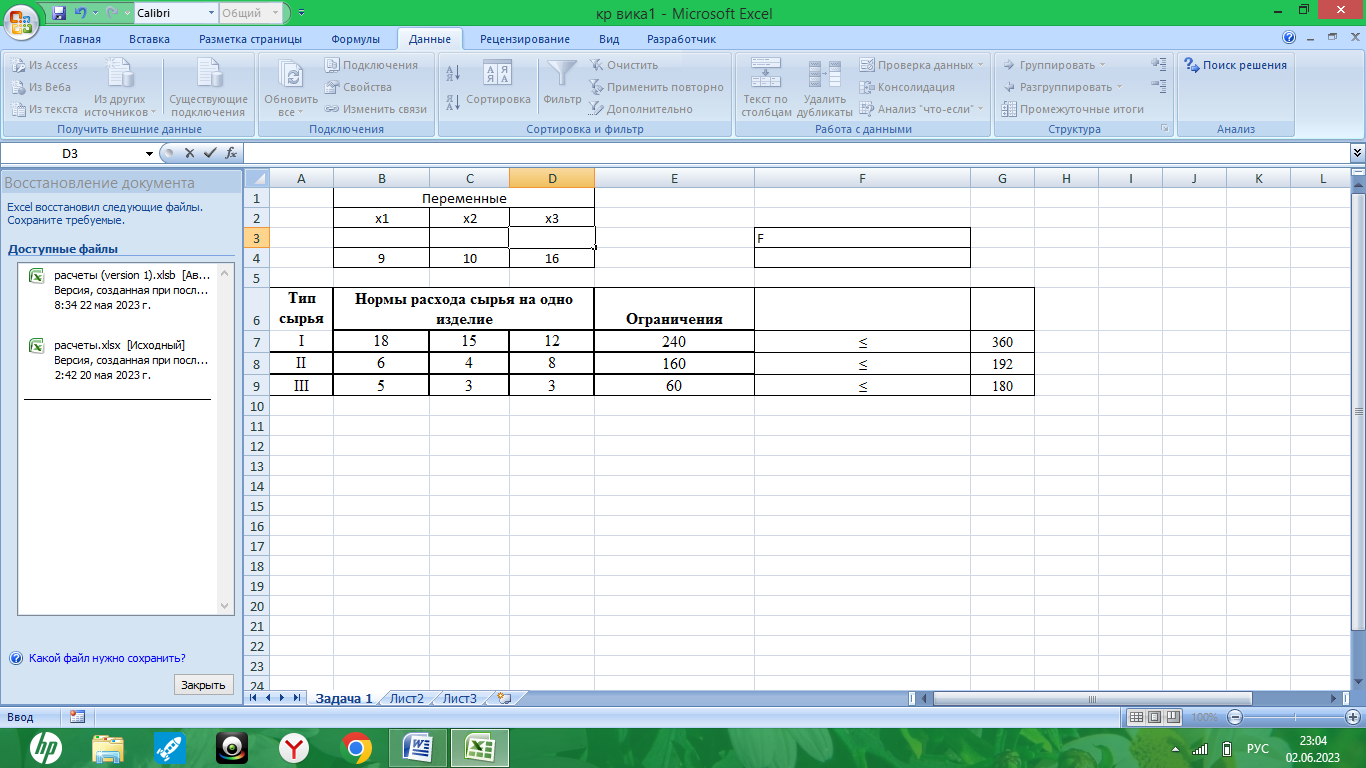
Рис. 1. – Формулы целевой функции и ограничений

В развернутом меню команда «поиск решения» устанавливаем целевую ячейку, вводим данные по направлению целевой функции, заполняем строку «изменяя ячейки» и вводим ограничения:



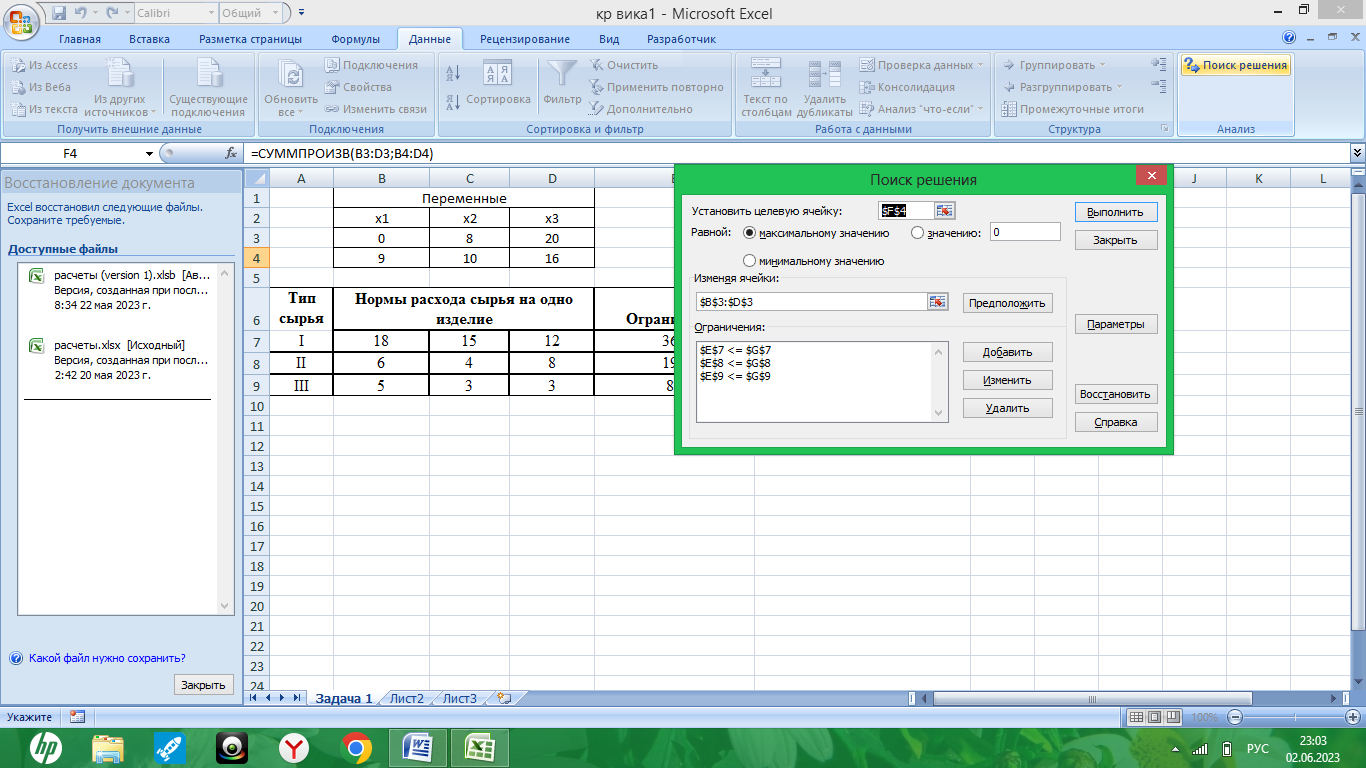
Рис. 2. – Параметры поиска решения

Сохраняем найденное решение:



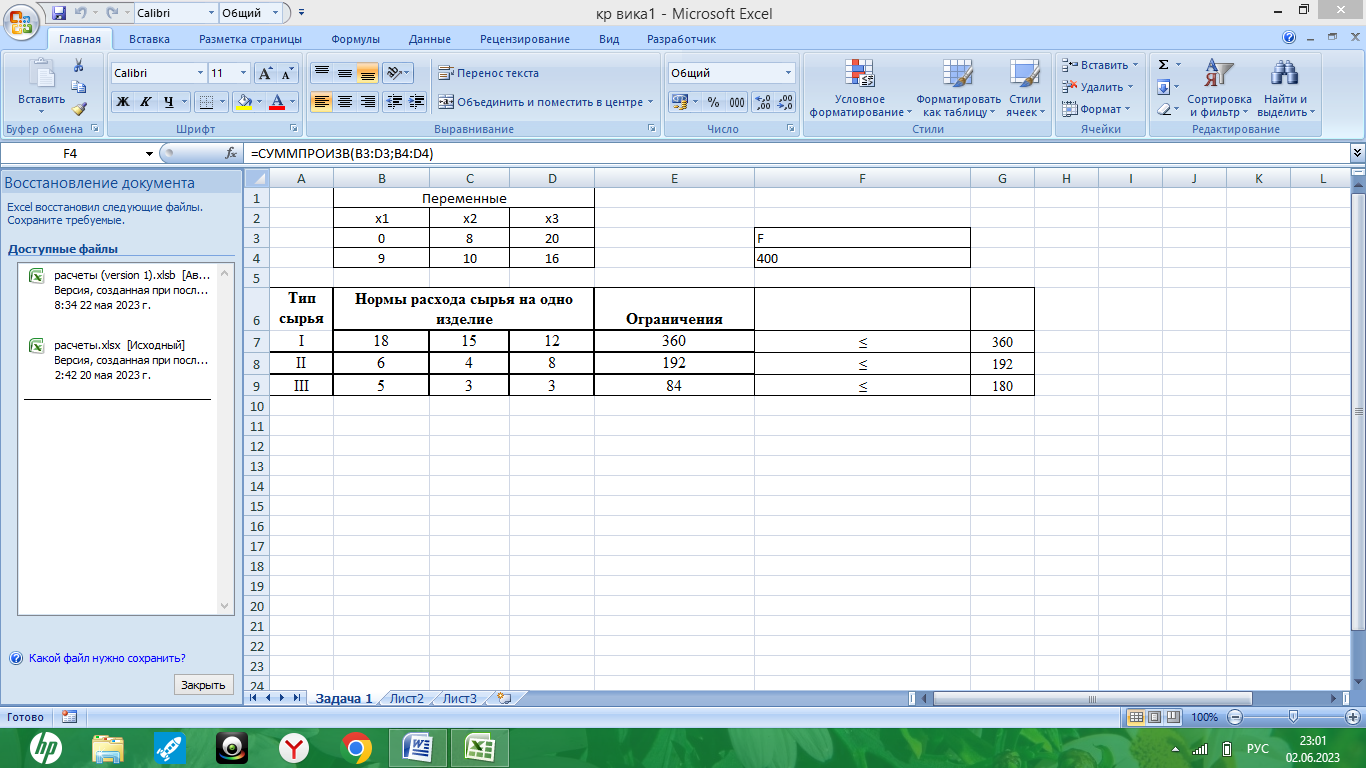
Рис. 3. – Результаты поиска решения

Продукция Б и В не рентабельна (Х1=0). Продукцию видов А и Г выгодно производить в количествах соответственно равных 8 и 20. При таком плане производства продукции выручка от реализации готовой продукции будет максимальна и составит 400 ден.ед.

Составим двойственную задачу:

y₁ – цена за единицу сырья 1 типа,

y₂ – цена за единицу сырья 2 типа,

y₃ – цена за единицу сырья 3 типа.

---

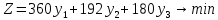
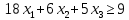
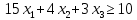
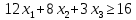
Создадим отчет об устойчивости и по нему найдем решение задачи.


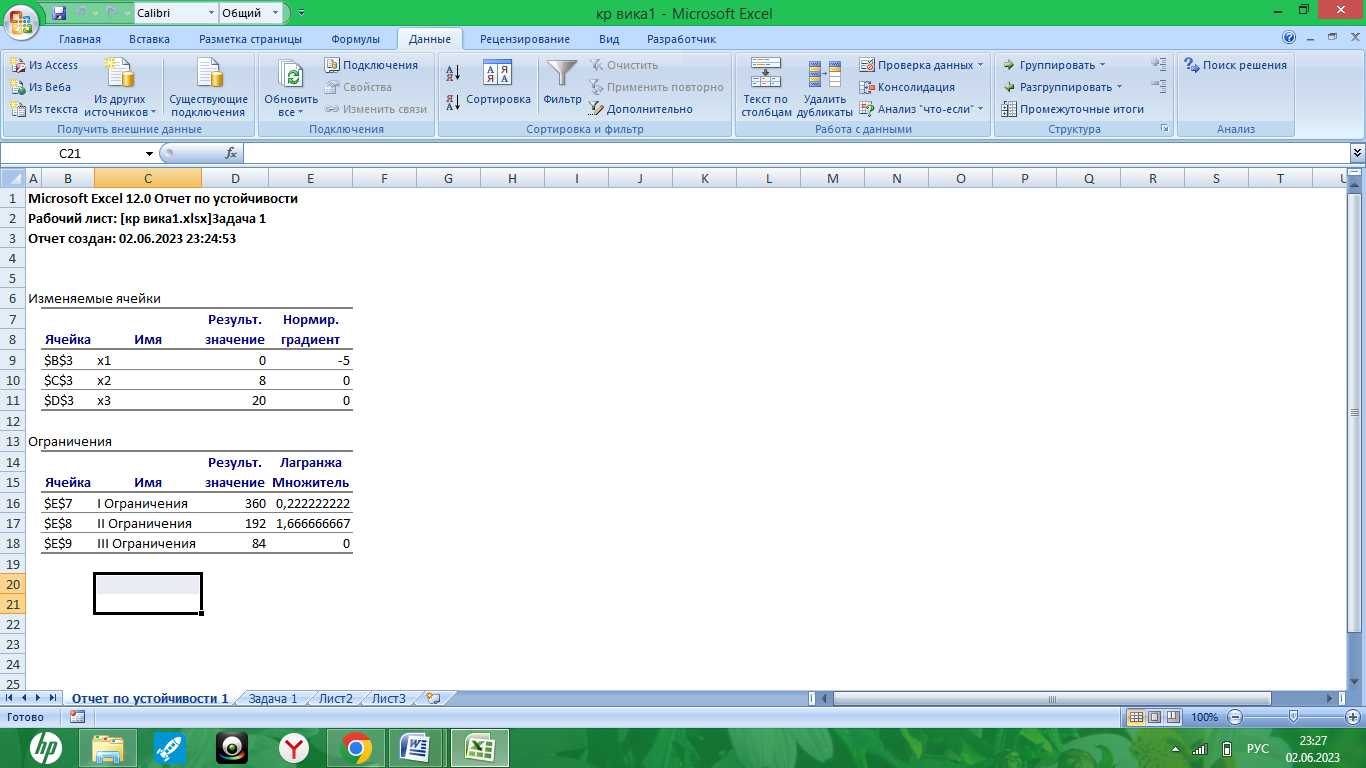
Рис. 4. – Отчет об устойчивости

В столбце «теневая цена» мы видим:

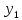= 0 – цена на 1 единицу I типа сырья;

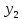= 8 – цена на 1 единицу II типа сырья;

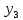= 20 – цена на 1 единицу III типа сырья.

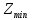= 400 – минимальные общие затраты на ресурсы.

= .

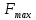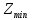Экономический смысл: предприятию безразлично производить ли продукцию по оптимальному плану Х и продавать ее с максимальной прибылью 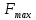или продавать ресурсы по оптимальным ценам У, возмещая от продажи общие минимальные затраты на них 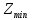равные .

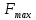Нулевые значения переменной в оптимальном плане 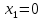, означает, что продукцию данного вида выпускать нецелесообразно.
ЗАДАЧА 2.

Исходные данные транспортной задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху - мощности потребителей. Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя Поиск решения.X	40	30	90	80	50
60	4	2	3	4	1
90	2	4	3	5	6
140	6	5	4	6	2

---

Искомый объем перевозки от i-ого поставщика к j-ому потребителю обозначим через 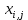, i, j = 1, 2, 3. Тогда определяются ограничения для условия реализации всех мощностей: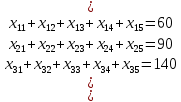



Общий объем поставок 60+90+140=290.

Ограничения для удовлетворения спросов всех потребителей:



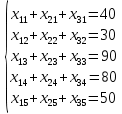
Общие потребности 40+30+90+80+50=290.

Задача имеет сбалансированную (закрытую) форму (объем поставок равен спросу).

Очевидно, что объем перевозимого груза не может быть отрицательным, поэтому следует ввести дополнительное ограничение: .

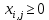Суммарные затраты на перевозку выражаются через удельные транспортные затраты и определяют целевую функцию.



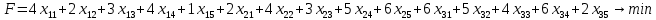
Итак, получили задачу минимизации транспортных затрат:



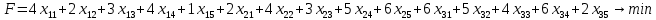
При ограничениях:





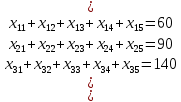
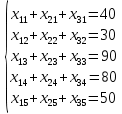
Табличная модель.

Вводим данные в таблицу Excel:



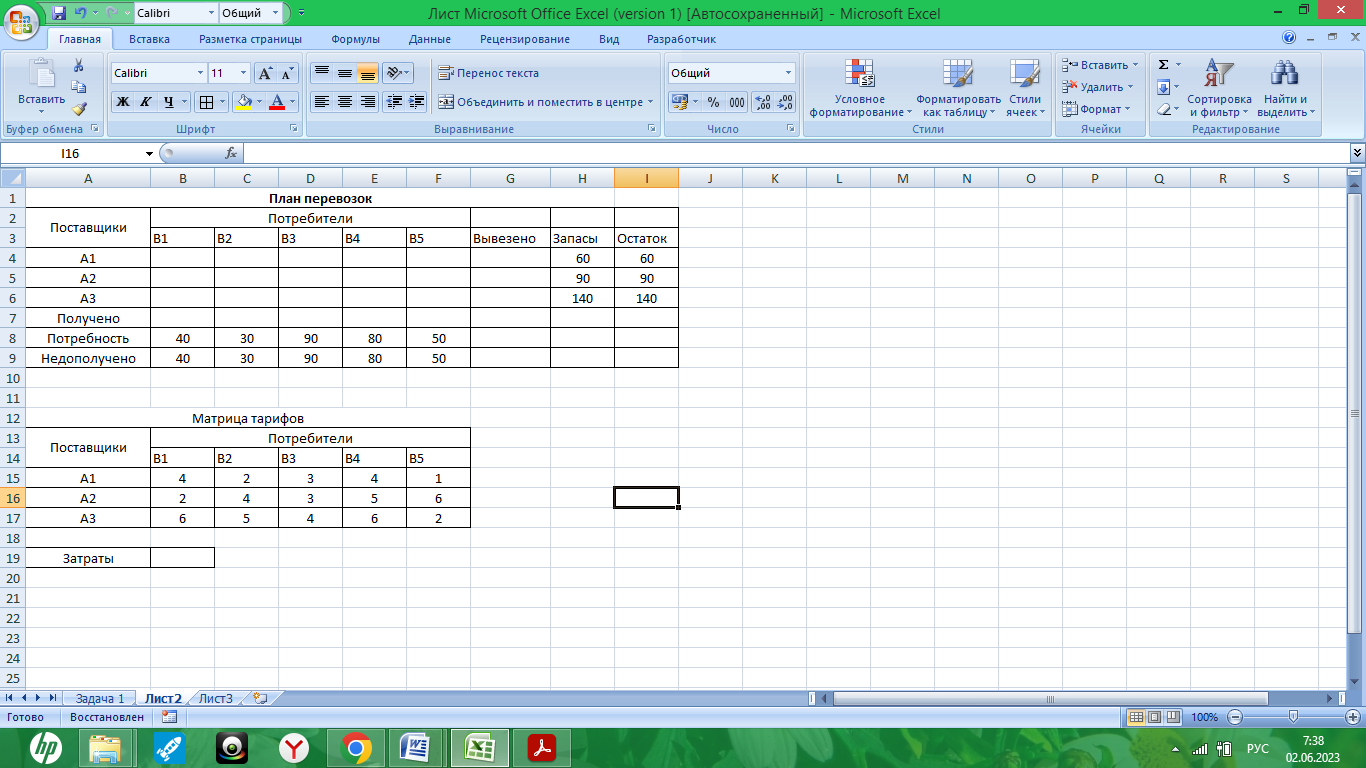
Рис. 7. – Табличное представление модели задачи



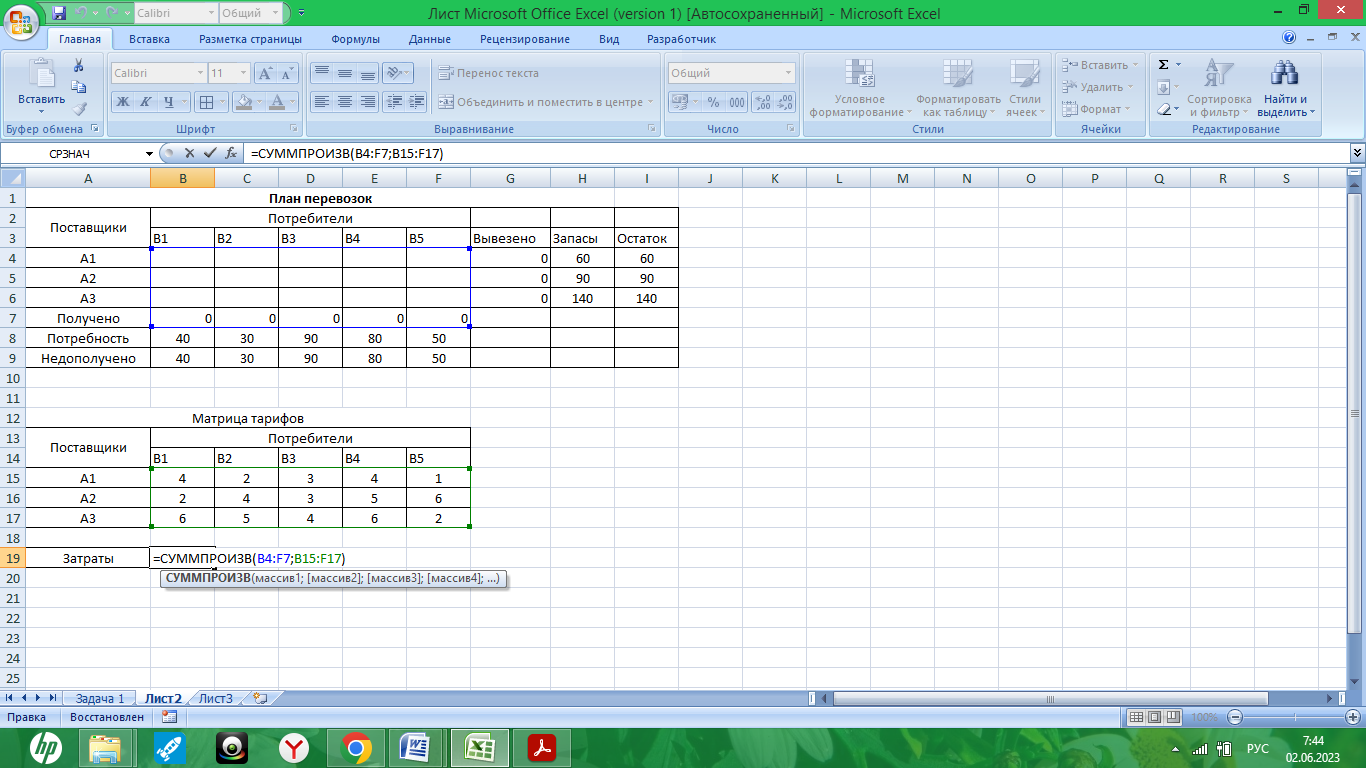
Рис. 8. – Табличная модель с формулами

С помощью надстройки Поиск решения находим оптимальный план закрепления поставщиков за потребителями.



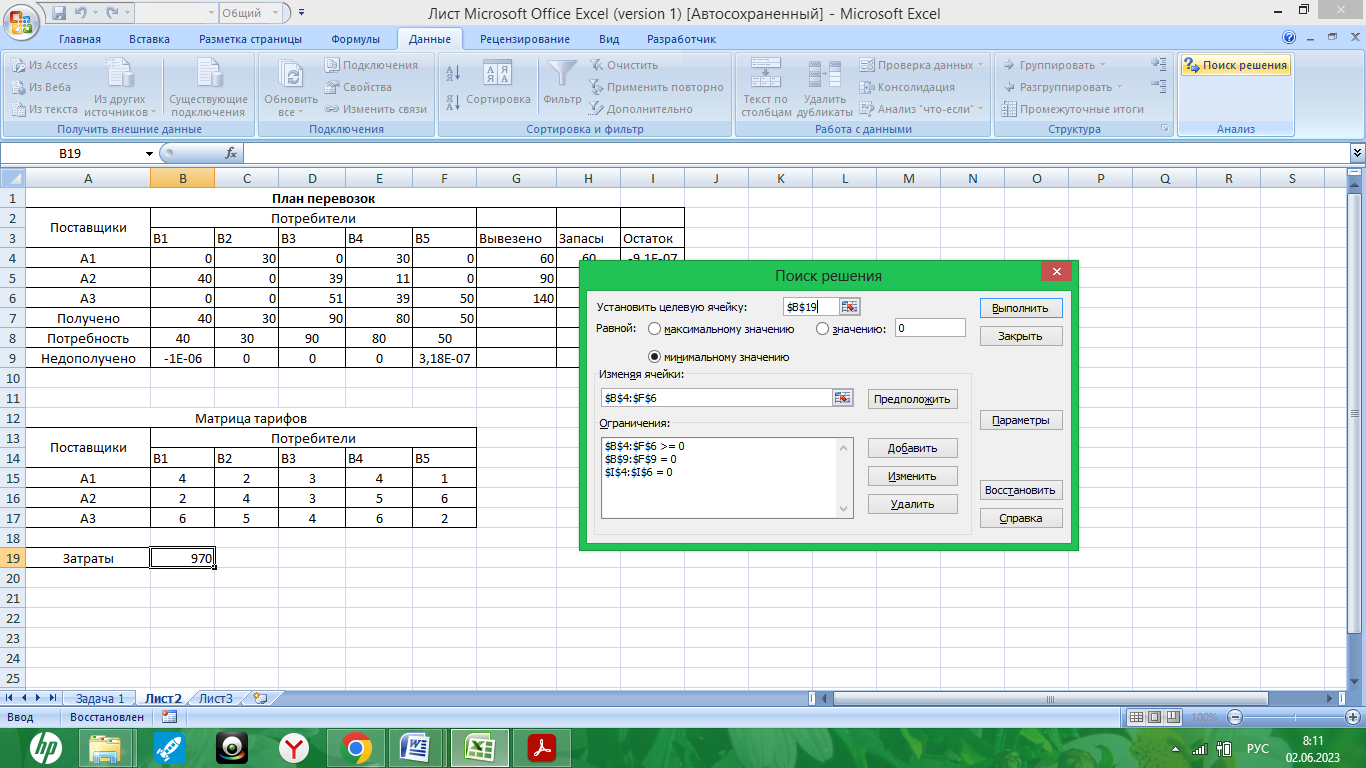
Рис. 9. – Диалоговое окно надстройки Поиск решения



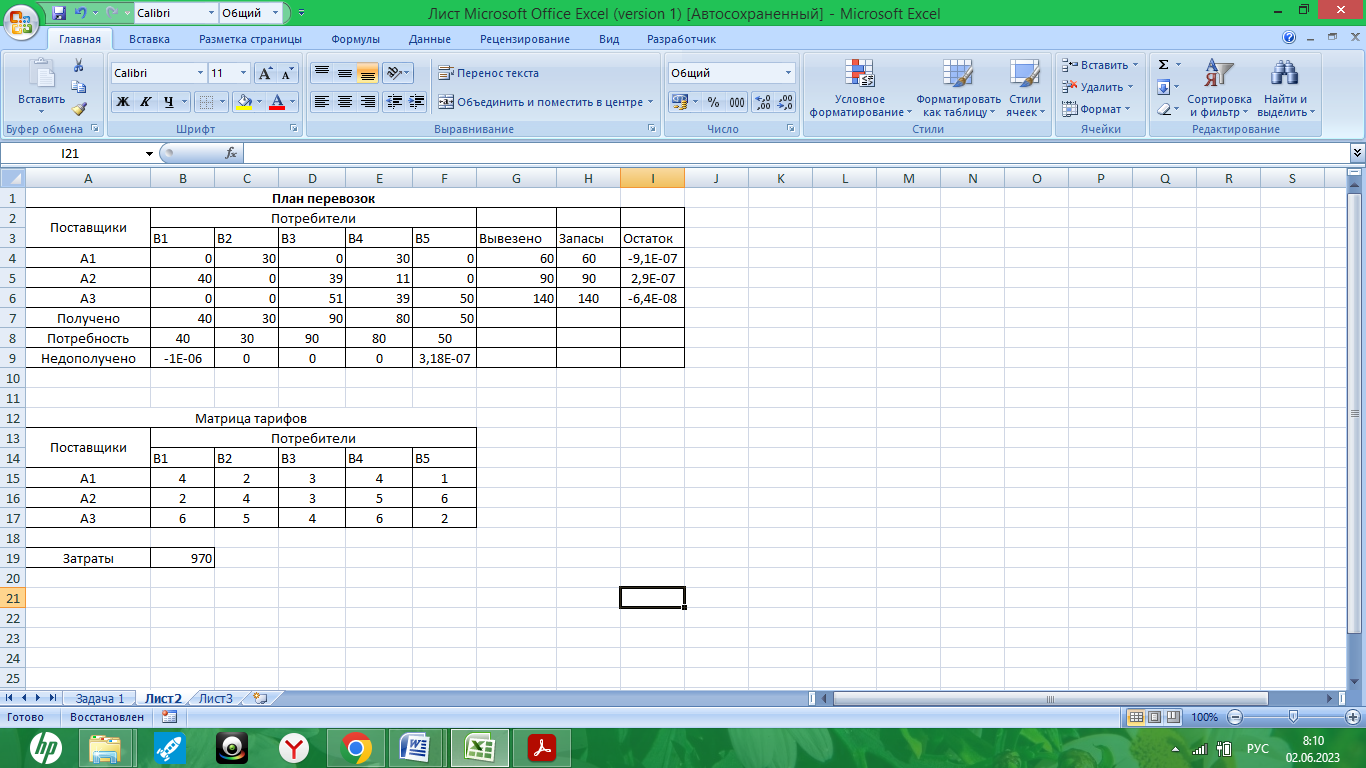
Рис. 10. – Решение транспортной задачи

Вывод: Минимальные суммарные затраты на перевозку груза равны 970 ден.ед. Они достигаются путем распределения поставок, представленных в ячейках [B4:E7]. Так, например, поставщик А1 должен доставить груз только потребителю В4 в количестве 30 единиц. Поставщик А2 должен поставить груз к потребителю В1 в количестве 40 ед., к потребителю В3 – 39 ед., В4 -11 ед. Поставщик А3 должен доставить груз только потребителю В3 в количестве 51 ед., В4 – 39 ед. и В5 – 50ед.

---

ЗАДАЧА 3

Торговая организация решила закупить партию сезонных товаров. У нее имеются 4 коммерческих предложения от разных поставщиков: А, Б, В и Г. Прибыль организации зависит от возможного спроса на каждую предлагаемую продукцию. Отдел маркетинга прогнозирует 4 возможные величины спроса: С1, С2, С3, С4. Прибыль по каждому предложению для каждого варианта спроса представлена в табл. 1.

А) Используя критерии Лапласа, Вальда, метод максимального оптимизма, Сэвиджа, Гурвица при α = р, принять оптимальное решение по выбору поставщика.

Б) Определить оптимальную стратегию при известном векторе Р вероятностей состояний спроса.

	С1	С2	С3	С4
А	112	115	135	142
Б	102	125	135	140
В	105	123	136	138
Г	104	114	134	144

p = 0,3; P = (0,3; 0,2; 0,4; 0,1;)

Решение:

А) 1. Критерий Лапласа. Показателем эффективности чистой стратегии Аi по критерию Лапласа относительно выигрышей является среднеарифметическое выигрышей при этой стратегии.

Для поставщика А:

1. 
   = (112 + 115 + 135 + 142) / 4 = 126
   

Для поставщика Б:

(Б) = (102 + 125 + 135 + 140) / 4 = 125,5

Для поставщика В:

(В) = (105+ 123 + 136 + 138) / 4 = 125,5

Для поставщика Г:

(Г) = (140 + 114 + 134 + 144) / 4 = 124

L = max (126, 125,5, 125.5, 124) = 126

Полученный результат соответствует поставщику А.

2. Критерий Вальда. Критерий Вальда (критерий гарантированного

результата, максиминный критерий) позволяет выбрать наибольший элемент матрицы доходности из её минимально возможных элементов.

Для поставщика А:

(A) = min (112, 115, 135, 142) = 112

Для поставщика Б:

(Б) = min (102, 125, 135,140) = 102

Для поставщика В:

(В) = min (105, 123, 136, 138) = 105

Для поставщика Г:

(Г) = min (104, 114, 134, 144) = 104

W = max (112, 102, 105, 104) = 102

Полученный результат соответствует поставщику Б.

3. Метод максимального оптимизма. Критерий оптимизма (критерий максимакса) предназначен для выбора наибольшего элемента матрицы доходности из её максимально возможных элементов.

---

Смотрите также файлы

• Сравнение данных плотностного каверномера в бурении и обратной проработке Скважина 81 Загрузите из ласфайла 81 каротаж память прибора.docx

• Лекция Общее понятие об ощущении План.pdf

• Учебник для медицинских училищ и колледжей в тор о е издание вт. Пальчун болезни уха горла и носа уч ебни к для медицинских училищ и колледжей.pdf

• Реализации тактических управленческих решений.docx

• Удк 616002. 5022. 7053. 2 Роль скрининговых обследований детского населения на туберкулезную инфекцию.pdf