ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 69
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
ИНСТИТУТ ФИНАНСОВ, ЭКОНОМИКИ И УПРАВЛЕНИЯ
(наименование института полностью)
Департамен баклавариата экономических и управленческих программ
(наименование кафедры/департамента/центраполностью)
38.03.01 Экономика
(код и наименование направления подготовки, специальности)
Бухгалтерский учет, анализ и аудит
(направленность (профиль) / специализация)
Практическое задание №1
по учебному курсу «Микроэкономика»
(наименование учебного курса)
Вариант ____ (при наличии)
| Студент | (И.О. Фамилия) | |
| Группа | (И.О. Фамилия) | |
| Преподаватель | (И.О. Фамилия) | |
Тольятти 2022
Бланк выполнения практического задания 1
Задача 1
Кривая индивидуального спроса на некоторое благо линейна и при цене
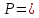 40, эластичность спроса по цене
40, эластичность спроса по цене 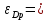 –4 . Достижение какого уровня цены
–4 . Достижение какого уровня цены 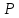 приведет к полному отказу от потребления этого товара?
приведет к полному отказу от потребления этого товара? Решение
-
Линейная функция спроса имеет вид:
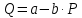 . (1.1)
. (1.1)-
Коэффициент эластичности спроса по цене определяется по формуле:
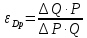 , (1.2)
, (1.2)-
Из формулы 1.1 выводится условие изменения в объеме спроса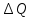 (Полученное условие указывают в решении) и коэффициент
(Полученное условие указывают в решении) и коэффициент 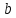 .
.
∆Q=a-b∙∆P
-
В формулу 1.2 подставляются значения коэффициента и определяется значение коэффициента
и определяется значение коэффициента 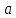 .
.
b∙P=a-Q;
b=a-QP;
-
Определяется значение , при котором
, при котором 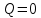 , используя преобразованную функцию спроса и данные из условия.
, используя преобразованную функцию спроса и данные из условия.
Edp = P/(Pmax – P)
где Pmax – максимальная цена
Ответ: 60 рублей, т.е. достижение этой цены приведет к полному отказу от потребления этого товара.
Задача 2
Функция спроса на товар имеет вид
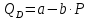 . При каких значениях цены товара кривая спроса эластична? На графике покажите эластичный и неэластичные участки кривой спроса
. При каких значениях цены товара кривая спроса эластична? На графике покажите эластичный и неэластичные участки кривой спроса 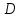 .
.Решение
-
По формуле 1.2 определяется единичная эластичность спроса. -
В формулу 1.2 подставляются значения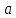 и
и  .
. -
Рассчитывается цена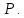
-
Эластичный участок расположен в 2,1 кривой спроса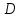 .
.
Бланк выполнения практического задания 2
Задача
Предположим, что доход потребителя в месяц составляет
 руб. на потребительский набор
руб. на потребительский набор 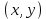 . Цена единицы товара
. Цена единицы товара 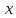 равна
равна 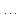 руб., а цена единицы товара
руб., а цена единицы товара 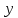 равна
равна 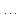 руб.
руб. 1. Запишите бюджетное ограничение (БО) потребителя и покажите на графике соответствующее бюджетное множество (БМ).
2. Изменения в экономике привели к необходимости ввести налог на цену товара
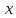 . Теперь каждая единица товара
. Теперь каждая единица товара
 будет обходиться всем потребителям на
будет обходиться всем потребителям на 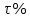 дороже. Запишите БО для этого случая и покажите на графике соответствующее БМ. Что произошло со множеством доступных потребителю наборов после ограничительной политики правительства?
дороже. Запишите БО для этого случая и покажите на графике соответствующее БМ. Что произошло со множеством доступных потребителю наборов после ограничительной политики правительства?3. В результате введения правительством налога на цену товара администрацией региона была введена потоварная субсидия на товар
 , равная сумме
, равная сумме 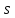 руб. Запишите БО для этого случая и покажите графически БМ. Как изменилось бюджетное множество потребителя по сравнению с начальным вариантом?
руб. Запишите БО для этого случая и покажите графически БМ. Как изменилось бюджетное множество потребителя по сравнению с начальным вариантом?Решение:
-
Бюджетное ограничение по заданным значениям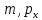 и
и 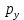 принимает вид: … .
принимает вид: … .
Графический вид бюджетного множества представлен на рисунке 2.1.
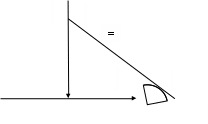
Рис. 2.1. Бюджетное множество потребителя
-
Введение налога на стоимость товара привело к изменению цены
привело к изменению цены 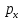 . Фактическая цена составила 48 руб. Бюджетное ограничение принимает вид: 48x+50y ≤ 800.
. Фактическая цена составила 48 руб. Бюджетное ограничение принимает вид: 48x+50y ≤ 800.
Бюджетные множества представлены на рисунке 2.2.
800/48=16.7 Qx Qy 800/50=16 mpy mpx y x m= -pxpy
Вывод: Вывод: после поднятия цены на 20 % на товар х, потребитель сможет приобрести максимально 16,7 единиц товара х..
-
Сохраняя условия п. 2, администрация региона ввела потоварную субсидию на товар в размере
в размере 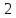 руб. Фактическая цена составила 48 руб. Бюджетное ограничение принимает вид: 48х + 58у ≤ 800.
руб. Фактическая цена составила 48 руб. Бюджетное ограничение принимает вид: 48х + 58у ≤ 800.
Бюджетные множества представлены на рисунке 2.3.
800/48=16.7 Qx Qy 800/48=16,7 mpy mpx y x m= -pxpy.
Вывод: теперь потребитель сможет приобрести товара У в максимальном количестве 16,7 единиц или товара Х также в размере 16,7 единиц. Условия пунктов 2 и 3 отменены.
-
Условия пунктов 2 и 3 отменены. Магазин ввел следующую систему скидок: 20. Для нахождения бюджетного ограничения решаем систему уравнений: 48х + 58у ≤ 800.
Бюджетные множества представлены на рисунке 2.4.
……………………………………………………………………………
Вывод: … .
Бланк выполнения практического задания 3
Задача
Известно, что для потребительского набора
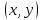 функция полезности потребителя задана уравнением
функция полезности потребителя задана уравнением 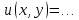 . Общий доход m, которым располагает потребитель, составляет … ден. ед. Цена товара
. Общий доход m, которым располагает потребитель, составляет … ден. ед. Цена товара  –
– 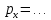 ден. ед., цена товара
ден. ед., цена товара  –
– 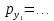 ден. ед. Предположим, что цена товара
ден. ед. Предположим, что цена товара  снижается до уровня
снижается до уровня 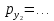 .
.Осуществите следующие действия:
- выпишите уравнение бюджетной линии и постройте график бюджетного ограничения;
- определите эффект замены (по Хиксу);
- определите эффект дохода (по Хиксу);
- определите общий эффект (по Хиксу);
- охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).
Решение
-
Бюджетное ограничение по заданным значениям и
и 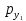 принимает вид: 4х+6у=360.
принимает вид: 4х+6у=360.
Оптимальный выбор потребителя представлен на рисунке 3.1.
Рис. 3.1. Потребительский выбор

-
Метод Хикса заключается том, что реальный доход измеряется полезностью благ, на которые расходуется денежный доход.
Исходя из условия оптимального выбора, угол наклона кривой безразличия
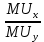 равен углу наклона бюджетного ограничения
равен углу наклона бюджетного ограничения 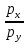 . Решаем систему уравнений:
. Решаем систему уравнений: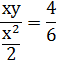
x=3y
.
Таким образом, первоначально потребитель потреблял 40 ед. товара Х и 10 ед. товара У; при этом он достигал уровня полезности U1=402*10=16 000 ютилей.
Аналогично можно рассчитать объемы товаров Х и У после изменения цены на товар У, то есть конечную оптимальную точку.
Следовательно, после снижения цены товара У, потребитель увеличил объем потребления этого товара на 6 единиц. Таким образом, общий эффект от снижения цены товара У равен +6 ед. (ΔYобщий=Yконечное – Yначальное = 16-10).
Аналогично можно рассчитать объемы товаров Х и У после изменения цены на товар У, то есть конечную оптимальную точку. X*кон.=23*2404=40 У*кон.=13*2405=16 В результате потребительский набор x,y (40; 16).
Итак, общий эффект (по Хиксу) от снижения цены составил 6 единиц (16 – 10 =6 ). Эффект замены (по Хиксу) отражает на сколько бы изменился объем потребления блага при изменении его цены в условиях сохранения потребителем прежнего (первоначального) уровня полезности.
Необходимо построить вспомогательное бюджетное ограничение U1=16 000 = x промеж.* у2промеж.
Для расчета вспомогательной точки (координаты x и y) необходимо решить систему из двух уравнений: 16000=х*у22ух=45 х=40000=34,2у=0,4*340000=13,7 График потребительского выбора представлен на рисунке 3.2.
Бланк выполнения практического задания 4
-
Технологическая норма замещения факторов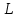 и
и 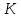 равна
равна  . Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора
. Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора 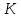 на
на  единиц. Сколько дополнительных единиц фактора
единиц. Сколько дополнительных единиц фактора 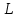 потребуется фирме?
потребуется фирме?