Файл: Планиметрия теоремаларын длелдеуді оыту дістемесіні теориялы негіздері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 205
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МАЗМҰНЫ
КІРІСПЕ…………………………………………………..............…………………3
1. ПЛАНИМЕТРИЯ ТЕОРЕМАЛАРЫН ДӘЛЕЛДЕУДІ ОҚЫТУ ӘДІСТЕМЕСІНІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ
1.1. Теорема ұғымы және оның түрлері…………………………............…………5
1.2 Математикалық теоремаларды дәлелдеу әдістері…………......................……8
2. ТЕОРЕМАЛАРДЫ ДӘЛЕЛДЕУДІҢ ӘДІСТЕМЕЛІК ЕРЕКШЕЛІКТЕРІ
2.1 Теоремаларды зерттеу және дәлелдеу әдістері...............................................12
2.2 Геометрия курсында ұғымдар мен теоремаларды енгізу әдістемесі..............17
2.3 Планиметрия курсын оқу кезінде теоремалармен жұмысты ұйымдастыру әдістемесі…………………………………………………..........................………19
ҚОРЫТЫНДЫ.......................................................................................................24
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ....................................................26
ҚОСЫМША.............................................................................................................28
КІРІСПЕ
Тақырыптың өзектілігі. Қазіргі уақытта негізгі жалпы білім беру кезеңінде оқытудың маңызды міндеті мемлекеттік білім беру стандартының нәтижелерін қамтамасыз ету болып табылады. «Математика және информатика» пәндік саласын зерттеу бірқатар міндеттерді қамтамасыз етуі керек, олардың бірі математика туралы идеяларды жалпыадамзаттық мәдениеттің бөлігі ретінде қалыптастыру, нақты процестер мен құбылыстарды сипаттауға және зерттеуге мүмкіндік беретін ғылымның әмбебап тілі.
Әрине, математика мазмұнының негізгі компоненттері ұғымдар, есептер және теоремалар болып табылады. Арифметика бойынша есептер және геометриялық нысандарға байланысты формулалар б. з. д. III мыңжылдықта жазылған мысырлық папирустарда табылған.. Алайда, бұл мәтіндерде ең бастысы — дәлелдер болған жоқ.
Біздің айналамыздағы әлемде көптеген әртүрлі заттар бар, олардың әрқайсысы белгілі бір сипаттамаларға ие: өлшемдері, пішіні, түсі, қаттылығы, химиялық құрамы және т.б. мысалы, радиусы 10 см шеңберді металл парақтан немесе қағаздан кесуге болады. Бұл заттардың бірдей сипаттамалық қасиеттері де, әртүрлі қасиеттері де болатыны түсінікті. Пішіні мен сандық сипаттамаларына келетін болсақ, олар бірдей фигуралар - радиусы 10 см болатын екі шеңбер. Материалдық әлемнің объектілері мен құбылыстарының кеңістіктік формасы мен сандық сипаттамаларын зерттейтін мектеп пәндері - алгебра және геометрия-математикаға жатады.
Геометрия-бұл нақты әлем объектілерінің кеңістіктік формасы мен сандық сипаттамалары туралы ғылым.
Басқа пәндер қоршаған орта объектілерінің басқа сипаттамаларын зерттеумен айналысады. Егер тақырыпты зерттеу барысында кеңістіктік пішін мен өлшемдерден басқа оның басқа сипаттамалары ескерілмесе, біз геометриялық фигура деп аталатын дерексіз нысанды аламыз.
«Геометрия» сөзі грек тілінен шыққан және аудармада жер өлшеуді білдіреді. Мектепте оқытылатын Геометрия ежелгі грек ғалымы Евклидтің есімімен Евклид деп аталады (б.45-тегі "геометрия шежіресінен" айдарын қараңыз). Мектеп геометриясы екі бөліктен тұрады: планиметрия және стереометрия. Планиметриямен сіз негізгі мектепте оқыдыңыз, ал стереометрияны жоғары сыныптарда оқисыз.
Математиканы оқыту әдістемесі әрдайым математиктер мен мұғалімдерді қызықтырды. Теоремаларды көрсету мәселесімен Шыныбеков А., Шыныбеков Д., Жумабаев Р және т. б. айналысты.
Теоремаларды дәлелдеуге үйрету егжей-тегжейлі қарауды қажет етеді. Оқушылар теореманы және оның дәлелдерін оның логикалық мағынасын түсінбей жай ғана жаттап алатыны белгілі.
Білімді жай ғана қайталаумен жаттау оқушының ойлау қабілетін бұзады. Егер оқушы жай материалды есте сақтаса, математикалық білім болмайды өйткені ойдың жұмысын жад жұмысымен алмастыруға болмайды.
Мұғалім бізді дұрыс түсінуі үшін математиканы оқытуда теоремалардың анықтамалары мен тұжырымдарын жаттау үлкен рөл атқаратынын атап өткіміз келеді. Бірақ мұндай жаттаудың алдында оқушыға тұжырымның әр элементін түсінуге көмектесетін жұмыс болуы керек. Оқушы кейде оны негіздеу кезінде жиі талап ететін сөздердің тіркесімін есте сақтайды, бірақ тексеру кезінде оның бұл сөздерді механикалық түрде айтқанын білуге болады. Кейде теореманы дәлелдеген оқушы дәлелдеуде айтқан элементтерін сызбада көрсете алмайды.
Зерттеу мақсаты: планиметрияны оқытуда оқушыларды теоремаларды дәлелдеуге оқытудың әдістемелік ерекшеліктерін ашу.
Зерттеу нысаны: планиметрияны оқыту процесі.
Зерттеу пәні: теоремаларды дәлелдеуді оқыту әдістемесі.
Зерттеу міндеттері:
а). «Теореманың құрылымы мен түрлері » ұғымының мәнін ашу.
ә). Теоремаларды дәлелдеудің негізгі әдістерін анықтау.
б). Теоремалармен жұмыс істеудің әртүрлі әдістерінің ерекшеліктерін ашу.
в). Планиметрия курсының кейбір теоремаларымен нұсқаулық әзірлеу.
Зерттеу құрылымы: жұмыс кіріспеден, 2 тараудан, қорытынды мен пайдаланылған әдебиеттер тізімінен тұрады.
1. ОҚУШЫЛАРДЫ ТЕОРЕМАЛАРДЫ ДӘЛЕЛДЕУГЕ ОҚЫТУ ӘДІСТЕМЕСІНІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ
1.1 Теорема ұғымы. Математикалық теоремалардың құрылымы
Планиметрия дегеніміз не?
Планиметрия - бұл геометриялық фигураларды жазықтықта зерттейтін геометрия бөлімі (сурет. 1.1).
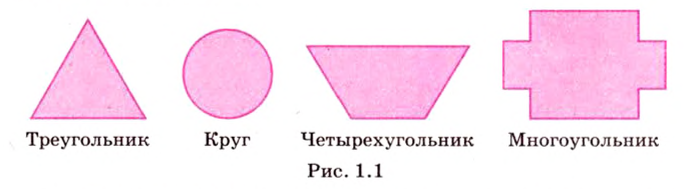
Стереометрия-бұл кеңістіктегі фигураларды зерттейтін геометрия бөлімі.
Геометриялық фигуралар-бұл айналадағы заттарға ұқсайтын дерексіз фигуралар. Бір геометриялық фигураны (немесе тұжырымдаманы) екіншісінен ажырату үшін олар анықтама деп аталатын мәлімдеме түрінде сипатталады.
Анықтама-бұл объектінің (тұжырымдаманың) оны басқалардан ажыратуға мүмкіндік беретін маңызды қасиеттерін сипаттайтын мәлімдеме. Белгілі болғандай, барлық геометриялық фигураларды анықтау мүмкін емес. Мысалы, нүкте, түзу, жазықтық. Оларды белгісіз, бастапқы (бәрі басталады) немесе планиметрияда әдеттегідей негізгі деп атайды.
Планиметрияның логикалық құрылысын келесі кезеңдердің тізбегі ретінде сипаттауға болады.
-
Негізгі деп аталатын геометриялық ұғымдарды таңдау (дерексіз фигуралар). -
Осы геометриялық тұжырымдамалардың негізгі қасиеттерін дәлелсіз шынайы деп саналатын мәлімдемелер арқылы тұжырымдау. -
Негізгі ұғымдар мен олардың қасиеттері арқылы анықталған басқа тұжырымдамалардың құрылысы және олардың ақиқаты белгілі ұғымдарға сүйене отырып, дәлелдемелер арқылы анықталған тұжырымдар.
Ғылымның бұл құрылысы аксиоматикалық деп аталады (грек. «аксиома», бұл құрмет, бедел, бұлтартпайтын шындықты білдіреді). Аксиома-бұл дәлелсіз шындық ретінде қабылданатын мәлімдеме. Дәлелдеусіз шынайы деп саналатын және басқа қасиеттерді дәлелдеуде бастапқы болып табылатын қарапайым геометриялық фигуралардың негізгі қасиеттері геометрия аксиомалары деп аталады.
Планиметрияның мектеп курсы үшін:
-
Негізгі геометриялық фигуралар (ұғымдар) - нүкте, түзу. (Нүкте-қарапайым геометриялық фигура. Барлық басқа геометриялық фигуралар нүктелерден тұрады, соның ішінде түзу.) -
Планиметрия аксиомалары-қарапайым геометриялық фигуралардың негізгі қасиеттері. -
Планиметриялық фигуралар мен олардың қасиеттерін білдіретін теоремаларды анықтау жүйесі.
Геометриядағы анықталған ұғымдарға кесінді, сәуле, үшбұрыш және т. б. жатады, өйткені олар үшін "Бұл не?». Анықталған ұғымдар көп. Мысал келтірейік.
А және В нүктелерінің арасында орналасқан А сызығының барлық нүктелерінен тұратын фигура, оның ішінде А және В нүктелері сегмент деп аталады (сурет. 1.2). А және В нүктелері сегменттің ұштары деп аталады, ал барлық басқа нүктелер сегменттің ішкі нүктелері деп аталады. Осылайша, сегмент анықталған ұғым болып табылады.
Ойлау, дәлелдемелер жүргізу, тұжырымдарды дәлелдеу дағдыларын қалыптастыру және пайдалану барлық оқу пәндерінде жүзеге асырылады. Алайда, математиканы зерттеу оқушылардың деректерді талдау, шешім қабылдау және өз таңдауын негіздеу қабілеттерін дамытуға ықпал ететіні даусыз.
А. В. Погорелов мектепте геометрияны оқытудың мақсаты былай деді: «Мектепте геометрияны оқытудың басты міндеті - оқушыларды логикалық ойлауға, өз тұжырымдарын дәлелдеуге үйрету. Мектепті бітіргендердің аз бөлігі математиктер, әсіресе геометриктер болады. Олардың практикалық қызметінде Пифагор теоремасын ешқашан пайдаланбайтындар болады.
Зерттеу жұмысын бастау үшін негізгі ұғымдарды анықтау керек – бұл аксиома және теорема.
С. И. Ожегов «пайымдау – бұл бір(тақырып) басқа (предикат) арқылы анықталатын және ашылатын ұғымдардың тіркесімін білдіретін ойлау формасы» дейді.
«Логикалық сөздік-анықтамалықтағы» пайымдауда көрсетілген объектілердің көлемі мен мазмұнына және объектілер байланысының сипатына және Н.И. Кондактардың қасиеттеріне байланысты пайымдаулардың келесі классификациясы келтірілген:
Пайымдаудың төрт негізгі түрін бөліп көрсету әдетке айналған
Қосымша 1):
Қосымша 2
Геометрияда көбінесе жалпы пайымдау немесе жалпы теріс пікірлер кездеседі. Математикада «пайымдау» терминінің орнына «бекіту» термині жиі қолданылады.
Аксиома-ғылымның бастапқы тұжырымы. дәлелдеусіз қабылданған теориялар. Мектептерде оқушылар аксиома ұғымымен танысады. Сонымен, В.А.Смирнов, Е.А. Тұяқов оқулығында «Геометрия 7 – 9» олар аксиомалар туралы былай деп жазады: «геометриялық фигуралардың қасиеттері туралы кейбір тұжырымдар бастапқы ережелер ретінде қабылданады, олардың негізінде теоремалар одан әрі дәлелденеді және тұтастай алғанда бүкіл геометрия құрылады. Мұндай бастапқы позициялар аксиомалар деп аталады».
Мектеп геометриясы үшін ең маңызды ұғым-теорема.
Теорема ұғымын бекіту ұғымы арқылы сипаттаймыз. С.И. Ожеговтың «теорема» ақиқаты дәлелдеу арқылы анықталатын мәлімдеме» деп түсініледі.
«Математика энциклопедическом сөздігінде: «Теоремасы - математикалық бекіту, оның дәлелдер арқылы белгіленген».
Логикалық анықтамалық сөздікте келесі анықтама берілген: «Теорема (грек. Theorema қарастырамын, ойланамын) аксиомаларға немесе дәлелденген ережелерге негізделген дәлелдемелердің көмегімен бекітілген ереже, мәлімдеме».
Біз құрылымды, теоремаларды қысқаша сипаттаймыз.
Теоремада нақты көрсетілуі керек: біріншіден, онда қандай да бір объект қандай жағдайда қарастырылады, екіншіден, бұл объект туралы не айтылады.
Әрбір теорема тұжырымдамалар арасындағы байланысты білдіреді. Мысалы, «үшбұрыштың бұрыштарының қосындысы 180°" теоремасында үшбұрыштың бұрыштары 180° тең» екендігі айтылған.
В. Г. Болтянскийдің пікірінше мектептегі математика курсында кездесетін теоремалардың көпшілігі келесі түрде жазылуы мүмкін:
түсіндіру бөлімінде x айнымалысы нені білдіретінін көрсету керек, содан кейін таңбамен байланысқан екі мәлімдеме жазылады.⇒. Бұл тұжырымдардың біріншісі теореманың шарты деп аталады, екіншісі теореманың тұжырымы деп аталады. Шарт және қорытынды теоремалар a(X) және B(x) предикаттарын білдіреді. Көбінесе А және В предикаттары әдетте бір айнымалыға емес, бірнеше айнымалыға байланысты болады.Егер Біз В. А. Далингердің «оқушыларды теоремаларды дәлелдеуге үйрету» оқулығына жүгінетін болсақ, онда теореманы ауызша тұжырымдау үшін 3 пікір формасы қолданылатынын көреміз:
Теореманың құрылымын талдау шартты түрде тұжырымдалған кезде тиімдірек болатыны белгілі.
Теореманың шартты формасы берілген мәлімдемені сипаттайтынын анықтауға мүмкіндік береді. Бұл үшін кішігірім ереже бар: егер объект, тұжырымдама теорема жағдайында болса, онда теорема осы тұжырымдаманың қасиетін білдіреді, егер тұжырымдама немесе объект теореманың қорытындысында болса, онда ол белгіні білдіреді.
Мысалы, теорема Пифагора: «Тікбұрышты үшбұрыштың гипотенузасының квадраты катеттің квадратына тең» .Теореманы категориялық формадан шартты формаға қайта құра отырып, бізде: « егер үшбұрыш тікбұрышты болса, онда гипотенузаның квадраты катеттің квадраттарының қосындысына тең болады». «Тікбұрышты үшбұрыш» ұғымы теорема жағдайында болғандықтан, теорема осы тұжырымдаманың қасиетін білдіреді.
Теорема: «егер екі түзу қиылысқан кезде қиылысқан бұрыштар тең болса, онда түзулер параллель болады». «Параллель түзулер» ұғымы теореманың қорытындысы, яғни бұл теореманың белгісі.