ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Уфимский государственный нефтяной технический университет»

(ИНН ФГБОУ ВО УГНТУ)

ИНН ФГБОУ ВО УГНТУ в г. Салавате
Кафедра «Оборудование предприятий нефтехимии и нефтепродукта»


Механика жидкостей и газа
Контрольная работа

ОПНН-18.03.02-02.01.081 КР 1

Исполнитель:

студент гр. БМОз-22-21 С.О.Чернихов

Руководитель:

Канд.техн.наук,доцент Р.И.Насибуллин

Салават

2023

Задача 2е.Зазор А между валом и втулкой заполнен маслом (рисунок а). Длина втулки L. К валу, диаметр которого D, приложен вращающий момент М. При вращении вала масло постепенно нагревается и скорость вращения увеличивается. Определить частоту вращения вала при температуре масла 27ºС.(Таблица 1).



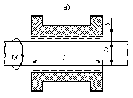
Таблица 1

M, Н·м	18,00
δ, мм	2,4
D, мм	350
l, мм	1000
жидкость	Индустриальное 30

Запишем формулу Ньютона:

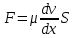(1)

где F – сила трения; – динамическая вязкость масла; S – площадь соприкосновения твердой поверхности с жидкостью; dv/dx – градиент скорости.

Площадь соприкосновения вала с жидкостью определим по формуле:

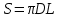(1)

Динамическую вязкость жидкости определяем по формуле:

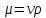(1)

где ν – кинематическая вязкость масла; ρ – плотность масла.

Поскольку толщина слоя масла мала, можно считать, что скорости в нем изменяются по прямолинейному закону.

---

Тогда формула приобретает вид:

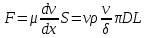(1)

Силу трения определяем из формулы момента:

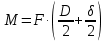(1)

Из-за малости зазора вторым членом δ/2 в скобках можно пренебречь.

При малом зазоре, когда 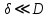, кривизной слоя жидкости пренебрегаем, рассматривая ее движение в зазоре как плоскопараллельное. Считая, что скорости v в слое масла изменяются по прямолинейному закону, эпюра касательных напряжений τ имеет вид прямоугольника. Следовательно, сила трения F проходит через центр тяжести этой эпюры, т. е. посередине слоя масла.

Частоту n вращения вала и угловую скорость ω определяем при помощи известных формул:

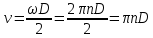(2)

Выведем формулу для определения частоты n вращения вала:

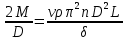(2)



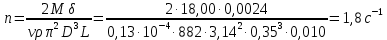
Задача 4ж.

Горизонтальный цилиндрический резервуар, закрытый полусферическими днищами, заполнен жидкостью Ж (рисунок 2).

Длина цилиндрической части резервуара L, диаметр D. Манометр показывает манометрическое давление р_М. Температура жидкости 20⁰ С. Определить силы, разрывающие резервуар по сечениям 1-1, 2-2, 3-3.(таблица 2)





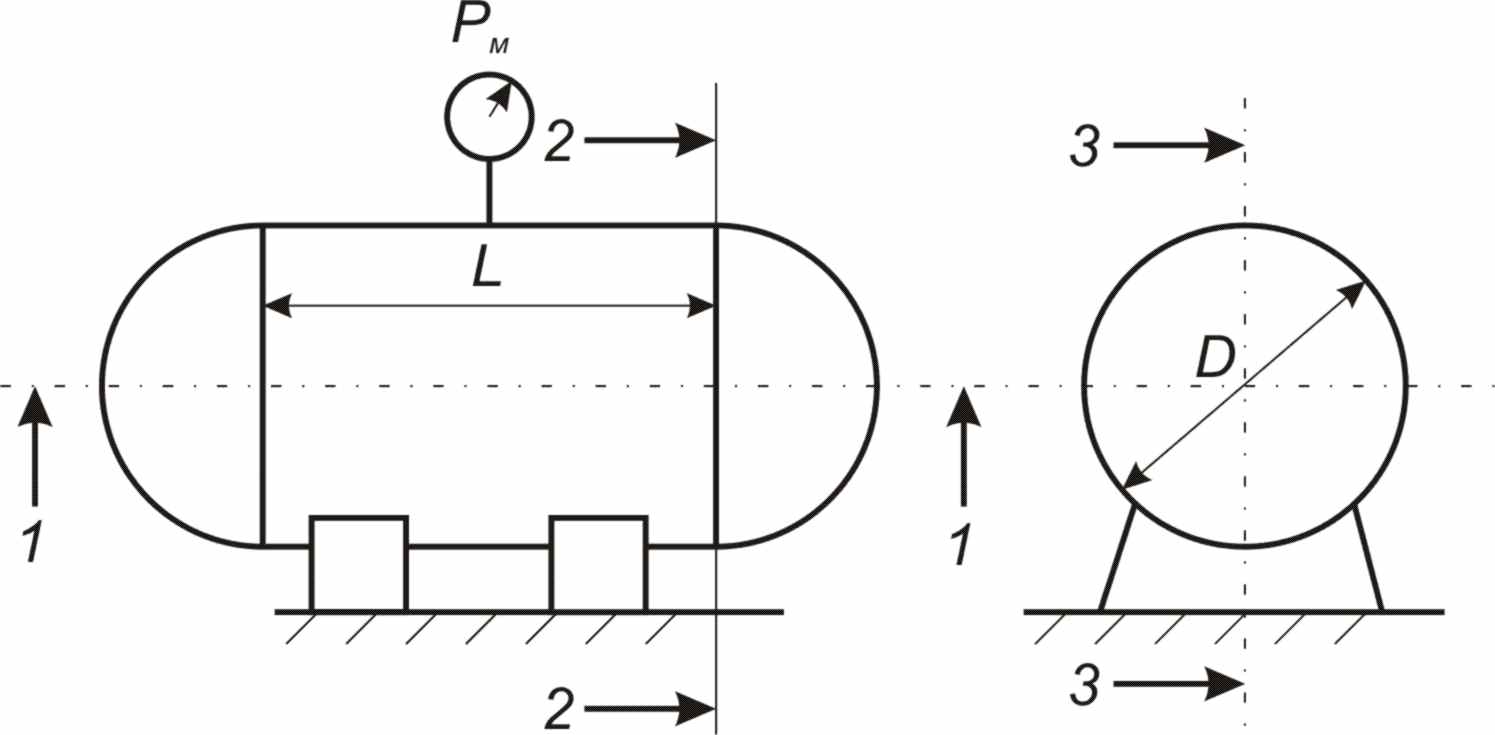
Рисунок 2

Таблица 2

Жидкость	D, м	L, м	рМ, кПа
Нефть,Баку,тяжелая	1.5	2.0	34.2

Решение:

Из основного уравнения гидростатики и учитывая вертикальную составляющую силу давления, направленную противоположно (вниз):
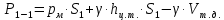(3)
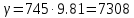– удельный вес нефти при температуре 20⁰

---

С, Н/м³;
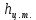– высота центра тяжести, м;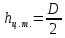
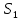- площадь сечения цистерны в сечении 1-1, м²,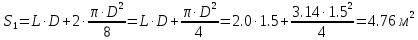


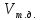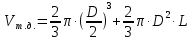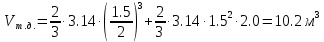
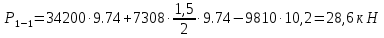
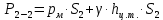- объем тела давления, м³
(3)


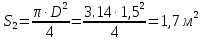
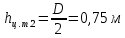
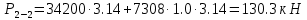
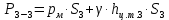(3)




(3)




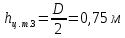
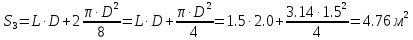
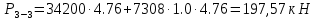
Задача 8е. Цилиндрический резервуар заполнен жидкостью Ж до высоты ¾ Н. диаметр резервуара D, температура жидкости 20⁰С (рисунок 3).
Определить:

1. 
   Объем жидкости, сливающийся из резервуара при его вращении с частотой n об/мин вокруг его вертикальной оси;
   

2. 
   Силу давления на дно резервуара и горизонтальную силу, разрывающую резервуар по сечению 1 – 1 при его вращении. (Таблица 3).
   

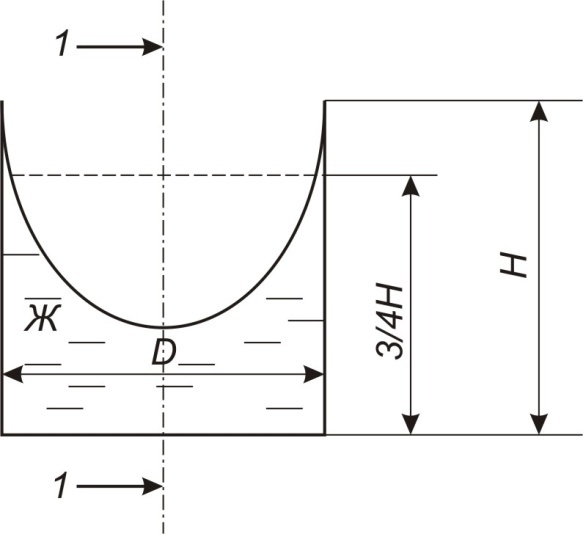
Рисунок 3

Таблица 3

Жидкость	D, м	Н, м	n, об/мин
Бензин авиационный	1.2	1. 5	76

Решение:
Определим угловую скорость:

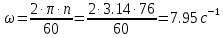
Сила давления жидкости на дно резервуара при вращении:
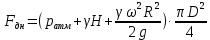(4)
р_атм – атмосферное давление, 10

---

⁵ Па;
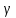- удельный вес жидкости,
– удельный вес авиационного бензина при температуре 20^о С, Н/м³;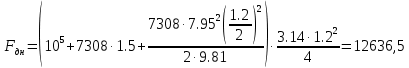

Определим объем жидкости, сливающейся из резервуара при его вращении.

Для этого необходимо найти наибольшую разницу уравнений между наименьшей точкой свободной поверхности в центре и наивысшей у боковой стенки по формуле: 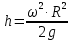- высота параболоида вращения (при вращении жидкости вместе с цилиндрическим сосудом относительно вертикальной оси симметрии с постоянной угловой скоростью, ее поверхность под действием центробежных сил вращения принимает форму параболоида вращения).
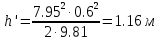(4)
Объем параболоида:
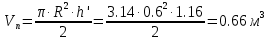(4)
Объем жидкости в резервуаре в состоянии покоя:

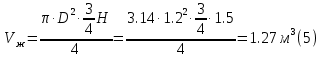
Объем резервуара:

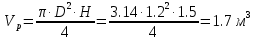(5)
Объем жидкости в резервуаре при вращении:
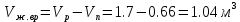(5)
Объем сливающейся жидкости в резервуаре при вращении:
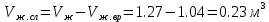(5)
Горизонтальная сила, разрывающая резервуар по сечению 1–1:
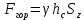(6)
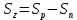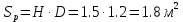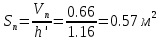- площадь вертикальной проекции жидкости, м²(4)
(4)
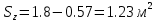(4)
(4)
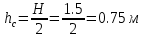- высота центра тяжести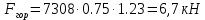.(4)
(4)

Список использованных источников

Основная литература

1) Гиргидов А.Д. Механика жидкостей и газа(гидравлика): учебник для вузов / А.Д. Гиргидов.-М.:НФРА-М,2014-704с

2) Штеренлихт Д.В. Гидравлика. В 2-х книгах – М.: Энергоатомиздат 2005.-656с.

---

Дополнительная литература

3) Шейпак А.А. Гидравлика и гидропривод. Учебник в 2ч. Ч.1:Основы механики жидкости и газа. 5-еизд.,перераб. И доп.-М.:МГИУ,2006.-266с.

4)Кудунов В.А., Карташов Э.М. Гидравлика – М.: Высшая школа,2006 – 175с.

5)Справочник по гидравлическим расчетам / Под редакций П.Г Киселева.

Изд.4-е,переработ. И доп.-М.:Энергия ,1972.-312с.

6) Большаков В.А. Справочник по гидравлике.-Киев: Вища школа,1977.-280с.

---

Смотрите также файлы

• Проектирование информационной системы формирования заказов продажи электроники.docx

• Актуальность курсовой работы.doc

• Анализ воспитательной работы за 2022 2023 учебный год класс.docx

• Методические рекомендации и практический материал к теме "Решение задач с параметрами" в контексте программы по математике для 58 классов 45.doc

• Направление подготовки 38. 03. 02 Менеджмент профиль Финансовый менеджмент.pdf