Файл: Методические рекомендации и практический материал к теме "Решение задач с параметрами" в контексте программы по математике для 58 классов 45.doc

7

6

Задачи с параметрами на уроках математики в курсе основной школы





Власова Александра Анатольевна, старший преподаватель кафедры математики, информатики и техногического образования

Барышенский Дмитрий Сергеевич, доцент кафедры математики, информатики и технологичнского образования

Краснодар, 2023




Оглавление

Введение

Мыслить человек начинает, когда у него появляется потребность что-то понять. Мышление обычно начинается с проблемы или вопроса, с удивления или недоумения, с противоречия.

Знания в значительной своей части не передаются учащимся в готовом виде, а приобретаются или в процессе самостоятельной познавательной деятельности в условиях проблемной ситуации.

Проблемное обучение заключается в создании перед учащимися проблемных ситуаций, осознании, принятии и разрешении этих ситуаций в процессе совместной деятельности учащихся и учителя при максимальной самостоятельности первых и под общим руководством последнего, направляющего деятельность учащихся.

Проблемное обучение способствует реализации двух целей:

---

1) сформировать у учащихся необходимую систему знаний, умений, навыков;

2) сформировать особый стиль умственной деятельности, исследовательскую активность и самостоятельность учащихся.

Проблемная ситуация характеризует определенное психологическое состояние учащегося, возникающее в процессе выполнения задания, для которого нет готовых средств и которое требует усвоения новых знаний о предмете, способах или условиях выполнения задания.

Для создания проблемной ситуации перед учащимися должно быть поставлено такое практическое или теоретическое задание, при выполнении которого они должны открыть подлежащие усвоению новые знания. Задание основывается на тех знаниях и умениях, которыми владеют ученики. Неизвестное, которое нужно открыть, составляет подлежащую усвоению общую закономерность, общий способ действия или некоторые общие условия выполнения действия. Следует учесть, что ни слишком трудное, ни слишком легкое задание не вызовет проблемной ситуации, поэтому предлагаемое задание должно соответствовать интеллектуальным возможностям учащихся.

Принято различать четыре основных звена процесса проблемного обучения:

- осознание общей проблемной ситуации;

- анализ ее, формулировка конкретной проблемы;

- решение проблемы (выдвижение, обоснование гипотез, последовательная проверка их);

- проверка правильности решения проблемы.

Безусловно, проблемный метод нельзя превращать в универсальный метод обучения. Для некоторых учащихся он несколько труден. Да и времени он требует больше, чем традиционное информационно-сообщающее изложение. Поэтому проблемный метод следует использовать дозированно, если уверены в успехе его применения.

Технология обучения решению задач с параметрами

Известно, что в программах по математике задачам с параметрами отводится незначительное место. Поэтому, в первую очередь, укажем разделы общеобразовательной математики, в которых вообще присутствует сама идея параметра:

Функция прямая пропорциональность: y=kx

(x, y-переменные, k-параметр, k  0)

Линейная функция: y=kx+b

(x и y-переменные, k и b-параметры)

Линейное уравнение: ax+b=0

(x-

---

переменная, a и b-параметры)

Уравнение первой степени: ax+b=0

(x-переменная, a и b-параметры, a  0)

Линейное неравенство

Квадратное уравнение: ax²+bx+c=0

(x-переменная, a, b, c-параметры, a  0)

Квадратичная функция: y=ax²+bx+c

(x и y-переменные, a, b, c-параметры)

Квадратные неравенства

В содержание каждой названной темы включается блок материала, связанный с параметром.

При методической разработке этого блока выделяются следующие шаги:

1) Изучение программы и учет "требований жизни".

2) Анализ учебного материала.

3) Методы решения и составления задач по теме.

4) Выбор алгоритмов решения типовых задач.

В первую очередь следует определить вопросы теории, знания и умения, которые должны быть сформированы у всех учеников; число часов, отводимое на изучение темы.

Успех работы над темой во многом зависит от того, как удается учесть "требования жизни". В любом классе имеется значительное число учащихся, которые готовятся поступать в высшие учебные заведения, где требуется серьезная математическая подготовка.

При отборе материала учитывается подготовка учащихся класса, результаты работы по предыдущим темам. На основе этого учитель определяет материал для повторения.

Затем необходимо уточнить затраты времени на изучение темы в целом и по отдельным урокам, определить содержание материала предстоящей лекции.

Весь материал рассортировывается. Главная часть-тот материал, который будет изучаться на уроках, далее-материал для занятий факультатива, индивидуальных заданий, специальный материал для работы со старшеклассниками.

Под "главным содержанием" понимается та часть материала, без усвоения которой не могут быть решены задачи изучения темы.

Определив главное, надо выбрать психологически правильную линию поведения, которая заставит ребят самостоятельно определить метод решения, установить особенности задачи, систематизировать материал.

Далее можно приступить к прогнозированию затруднений учащихся и возможных типичных ошибок.

---

Для выявления затруднений учащихся желательно изучить требования к учащимся к овладению общеучебными умениями. Это позволяет:

а) выявить навыки учебного труда, которые не сформированы у учащихся, но им необходимы;

б) установить, какие из общеучебных умений можно продолжить формировать при работе над темой;

в) определить наличие в системе упражнений задания для формирования общеучебных умений;

г) спрогнозировать возможность самостоятельного изучения отдельных частей материала.

На следующем шаге методической разработки важно повторить и систематизировать методы решения задач по этой теме. Для этого требуется:

а) выделить типы задач;

б) определить методы решения этих задач;

в) продумать методику знакомства учащихся с избранными методами решения.

При решении задач с параметрами преимущественно применяются два метода: графический и аналитический.

При выделении методов решения задач по теме следует помнить, что сложная задача чаще всего имеет единственный метод решения.

Важна работа и по составлению задач. Методы составления задач могут быть такими:

1. Конструкция примера сохраняется, но вносятся изменения в числовые данные или в требование задачи, либо одновременно.

Пример: 1) Исходное задание.

При каких значениях параметра aуравнение имеет четыре различных решения?

,

.

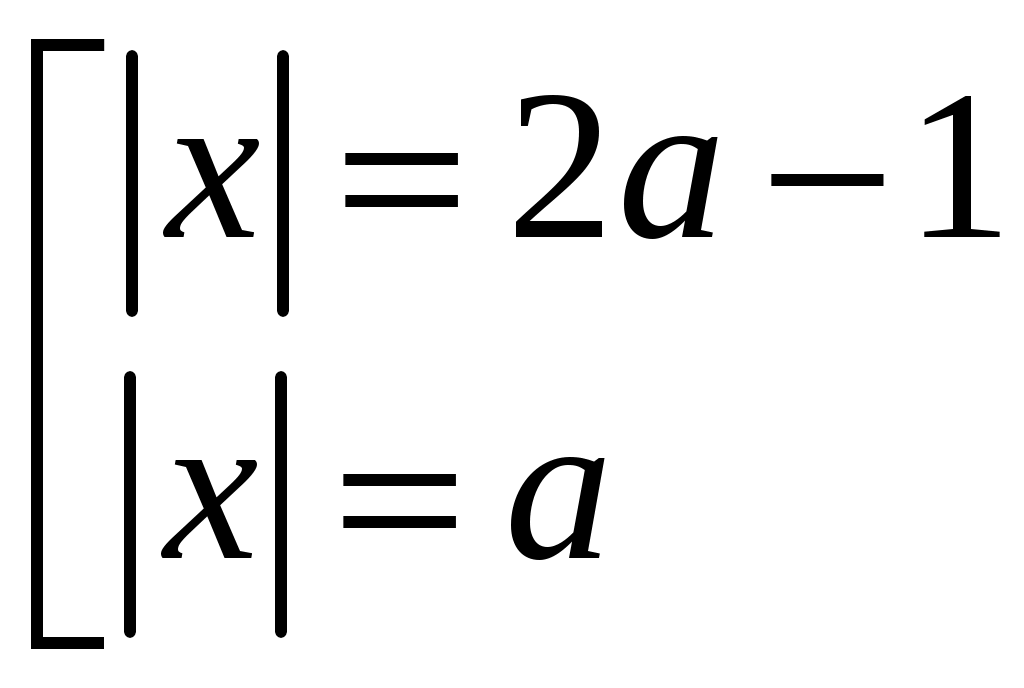Для того чтобы исходное уравнение имело четыре решения, необходимо, чтобы каждое уравнение совокупности имело два различных решения, и они не совпадали.



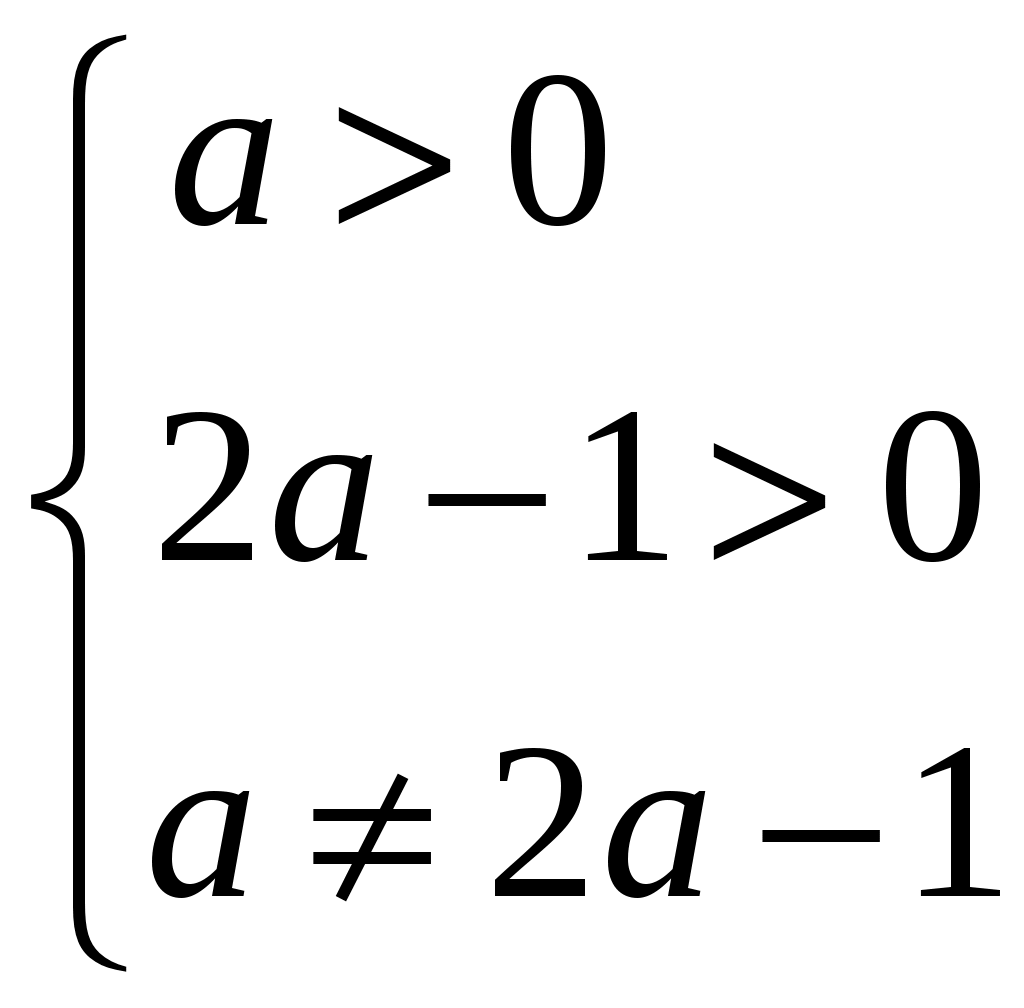
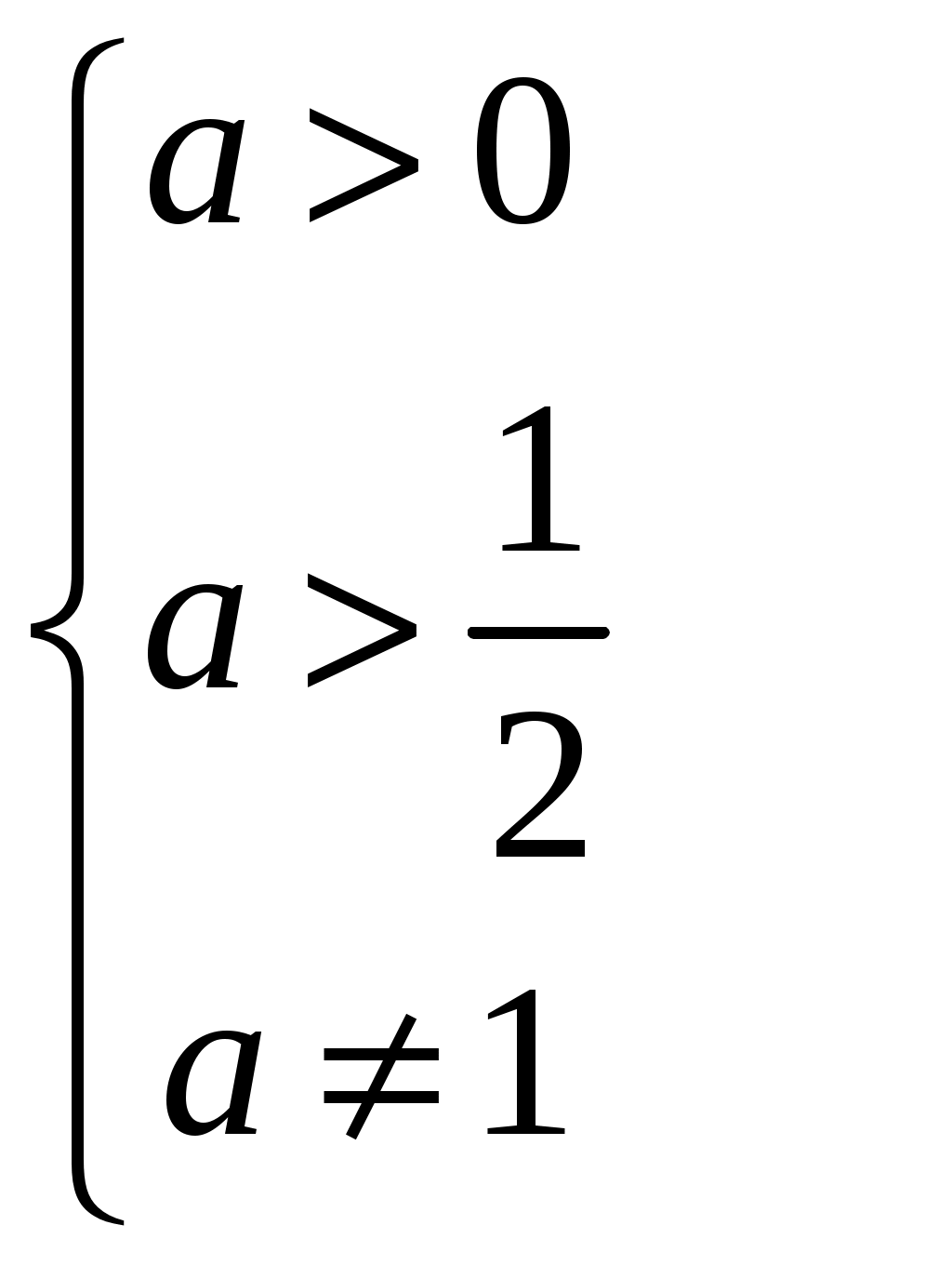
Ответ: .

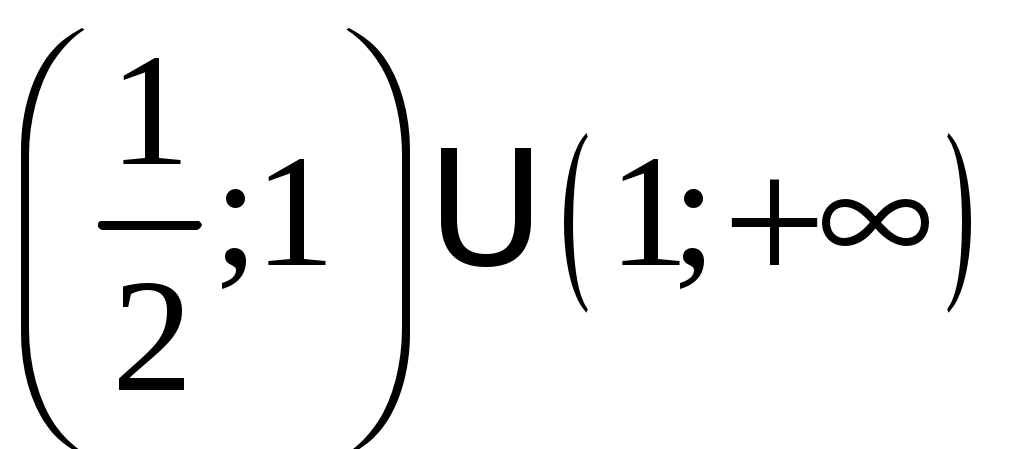2) Изменим задание.

При каких значениях параметра b уравнение

имеет два различных решения?

---

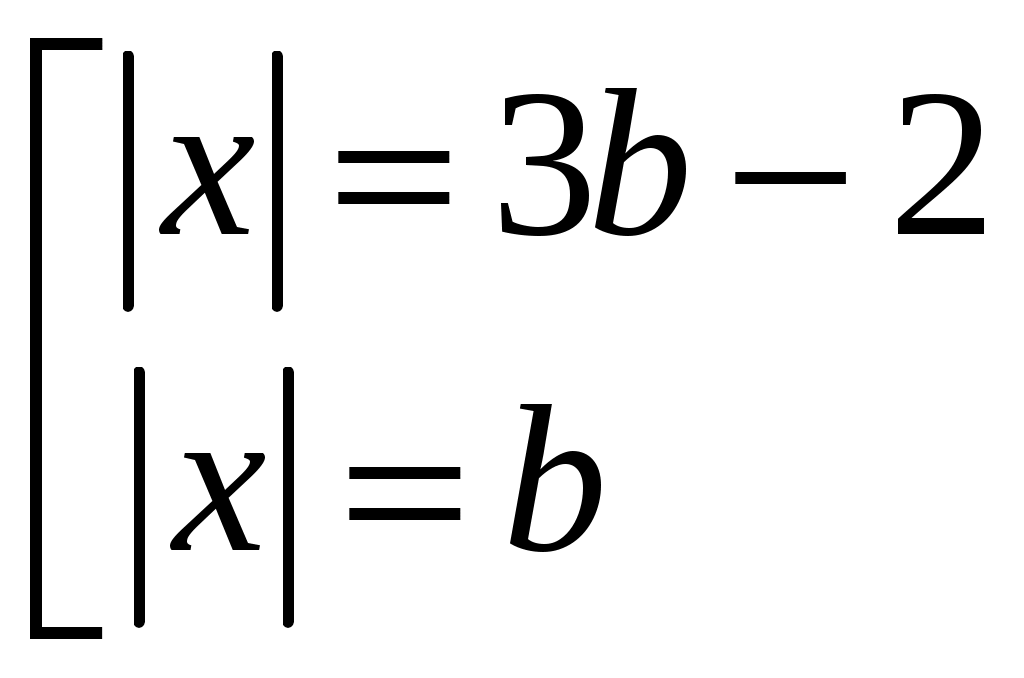
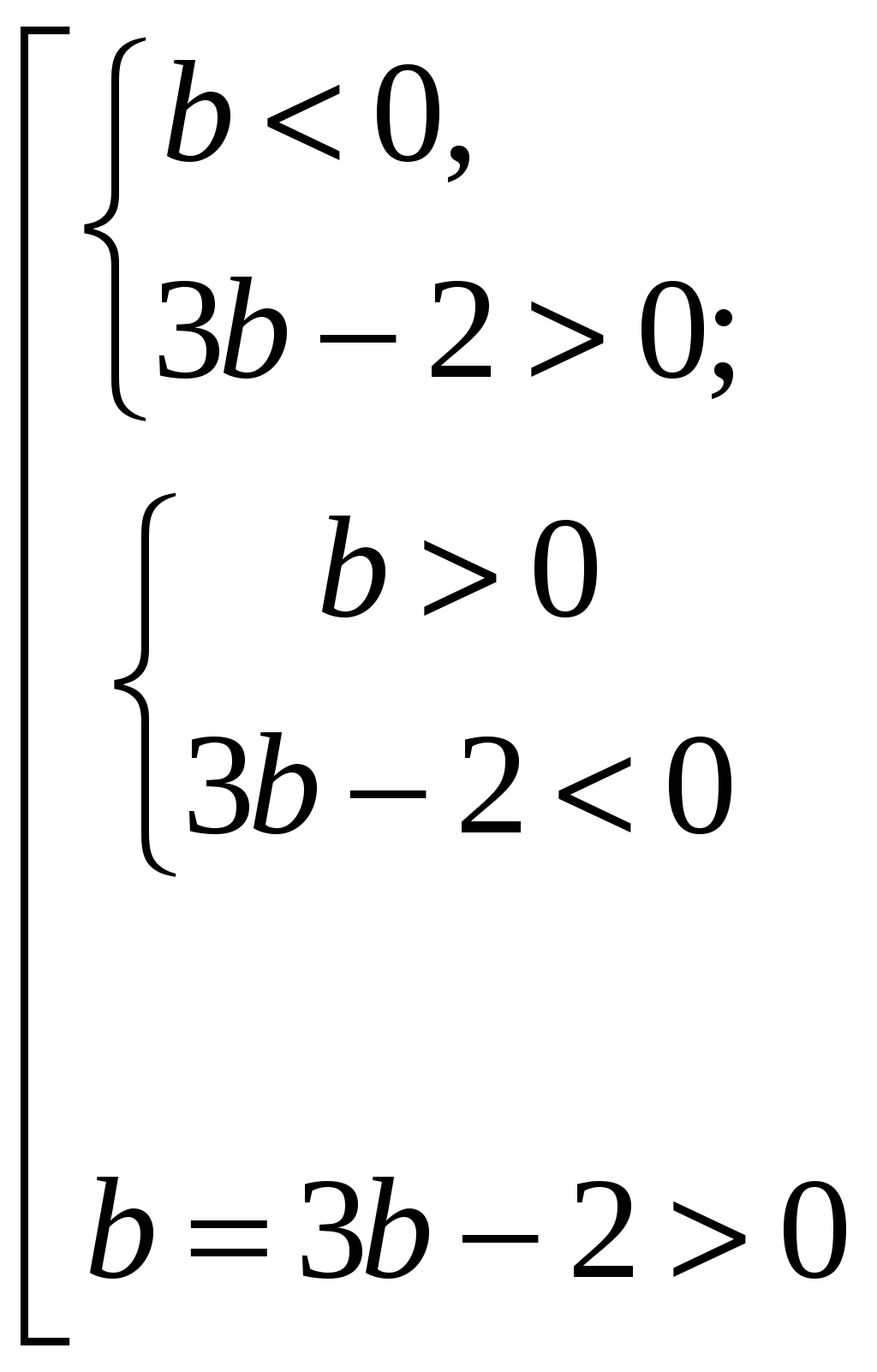
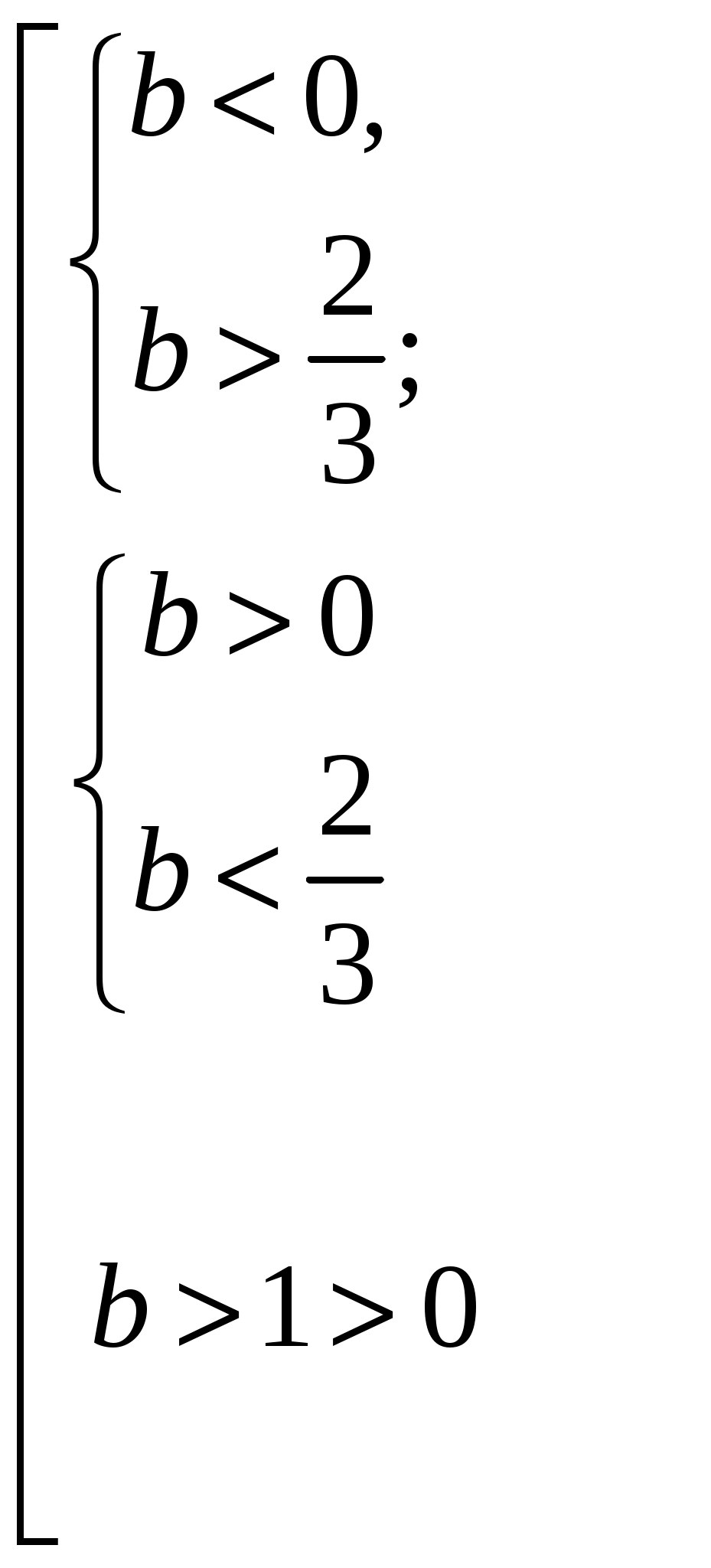
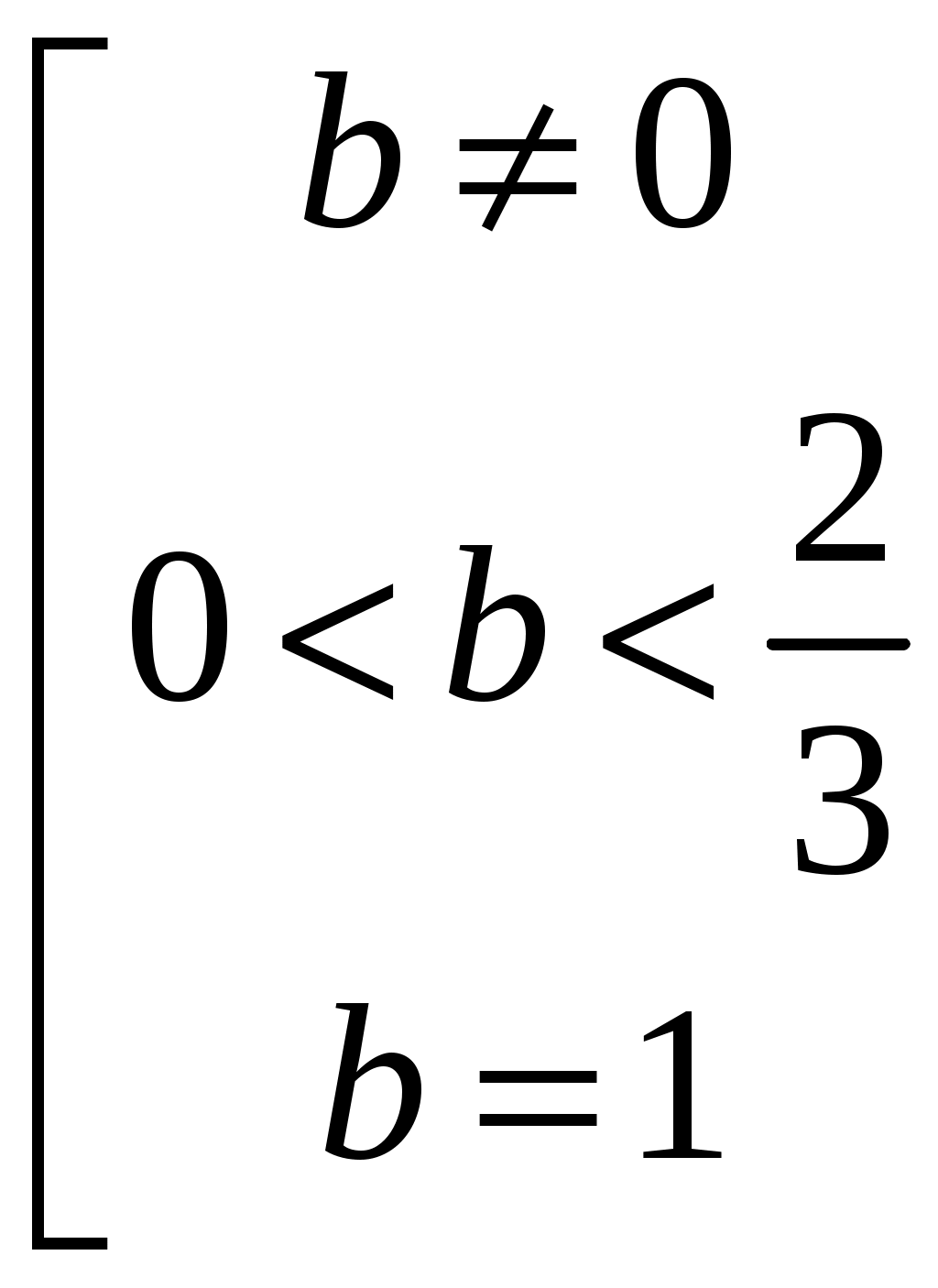
Ответ: .

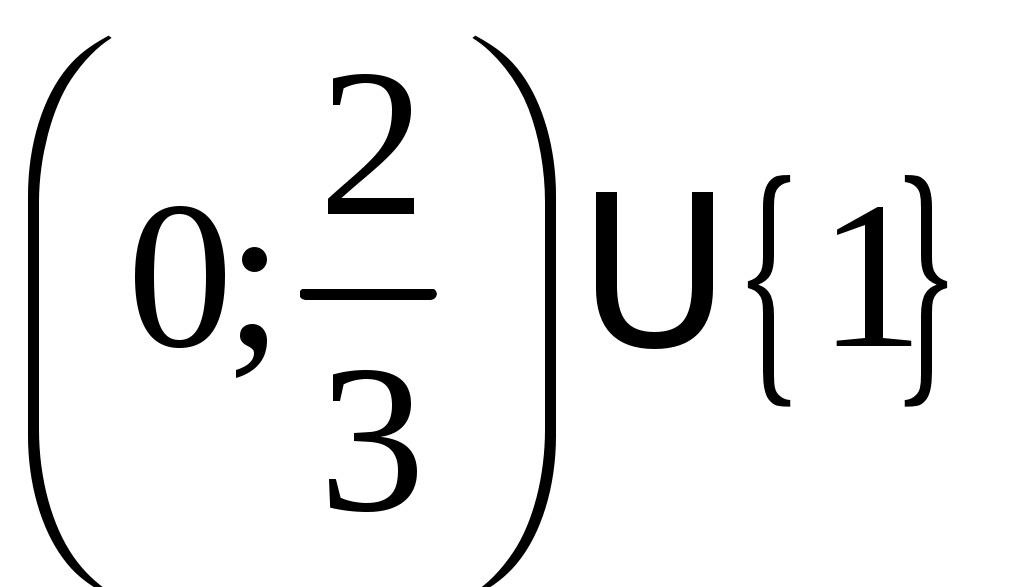2. В известных примерах числовые данные заменяются параметрами.

Пример: В исходном примере: решить уравнение -выделяется число 2, которое может быть заменено параметром. Получим: . Решение последнего уравнения содержит элементы исследования, так как нужно учесть условие , вспомнив определение целой части.

3. Составление уравнения, решаемого тем же приемом, что и исходное:

Пример: Исходное уравнение: (1)

1) Рассмотрим данное уравнение как квадратное относительно a.

;

;

;





(2) Таким образом, уравнение (1) распадается на два квадратных уравнения относительно x:





Ответ:

при корней нет;

при

---