1. 
   Уравнение, характеризующее полное число столкновений разных молекул в единице объёма за единицу времени
   

2. 
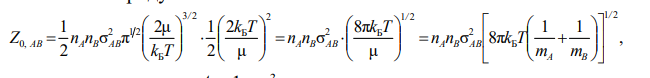
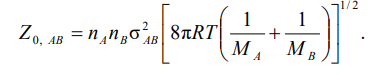
   Уравнение, характеризующее полное число столкновений одинаковых молекул в единице объёма за единицу времени
   

3. 
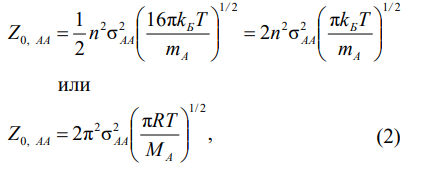
   Полное число столкновений измеряется в 1/(см3 ꞏс)
   
4. 
   Частота столкновений – характеризует полное число столкновений молекул А за единицу времени при условии, что их количество в 1 см3 равно единице; Если количество частиц А и В в 1 см3 равно единице, то полное число столкновений молекул А и В
   
5. 
   Уравнение частоты столкновений разных частиц
   

6. 
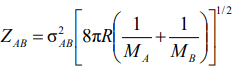
   Уравнение частоты столкновений одинаковых частиц
   

7. 
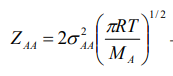
   Частота столкновений одинаковых частиц обозначается буквой
   
8. 
   
   
9. 
   Частота столкновений измеряется в см3 /с
   
10. 
    Эффективный диаметр столкновений – это минимальное расстояние, на которое сближаются центры двух молекул при столкновении. При столкновении, молекулы сближаются до некоторого наименьшего расстояния, которое условно считается суммой радиусов взаимодействующих молекул.
    
11. 
    Диаметр столкновений равен
    

12. 
    Уравнение эффективного диаметра столкновений
    

13. 
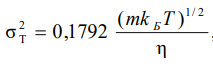
    Зависимость эффективного диаметра столкновений от температуры описывается уравнением
    

14. 
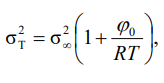
    Формулировка гипотезы активных столкновений
    

к реакции приводят только те столкновения

---

, энергия которых превышает некоторую критическую величину – энергию активации Е. Такие столкновения являются активными

15. 
    Активные столкновения – это это столкновения, энергия которых превышает некоторую критическую величину – энергию активации Е
    
16. 
    Число активных столкновений зависит от следующих факторов: энергетического и стерического
    
17. 
    Уравнение гипотезы активных столкновений
    

18. 
    Стерический множитель показывает вероятность соответствующей геометрической конфигурации при столкновении
    
19. 
    Значение стерического множителя изменяется в интервале от 10^{– 5} до 1
    
20. 
    Доля активных столкновений равна
    

21. 
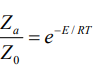
    Теория активных столкновений основывается на том, что химическое взаимодействие осуществляется только при столкновении активных частиц, которые обладают достаточной энергией для преодоления потенциального барьера реакции и ориентированы в пространстве друг относительно друга.
    

22. 
    По теории активных столкновений скорость химической реакции пропорциональна числу столкновений между частицами в единице объема в единицу времени
    
23. 
    Уравнение теории активных столкновений для скорости бимолекулярных реакций
    

24. 
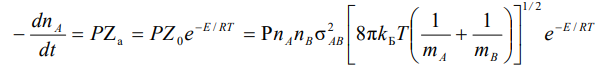
    Уравнение теории активных столкновений для константы скорости бимолекулярных реакций
    

25. 
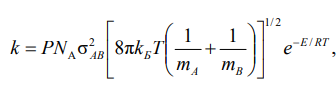
    Уравнение теории активных столкновений для истинной энергии активации бимолекулярной реакции
    

26. 
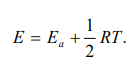
    Поверхность потенциальной энергии реакции – это взаимодействия атома С с двухатомной молекулой АВ
    
27. 
    Активированный комплекс (переходное состояние) реакции двухатомной молекулы АВ и атома С – это это состояние, когда молекулы АВ и ВС отдельно не существуют, а атом В в одинаковой степени принадлежит молекулам АВ и ВС
    
28. 
    Координата (путь) реакции – это наиболее энергетически выгодный (с минимальной энергией) маршрут реакции
    
29. 
    Профиль пути реакции – это зависимость потенциальной энергии от координаты реакции
    
30. 
    Теория активированного комплекса основывается на том, что элементарный акт взаимодействия молекул состоит в постепенной перестройке химических связей, при котором начальная конфигурация атомов в исходных молекулах переходит в конечную у продуктов реакции при непрерывном изменении межатомных расстояний.
    
31. 
    Изоэнергетические линии поверхности потенциальной энергии реакции – это линии, вдоль которых потенциальная энергия одинакова
    
32. 
    По теории активированного комплекса скорость химической реакции пропорциональна концентрация активных комплексов, пересекающих потенциальный барьер вдоль координаты реакции, за единицу времени в единице объема
    
33. 
    Уравнение теории активированного комплекса для скорости бимолекулярных реакций
    

---

34. 
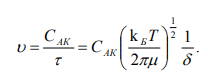
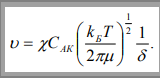
    Трансмиссионный коэффициент показывает равный доле активных комплексов, которые преодолевают энергетический барьер и распадаются при этом на конечные продукты реакции
    
35. 
    Три предположения, лежащие в основе метода переходного состояния для расчета константы скорости реакции
    

36. 
    Для адиабатических процессов трансмиссионный коэффициент равен 1
    
37. 
    К свободной энергии активации можно отнести
    

38. 
    Свободная энергия активации – это это величины, характеризующие изменение свободной энергии системы при ее переходе из исходного в переходное состояние с учетом всех степеней свободы, кроме поступательного движения вдоль координаты реакции.
    
39. 
    Уравнение теории активированного комплекса для константы скорости бимолекулярных реакций
    

40. 
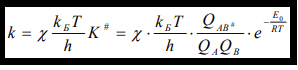
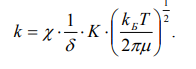
    Уравнение теории активированного комплекса для константы скорости бимолекулярной реакции при Р = const
    

41. 
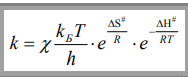
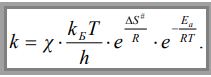
    Уравнение теории активированного комплекса для энтальпии активации бимолекулярной реакции
    

42. 
    Уравнение теории активированного комплекса для свободной энергии Гиббса активации бимолекулярной реакции
    

43. 
    Уравнение Эйринга для константы скорости бимолекулярной реакции
    

---

44. 
    Уравнение теории активированного комплекса для константы равновесия между реагентами и активированным комплексом
    

45. 
    При взаимодействии двух атомов теории активных столкновений и активированного комплекса дают кинетические результаты, которые одинаковые
    
46. 
    При взаимодействии двух нелинейных многоатомных молекул теории активных столкновений и активированного комплекса дают кинетические результаты, которые отличающиеся
    
47. 
    Основное положение теории Линдемана
    

• 
  активация для мономолекулярных реакций является результатом соударений, то есть бимолекулярным процессом. Скорость реакции пропорциональна не числу столкновений, а доле А* активных молекул. При этом выполняется кинетический закон I порядка.
  
• 
  при высоких давлениях усиливаются столкновения, большинство активных молекул дезактивируются, при этом выполняется кинетическое уравнение I порядка. При понижении давления время столкновения возрастает до величины, большей, чем время жизни А*, большинство активных молекул распадаются на продукты и реакция переходит в реакцию II порядка.
  

48. 
    Теория Линдемана основана на теории ТАС
    
49. 
    Теория Линдемана была предложена для реакций мономолекулярных реакций
    
50. 
    Укажите последовательность стадий в кинетической схеме Линдемана Активация частицы А, Дезактивация частицы A^*, Собственно химическая реакиця мономолекулярного распада частицы A^*
    
51. 
    При высоких давлениях мономолекулярная реакция распада подчиняется кинетическому уравнению 1-го порядка
    
52. 
    Уравнение скорости мономолекулярной реакции распада частицы А при высоких давлениях
    

53. 
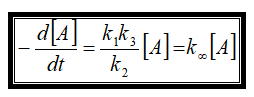
    При низких давлениях мономолекулярная реакция распада подчиняется кинетическому уравнению 2-го порядка
    
54. 
    Уравнение скорости мономолекулярной реакции распада частицы А при низких давлениях
    

---

55. 
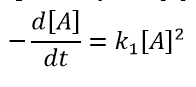
    При понижении давления порядок мономолекулярной реакции распада частицы А меняется с 1 на 2
    
56. 
    Виды тримолекулярных реакций валентно ненасыщенные и насыщенные
    
57. 
    Роль третьей частицы в тримолекулярной реакции с участием атомов и радикалов заключается отвода избыточной энергии от образовавшейся молекулы
    
58. 
    Уравнения тримолекулярных реакций в газовой фазе с участием оксида азота (II)
    

59. 
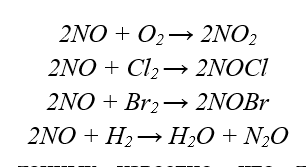
    Для тримолекулярных реакций в газовой фазе с участием оксида азота (II) с ростом температуры скорость химической реакции падает
    
60. 
    С ростом температуры скорость реакции образования хлористого нитрозила снижается, поскольку уменьшения концентрации NOCl₂
    
61. 
    По теории активированного комплекса константы скоростей мономолекулярных реакции в газовой фазе и растворе отличаются
    

---

Смотрите также файлы

• Stud kz аза тілінде жазылан жмыстар саны жне сапасы бойынша бізді ор 1 болып табылады.docx

• Гигиенические требования к микроклимату производственных помещений.docx

• Учебная программа по учебному предмету Русский язык для 1011 классов общественногуманитарного направления уровня общего среднего образования по обновленному содержанию.pdf

• И. И. Иванов инициалы и фамилия Руководитель ст преподаватель.pdf

• Курсовая работа направления и пути совершенствования процесса транспортировки материальнотехнических ресурсов по мдк 02. 03 Оптимизация процессов транспортировки и проведение оценки стоимости затрат на хранение товарных запасов.docx