Файл: Методические указания по выполнению курсовой работы для студентов 1 курса всех форм обучения.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Метод итераций основан на последовательном задании аргумента x и вычислении по нему функции F1(x), причем очередное значение x приращивается предыдущему значению функции x(n+1)=F1(x(n)) до тех пор, пока соблюдается условие |x(n+1)-x(n)|>=E. Первоначальное значение аргумента x (первое приближение – x(1)) определяется из таблицы как ближайшее к месту перехода функции F(x) через нуль. Последнее приближение x и будет корнем уравнения с точностью E [8].
Метод половинного деления (дихотомии) состоит в следующем.
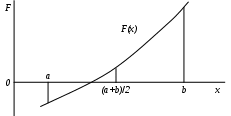
Рис.4. Геометрическое представление метода половинного деления
Метод Ньютона (касательных) основан также на последовательном задании значений x и вычислении функции F(x), причем очередное значение x определяется формулой:
x(n+1)=x(n)-F(x(n))/F’(x(n)),
где F’(x(n)) – производная от функции F(x) в точке x(n).
Геометрически производная от F(x), как известно, по величине равна тангенсу угла наклона касательной к кривой F(x) в точке x. Тогда точка x(n+1) есть точка пересечения с осью абсцисс касательной к кривой F(x), проведенной в точке x=x
(n). См. рис. 5.
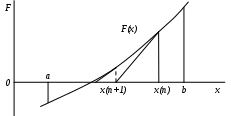
Рис. 5. Геометрическое представление метода Ньютона
Как и в методе итераций, начальное значение x задается как ближайшее табличное к месту перехода функции F(x) через нуль.
Выражение для производной F’(x) получают аналитически в результате дифференцирования функции F(x). Значение производной может быть получено приближенно и численным методом:
F’(x)=(F(x+E)-F(x))/E.
Итерационный процесс приближения к корню (последовательное вычисление x(n+1)) продолжается до тех пор, пока будет выполняться условие |x(n+1)-x(n)|>=E.
Следует иметь в виду, что при выполнении задания и алгоритм, и программа должны предусматривать оба этапа работы: табулирование функции F(x) с выбором начального приближения и процесс поиска корней с заданной точностью.
4. ТРЕБОВАНИЯ К ПОЯСНИТЕЛЬНОЙ ЗАПИСКЕ КУРСОВОЙ РАБОТЫ
Отчет по курсовой работе должен включать в себя:
1). Титульный лист.
2). Оглавление.
3). Введение.
4). Решения задач 1, 2, 3, 4.
5). Заключение.
Форма и содержание титульного листа пояснительной записки представлены на рис. 6.
Федеральное агентство по образованию
ГОУ ВПО «Уральский государственный технический университет – УПИ»
Кафедра прикладной геометрии и
информатики
К У Р С О В А Я Р А Б О Т А
по информатике
Работа защищена с оценкой
подпись дата
Екатеринбург
2003
Рис.6. Образец титульного листа отчета по курсовой работе
Оглавление пояснительной записки должно включать в себя заголовки всех разделов с указанием страниц.
Введение должно быть кратким (не более 0.5 стр.) и содержать информацию о содержании выполненной работы.
Решение каждой задачи
должно включать:
В заключении очень кратко (в двух – трех предложениях) изложить результаты работы.
0>
Метод половинного деления (дихотомии) состоит в следующем.
-
Определяем начальное значение x=(a+b)/2 (как результат деления интервала [a,b] пополам). -
Вычисляем F(x). -
Если F(x)>0 и F(a)>0 или F(x)<0 и F(a)<0 (т.е. перемена знака функции F(x) не произошла), то задаем a=x (т.е. перемещаем левую границу интервала в середину), уменьшая интервал вдвое и исключая при этом левую половину, на которой либо нет корней, либо есть четное число корней, иначе задаем b=x (исключаем правую половину интервала). См. рис. 4. -
Проверяем условие b-a<E, если оно выполняется, то возвращаемся к п.1. с новыми значениями границ интервала, иначе заканчиваем вычисления и считаем, что последнее значение xи будет корнем уравнения с заданной точностью E.

Рис.4. Геометрическое представление метода половинного деления
Метод Ньютона (касательных) основан также на последовательном задании значений x и вычислении функции F(x), причем очередное значение x определяется формулой:
x(n+1)=x(n)-F(x(n))/F’(x(n)),
где F’(x(n)) – производная от функции F(x) в точке x(n).
Геометрически производная от F(x), как известно, по величине равна тангенсу угла наклона касательной к кривой F(x) в точке x. Тогда точка x(n+1) есть точка пересечения с осью абсцисс касательной к кривой F(x), проведенной в точке x=x
(n). См. рис. 5.

Рис. 5. Геометрическое представление метода Ньютона
Как и в методе итераций, начальное значение x задается как ближайшее табличное к месту перехода функции F(x) через нуль.
Выражение для производной F’(x) получают аналитически в результате дифференцирования функции F(x). Значение производной может быть получено приближенно и численным методом:
F’(x)=(F(x+E)-F(x))/E.
Итерационный процесс приближения к корню (последовательное вычисление x(n+1)) продолжается до тех пор, пока будет выполняться условие |x(n+1)-x(n)|>=E.
Следует иметь в виду, что при выполнении задания и алгоритм, и программа должны предусматривать оба этапа работы: табулирование функции F(x) с выбором начального приближения и процесс поиска корней с заданной точностью.
4. ТРЕБОВАНИЯ К ПОЯСНИТЕЛЬНОЙ ЗАПИСКЕ КУРСОВОЙ РАБОТЫ
-
СОСТАВ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ
Отчет по курсовой работе должен включать в себя:
1). Титульный лист.
2). Оглавление.
3). Введение.
4). Решения задач 1, 2, 3, 4.
5). Заключение.
-
СОДЕРЖАНИЕ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ
Форма и содержание титульного листа пояснительной записки представлены на рис. 6.
Федеральное агентство по образованию
ГОУ ВПО «Уральский государственный технический университет – УПИ»
Кафедра прикладной геометрии и
информатики
К У Р С О В А Я Р А Б О Т А
по информатике
-
Выполнил
Студент:
Группа:
Иванов И.И.
М-XXXХХ
Принял
Петров П.П.
Работа защищена с оценкой
подпись дата
Екатеринбург
2003
Рис.6. Образец титульного листа отчета по курсовой работе
Оглавление пояснительной записки должно включать в себя заголовки всех разделов с указанием страниц.
Введение должно быть кратким (не более 0.5 стр.) и содержать информацию о содержании выполненной работы.
Решение каждой задачи
должно включать:
-
постановку задачи (что дано и что требуется выполнить); -
исходные выражения и исходные данные принятого варианта; -
таблицу принятых обозначений переменных, которые присутствуют в формулах и используются в программах; -
алгоритм решения задачи; -
по возможности краткие пояснения к алгоритмам с указанием особенностей ввода данных и вывода результатов; -
результаты решения задачи в виде таблиц, графиков; -
краткий анализ результата (с указанием степени влияния того или иного переменного параметра).
В заключении очень кратко (в двух – трех предложениях) изложить результаты работы.