Файл: Методические указания по выполнению курсовой работы для студентов 1 курса всех форм обучения.doc

2.4. ЗАДАЧА 4. ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ С ЗАДАННОЙ ТОЧНОСТЬЮ

По заданному нелинейному уравнению

F(x)=0,

где F(x) – некоторое нелинейное аналитическое выражение, определенное на интервале

[a, b],

вычислить корни этого уравнения с требуемой точностью E одним из трех методов:

1. 
   итераций;
   
2. 
   половинного деления;
   
3. 
   Ньютона.
   

Исходные данные для решения нелинейных уравнений приведены в табл. 4.

Таблица 4

---

Исходные данные для решения нелинейных уравнений

Вариант	Выражение	Интервал		Метод	Точность
№	F(x)	a	b	N	E
00		2	3	1	10-5
01		0	2	3	10-5
02		0	1	2	10-5
03		0,4	0,85	1	10-6
04		0,1	2	2	10-5
05		1	0,8	2	10-5
06		0	1	1	10-6
07		0,1	4	3	10-5
08		2	2	2	10-5
09		1	1	1	10-5
10		0	1	3	10-6
11		0,1	3	2	10-5
12		1	2	1	10-5
13		1,2	6	3	10-6
14		-1,5	-0,3	2	10-6
15		1	2	3	10-5
16		1	3	2	10-5
17		3	5	2	10-6
18		0,5	2	3	10-5
19		0	1,5	1	10-5
20		0	1	2	10-6
21		1	3	3	10-6
22		1	2	1	10-5
23		1,5	2,5	2	10-5
24		-2	0	3	10-6
25		3	4	2	10-6
26		2	5	3	10-6
27		0	2	2	10-5
28		0,5	1,5	1	10-5
29		1	3	3	10-6
30		1	2	2	10-6

---

3. РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ РАБОТЫ

Курсовая работа оформляется как единая программа. При этом целесообразным представляется применение принципа модульного программирования, согласно которому программа каждой задачи оформляется как отдельный модуль. Объединение всех модулей в единую программу можно выполнить с помощью отдельного управляющего модуля, в котором предусматривается в диалоговом режиме вывод наименования работы, выбор решения той или иной задачи и завершение работы по соответствующей команде, вводимой с клавиатуры.
3.1. РЕШЕНИЕ ЗАДАЧИ 1

При разработке модуля программы расчета трансформатора можно рекомендовать:

1. 
   Ввод исходных данных U, S, n, m производить программно (указать значения этих величин непосредственно в тексте программы), а данные о U_i, I_i – с клавиатуры в диалоговом режиме с соответствующими подсказками.
   
2. 
   В вывод результатов расчетов наряду с получаемыми величинами количества витков и диаметра провода всех обмоток поместить и все исходные данные, соответствующим образом их упорядочив и сопроводив текстом.
   

3.2. РЕШЕНИЕ ЗАДАЧИ 2

При разработке модуля программы расчета амплитудно-частотной характеристики можно рекомендовать:

1. 
   Ввод всех исходных данных осуществить программно (указать значения величин непосредственно в тексте программы).
   
2. 
   Таблицу значений амплитудно-частотной характеристики A(W) при различных Z целесообразно представить либо как три одномерных массива, либо как один двумерный массив размерности 11х3.
   
3. 
   Для получения таблицы значений амплитуды A(W) при различных значениях Z применить вложенный цикл (внешний – по Z, внутренний – по W).
   
4. 
   Построение графика амплитудно-частотной характеристики нужно выполнить по точкам, соответствующим табличным значениям.
   
5. 
   При формировании выходных данных целесообразным представляется также вывод на экран всех исходных данных с соответствующими текстовыми сопровождениями.
   

3.3. РЕШЕНИЕ ЗАДАЧИ 3

При разработке модуля программы численного интегрирования функции необходимо иметь в виду следующее.

Вычисление определенного интеграла от функции f(x) с пределами интегрирования a и b, как известно, равносильно определению площади фигуры, ограниченной ординатами

---

а и b, осью абсцисс и графиком подынтегральной функции f(x). См. рис. 1.



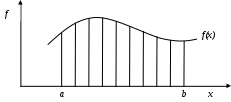
Рис.1. Графическое представление численного интегрирования

При численном интегрировании отрезок [a,b] разбивается на n интервалов длиной

h=(b-a)/n, и тогда искомая площадь представляется суммой площадей n элементарных фигур.

В зависимости от того, каким образом определяется площадь элементарной фигуры S, получает название метод численного интегрирования. См. рис. 2.

Если площадь элементарной фигуры определяется приближенно как площадь прямоугольника – получаем метод прямоугольников (рис. 2-1).

Если площадь элементарной фигуры представляется площадью соответствующей трапеции – получаем метод трапеций (рис. 2-2).

Если элементарная фигура заменяется фигурой, в которой функция f(x) представляется параболой – получаем метод парабол, или метод Симпсона (рис. 2-3).




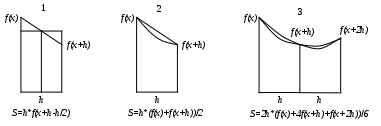
Рис. 2. Графическое представление методов численного интегрирования
Просуммировав площади всех элементарных фигур на интервале [a, b], получаем следующие формулы численного интегрирования:

1. 
   Метод прямоугольников
   

.

2. 
   Метод трапеций
   

.

3. 
   Метод Симпсона
   

.

Разумеется, все эти формулы являются приближенными. С увеличением числа n точность возрастает.

Для оценки правильности принятого алгоритма и составленной по нему программы интегрирования функции рекомендуется провести их проверку на решении следующей тестовой задачи:

при n=32.

Для этого необходимо в программе решения задачи предусмотреть возможность интегрирования наряду с заданной функцией по индивидуальному заданию также и функции f(x)=e^x с пределами интегрирования a=0, b= (=3,141592..=4arctg(1)) и числом n=32.

Тестирование можно считать успешным, если значение интеграла от e^x, вычисленное по разработанной программе, будет совпадать с тестовым с точностью до второго знака.

---

Результаты тестирования должны выводиться наряду с основными результатами интегрирования заданной функции.

3.4. РЕШЕНИЕ ЗАДАЧИ 4

При разработке модуля программы решения нелинейных уравнений необходимо иметь в виду следующие пояснения и рекомендации.

Решение нелинейных уравнений вида F(x)=0 заключается в поиске одного или всех таких значений x на интервале [a,b], при подстановке которых функция F(x) обращается в нуль.

Работу по решению этой задачи целесообразно провести в два этапа.

На первом этапе оценивается характер изменения функции F(x) при изменении аргумента x на интервале [a,b] и проверяется, имеет ли место перемена ее знака (переход через нуль). Количество таких переходов определяет и количество корней.



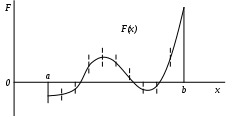
Рис. 3. Графическое представление функции F(x)
Для этого интервал [a,b] разбивается на n участков, где n принимается равным 10..15, и вычисляется функция F(x) на каждом участке, т.е. при изменении x от aдо b с шагом h=(b-a)/n.

Из полученной таким образом таблицы будет виден и характер изменения функции, и количество переходов через нуль.

На втором этапе путем последовательных приближений производится поиск корней одним из предлагаемых методов.

---