Добавлен: 09.11.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МиНИСТЕРСТВО науки и высшего образования
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ»
Институт промышленных технологий и инжиниринга
КАФЕДРА ЭЛЕКТРОЭНЕРГЕТИКИ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к контрольной работе
по дисциплине «Электроника»
Выполнил:
студент группы
Проверила:
Ст. преподаватель каф. КС
Дата защиты_____________ Оценка___________
Тюмень
Задача №1
Сложные логические элементы. Элементы сборки.
Помимо простейших логических элементов в состав стандартных серий входит и несколько более сложных логических элементов. Они представляют собой несложную комбинацию из простейших логических элементов. От более сложных комбинационных микросхем эти элементы отличаются именно очевидной сводимостью к простейшим элементам. Поэтому в справочниках обычно даже не приводятся таблицы истинности этих элементов.
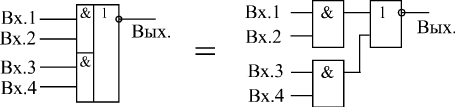
Рис. 1 Логический элемент ЛР1 и его эквивалентная схема
Типичный пример сложного логического элемента — ЛР1. В корпусе микросхемы содержится два элемента, каждый из которых представляет собой комбинацию из двух элементов 2И и одного элемента 2ИЛИ-НЕ (рис.1). По такому же принципу строятся и другие микросхемы ЛР. Разница между ними только в количестве элементов И и в количестве входов этих элементов (рис.2). Некоторые из микросхем ЛР (ЛР1, ЛР3) допускают подключение к специальным входам микросхем расширителей ЛД, хотя такое расширение применяется на практике довольно редко. Микросхема ЛР10 отличается от ЛР9 выходом ОК.
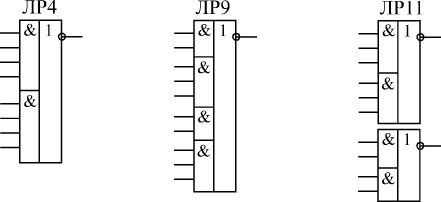
Рис. 2 Примеры логических элементов ЛР
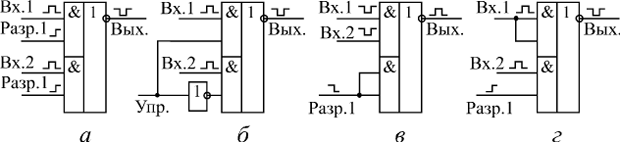
Рис. 3 Примеры использования элементов ЛР1
На рис.3 приведено несколько примеров наиболее типичных применений микросхемы ЛР1. Самое распространенное ее использование (а) состоит в организации двухканального мультиплексирования, то есть в переключении сигналов с двух входов на один выход. При этом один из входов каждого из элементов 2И используется в качестве информационного, а другой — в качестве разрешающего. Вариант этого включения (б) — использование одного управляющего входа переключения каналов и дополнительного инвертора. При единице на управляющем входе работает верхний канал, при нуле — нижний. Еще один вариант использования элемента ЛР1 (в) — смешивание двух отрицательных входных сигналов с возможностью разрешения/запрета выходного сигнала. Наконец, последний показанный на рисунке вариант (г) — смешивание двух положительных сигналов, один из которых может быть разрешен или запрещен. То есть такое объединение в одном элементе функций И и ИЛИ довольно удобно.
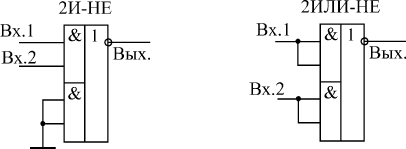
Рис. 4 Использование элементов ЛР в качестве элементов 2И-НЕ и 2ИЛИ-НЕ
На других элементах ЛР можно строить более сложные схемы. Например, элемент ЛР9 позволяет построить четырехканальный мультиплексор, так как в его структуре четыре элемента И и элемент 4ИЛИ-НЕ. Однако в большинстве случаев применение элементов ЛР для мультиплексирования оказывается не слишком удобным, так как в стандартных сериях имеются специальные микросхемы мультиплексоров с более удобным управлением.
При необходимости элементы ЛР1 могут использоваться в качестве более простых элементов 2И-НЕ и 2ИЛИ-НЕ (рис. 4.8). Элемент 2ИЛИ-НЕ получается при попарном объединении входов. Элемент 2И-НЕ получается при отключении половины схемы путем подачи нулей на два входа. При желании можно, конечно, свести элемент ЛР даже к простому инвертору, но это, наверное, уже недопустимая роскошь.
К сложным логическим элементам, помимо ЛР, можно отнести также и элементы И-НЕ с выходом 3С (например, ЛА17 — 4И-НЕ, ЛА19 — 12И-НЕ). Их можно рассматривать как комбинацию обычного элемента И-НЕ и выходного буфера с выходом 3С. Наличие дополнительного управляющего входа EZ и выход 3С создают принципиально новые возможности применения этих элементов. Например, их можно использовать для работы на мультиплексированную или двунаправленную линию, при этом они еще и выполняют функцию И-НЕ над входными сигналами. Но на практике значительно чаще элемент ЛА19 используют как самый обычный элемент 12И-НЕ с выходом 2С, для чего на управляющий вход EZ постоянно подается сигнал логического нуля.
Среди элементов И, ИЛИ, ИЛИ-НЕ элементы с выходом 3С отсутствуют.
Задача №2
Схема трехразрядного суммирующего счетчика импульсов с последовательным переносом на JK-триггерах с шиной сброса.
Счетчик — это устройство, выполняющее функцию счета количества импульсов, поступающих на его вход, и формирующее на выходе число, соответствующее числу импульсов на входе.
Счетчики характеризуются модулем счета и разрядностью. Модуль счета КСИ (коэффициент счета импульсов) — это максимальное число импульсов, которое может быть сосчитано счетчиком, прежде чем произойдет его циклическое обнуление (начальное состояние счетчика включается в цикл счета). Разрядность счетчика определяется разрядностью двоичного числа на выходе счетчика.
Счетчики импульсов можно разделить на следующие классы:
• по направлению счета: суммирующие, вычитающие, реверсивные. Суммирующие — это счетчики, в которых с приходом очередного счетного импульса результат увеличивается на единицу (инкрементируется).
• по способу организации внутренней связи: с последовательным (сквозным) переносом или асинхронные счетчики, параллельные или синхронные счетчики, с комбинированным переносом, кольцевые. Счетчики со сквозным переносом — это счетчики, в которых изменение состояния на выходе происходит путем сквозного переноса информации из самого младшего разряда к старшему, т.е. выходные состояния счетчика изменяются не одновременно, не синхронно с импульсами тактового генератора. В счетчиках с параллельным переносом составные элементы счетчика срабатывают одновременно, т.е. синхронно с тактовыми импульсами. В параллельных счетчиках выходные состояния изменяются одновременно;
Задача №3
Переведите число из десятичной системы счисления в двоичную.
Таблица №1
| № варианта | Число |
| 192 | 66789 |
Решение:
Делим исходное число на основание искомого
числа и записываем остаток до тех пор, пока неполное частное не будет равно нулю. Полученные остатки записываем в обратном порядке.
Деление Целое частное Остаток
66789 / 2 33394 1
33394 / 2 16697 0
16697 / 2 8348 1
8348 / 2 4174 0
4174 / 2 2087 0
2087 / 2 1043 1
1043 / 2 521 1
521 / 2 260 1
260 / 2 130 0
130 / 2 65 0
65 / 2 32 1
32 / 2 16 0
16 / 2 8 0
8 / 2 4 0
4 / 2 2 0
2 / 2 1 0
1 / 2 0 1
Ответ: 6678910(в десятичной) равно = 100000100111001012(в двоичной).
Ответ: 10000010011100101
Задача №4
Переведите число из десятичной системы счисления в шестнадцатеричную.
Таблица №2
| № варианта | Число |
| 192 | 1299 |
Решение:
Делим исходное число на основание искомого числа и записываем остаток до тех пор, пока неполное частное не будет равно нулю. Полученные остатки записываем в обратном порядке.
Деление Целое частное Остаток
1299 / 16 81 3
81 / 16 5 1
5 / 16 0 5
Ответ: 129910(в десятичной) равно = 51316(в шестнадцатеричной).
Ответ - 513
Задача №5
Переведите число из двоичной системы счисления в десятичную
Таблица №3
| № варианта | Число |
| 192 | 100010111 |
Решение:
Каждый разряд исходного числа умножим на его основание в степени n, где n – номер разряда, при этом 0 – самый младший целый разряд. Для дробных разрядов n - отрицательный. Сложим полученные значения.
1000101112 = (1 × 28) + (0 × 27) + (0 × 26) + (0 × 25) + (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 256 + 0 + 0 + 0 + 16 + 0 + 4 + 2 + 1 = 27910
или можно записать так:
Решение:
1000101112 = (20 * 1) + (21 * 1) + (22 * 1) + (23 * 0) + (24 * 1) + (25 * 0) + (26 * 0) + (27 * 0) + (28 * 1) = 20 + 21 + 22 + 24 + 28 = 27910
Ответ: 1000101112(в двоичной) равно = 27910(в десятичной).
Ответ : 279
Задача №6
Переведите число из шестнадцатеричной системы счисления в двоичную.
Таблица №4
| № варианта | Число |
| 192 | 78A1 |
Решение:
Сначала переведем число в десятичную систему счисления:
Каждый разряд исходного числа умножим на его основание в степени n, где n – номер разряда, при этом 0 – самый младший целый разряд. Для дробных разрядов n - отрицательный. Сложим полученные значения.
Буквенные разряды шестнадцатеричного числа заменяем соответствующими числовыми значениями: A – 10.
78A116 = (7 × 163) + (8 × 162) + (10 × 161) + (1 × 160) = 28672 + 2048 + 160 + 1 = 3088110
Затем переведем из десятичной системы в конечную:
Делим исходное число на основание искомого числа и записываем остаток до тех пор, пока неполное частное не будет равно нулю. Полученные остатки записываем в обратном порядке.
Деление Целое частное Остаток
30881 / 2 15440 1
15440 / 2 7720 0
7720 / 2 3860 0
3860 / 2 1930 0
1930 / 2 965 0
965 / 2 482 1
482 / 2 241 0
241 / 2 120 1
120 / 2 60 0
60 / 2 30 0
30 / 2 15 0
15 / 2 7 1
7 / 2 3 1
3 / 2 1 1
1 / 2 0 1
3088110 = 1111000101000012
Ответ : = 111100010100001