ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2021
Просмотров: 884
Скачиваний: 4
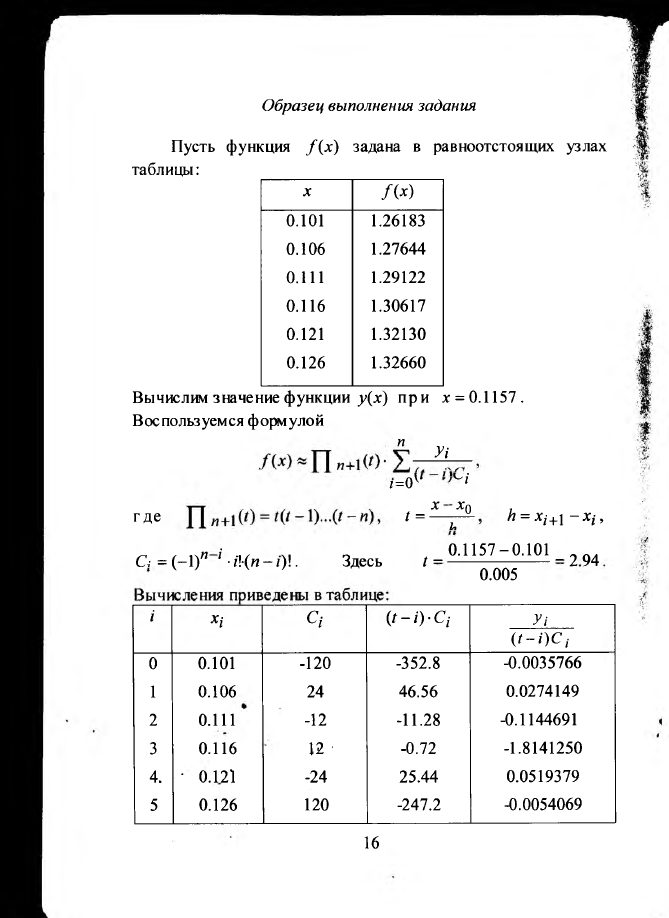
Образец выполнения задания
Пусть функция / ( лс) задана в равноотстоящих узлах
таблицы:
*
f i x )
0.101
0.106
0.111
0.116
0.121
0.126
1.26183
1.27644
1.29122
1.30617
1.32130
1.32660
Вычислим значение функции >>(*) п р и * = 0.1157.
В ос польз уем ся ф орм уло й
"
У1
г=0м
” w
г д е
=
t = ^—^
С; = (-Y)n i
• /!•(« - /)!.
Здесь
h = x
i+1
- x t ,
t _
0.1157-0.101 _ 2 94
0.005
i
x t
Q
( t - i ) - C i
У1
( t - i ) C i
0
0.101
-120
-352.8
-0.0035766
1
0.106
24
46.56
0.0274149
2
0.111
-12
-11.28
-0.1144691
3
0.116
12 ■
-0.72
-1.8141250
4.
• 0.121
-24
25.44
0.0519379
5
0.126
120
-247.2
-0.0054069
16
Итак, П 6 (0 = -0.7024271, £ —
г = —1.858225 .
^ ( ' - О б
следователь но, /(0.1157) *1.30527.
Лабораторная работа №4
ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ
МНОГОЧЛЕНОВ НЬЮТОНА
Задание.
Выполнить задание лабораторной работы №3,
используя вместо многочлена Лагранжа многочлены
Ньютона.
Образец выполненш заданш
Используя
первую
или
вторую
интерполяционную
формулу Ньютона, вычислим значения функции
у ( х
) при
следующих значениях аргумента:
1)
х х
=1.2273;
2) *2 =1.253;
3) х3 =1.210;
4) *4 =1.2638.
X
У
1.215
0.106044
' 1.220
0.113276
1.225
0.119671
1.230
0.125324
1.235
0.130328
1.240
0.134776
1.245
0.138759
1.250
0.142367
1.255
0.145688
1.260
0.14809
17

Составим таблицу конечных разностей:
Xi
У1
A
yt
А
2У{
Л3. ,
1.215
0.106044
0.007232
-0.000837
0.000095
1.220
0.113276
0.006395
-0.000742
0.000093
1.225
0.119671
0.005653
-0.000649
0.000093
1.230
0.125324
0.005004
-0.000556
0.000091
1.235
0.130328
0.004448
-0.000465
0.000090
1.240
0.134776
0.003983
-0.000375
0.000088
1.245
0.138759
0.003608
-0.000287
0.000087
1.250
0.142367
0.003321
-0.000200
1.255
0.145688
0.003121
1.260
0.14809
При
составлении
таблицы
конечных
разностей
ограничиваемся разностями третьего порядка, так как они
практически постоянны. Для вычисления значений функции
при * = 1.2273 и
jc
= 1.210 воспользуемся формулой Ньютона
для интерполирования вперед:
/ ч
*
— 1) а2
а
з
У( х ) х У0 + ЯАУ0
+ —
у
—
Уо +
--------
3
!--------
Уо’
x
-
xq
где
q
= — —^- .
h
1) Если
jc
= 1.2273, то примем
jcq
= 1.225; тогда
1.2273-1.225
а
= ------------------ = 0.46,
4
0.005
у{
1.2273) * 0.119671+0.46 • 0.005653+ 0 4^
5-4i (-0.000649) +
+ Q46(~Q54)(~1-5j ) 0.000093 = 0.119671+0.0026004+ 0.000806+
6
+ 0.0000059= 0.1223579* 0.12235&
2) Если
х
=1.210, то примем jcq = 1.215; тогда
1.210-1.215
q =
---------------- = - 1 ,
0.005
>-(1.210) * 0.1106044 + (-1) • 0.007232 +
(-0.000837) +
+ (-~ 1)(~2)(~3) 0.000095 = 0.097880.
Для вычисления значений функции при * = 1.253 и
* = 1.2638
воспользуемся
формулой
Ньютона
для
интерполирования назад:
, „д..
.9 ( 9 + 1) *2..
,
q(q + l)(q + 2)
д3
У\Х) ~ у п + qt\yn _\ +
2
J
Уп-2
+
Уп-Ъ->
* - * „
где
q
=
h
3) Если * = 1.253, то примем
х п
=1.255; тогда
1.253-1.255
Л/1
q
= ---------------- = -0 .4 ,
0.005
у (
1.253) * 0.145688 + (-0.4) • 0.003321 + (~ °-* )'°-6 (-0.000287) +
+ ( - ° :4) ' 0;6 ' 1 6 0.000088 = 0.1443884 * 0.144388.
4) Если * = 1.2638, то примем
х п
= 1.260; тогда
1.2638-0.260
9 = ------------------ = 0.76,
0.005
у{\
.2638) * 0.148809 + 0.76 • 0.003121 + 0-76^176 (-0.000200)
л
HtL
1
П(\ 'У Н£ь
+ - — —— —— 0.000087 = 0.1511007 « 0.151101.
19
Лабораторная работа №5
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Задание.
Используя метод наименьших квадратов, подобрать
для заданных значений
х и у
1) линейную функцию
у - A
q
+ А ^х
;
2
2) квадратичную функцию
у =
A
q
+ А\х
+
А2х .
№
1
.
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Y
0.740
0.532
0.801
1.13
0.749
0.772
0.749
№
2
.
X
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Y
1.33
0.912
0.755
0.966
0.524
0.574
0.824
№3.
5.0
5.5
6.0
6.5
7.0
7.5
8.0
Y
0.741
0.848
0.809
0.854
0.801
1.04
1.44
№4.
X
4.0
4.5
5.0
5.5
6.0
6.5
7.0
Y
0.567
0.759
0.991
1.57
0.532
0.634
1.24
№5.
X
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Y
1.59
0.935
0.596
1.78
0.682
0.946
0.584
№6.
№7.
X
5.0
5.5
6.0
6.5
7.0
7.5
8.0
Y
0.707
0.790
1.11
0.674
0.948
0.516
0.662
X
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Y
0.751
0.964
0.927
0.780
0.585
0.756
0.846
№8.
X
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Y
0.622
0.720
1.05
0.831
1.69
0.705
0.830
20