ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2021
Просмотров: 883
Скачиваний: 4
№
10
.
№
11
.
№
12
.
№13.
№14.
№15.
№16.
№17.
№18.
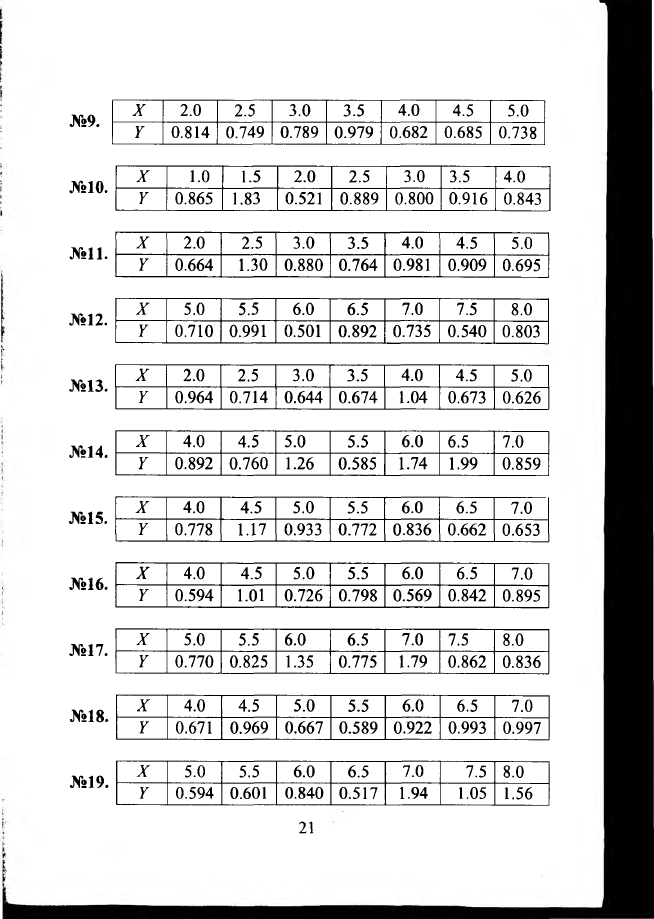
№9.
№ 19.
X
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Y
0.814
0.749
0.789
0.979
0.682
0.685
0.738
X
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Y
0.964
0.714
0.644
0.674
1.04
0.673
0.626
X
4.0
4.5
5.0
5.5
6.0
6.5
7.0
Y
0.778
1.17
0.933
0.772
0.836
0.662
0.653
X
5.0
5.5
6.0
6.5
7.0
7.5
8.0
Y
0.770
0.825
1.35
0.775
1.79
0.862
0.836
X
4.0
4.5
5.0
5.5
6.0
6.5
7.0
Y
0.594
1.01
0.726
0.798
0.569
0.842
0.895
X
4.0
4.5
5.0
5.5
6.0
6.5
7.0
Y
0.892
0.760
1.26
0.585
1.74
1.99
0.859
X
5.0
5.5
6.0
6.5
7.0
7.5
8.0
Y
0.710
0.991
0.501
0.892
0.735
0.540
0.803
X
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Y
0.664
1.30
0.880
0.764
0.981
0.909
0.695
X
1.0
1.5
2.0
2.5
3.0
3.5
4.0
Y
0.865
1.83
0.521
0.889
0.800
0.916
0.843
X
4.0
4.5
5.0
5.5
6.0
6.5
7.0
Y
0.671
0.969
0.667
0.589
0.922
0.993
0.997
X
5.0
5.5
6.0
6.5
7.0
7.5
8.0
Y
0.594
0.601
0.840
0.517
1.94
1.05
1.56
21
X
3.0
3.5
4.0
4.5
5.0
5.5
6.0
Y
1.19
0.671
0.542
0.750
0.775
1.82
0.651
Образец выполнения задания
Пусть на основании эксперимента получены
значения
функции
у =
/ (
х ),
которые записаны в таблице:
X
0.5
1.0
1.5
2.0
2.5
3.0
У
0.31
0.82
1.29
1.85
2.51
3.02
Аппроксимируем таблично заданную функцию
у = т
линейной
у
- A
q
+A
i x
с помощью метода наименьших
квадратов.
Составим систему для определения
A
q
, А\
6
6
А0т + А{
=
^ У к
к=
1
к=\
6
6
6
А0 Y . x k + А1 Ц х к = Z х кУк-
к -
1
к=
1
к=
1
Предварительно вычисляем
6
Y ^ x k
=0.5 + 1 + 1.5 + 2 + 2.5 + 3 = 10.5,
к=\
6
=0.25 + 1 + 2.25 + 4 + 6.25 + 9 = 22.75,
к=\
6
^ У к =
0.31 + 0.82 +1.29 +1.85 + 2.51 + 3.02 = 9.8,
Y /к У к
= 0.5-0.31+1-0.82+1.5-1.29+2-1.85+2.5-2.51+3-3.02=21.94
к=\
[6 ^ 0 + 1 0 .5 ^ = 9.8
[10.5Л0
+22.15АХ -
21.94.
Решая эту систему, находим
A
q
и
А \
:
A
q
= -0 .2 8 ,
А\
=1.09.
Искомый многочлен
у
= 1.09* + 0.28.
Следовательно,
Лабораторная работа №6
ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ
Задание.
Найти решение системы линейных уравнений по
формулам Крамера, методом Гаусса без выбора
ведущего элемента и методом Гаусса с выбором
ведущего элемента по столбцу. Сравнить количество
операций.
№
1
.
9
jcj
+ 4
jc
2 - 4
дг
4 = -2 ,
5*( + 7
л
:2 - * 4 = 2 ,
5*! - 5*2 +12*з
~ х 4
= 5,
4 * j + 5 * 2 - 4 * з + 1 4 * 4 ~ - 3.
№2.
14*j + 4*2 - 4*3 + 5*4 = 2,
2*] +11*2 + 3*з + 5*4 = 4,
— 5*j +7*з
+*4
—
3,
-3 * | -3*2 —
*3
+
8*4
- -5.
№3.
6
*j -
3*2
—*3
—
*4
= -2,
4*j +14*2 +4*з +5*4 =-3,
-4*j +
2*2
+11*з -
4*4
=4,
3*| —
*2
+3*з +
8*4
=3.
№4.
11*] + 5*2 - 2*з + 3*4 = -2,
*! + 1 0 *2 + 3*3 - 5*4 = -5 ,
4 *j - 4*2 + 1 1*з -
2*4
= 1,
*! + 2*2 - 5*з + 9*4 = -4 .
№5.
8*] - х2
+
3x3 + Зх4 = -1,
- 2лГ] +
5х2 -
2х3
= 5,
—
2xj —
2х2 + 7х3 +
2
х
4 =
—4,
-4л:]
+ х2
- 4 х 3 + 10х4 - -1.
№
6
.
12х, + 5х2 + 5х3 - х 4
- 2 ,
5jc, + 1 1х2 + 5лг3 = 5,
2хх
+ 4jc2 +
12х3 + 5
х
4 =1,
Зх] - х 2 +Зх3 +8х4 =3.
№7.
12Х] + 4
х
2
-З х 3
- 4
х
4 =1,
3xj +1 (к2 - 5х3 - х4 = -4,
-4 х , - 2
х
2 +12х3 - 5
х
4 = -5 ,
-3 x j - 5 х 3 +9
х
4 = -1 .
№
8
.
10xj - З х 2 +4х3
- 2
х
4
= -1,
4х2 +2х3 +х4 = —
3,
3xj +8х3
- 4
х
4
=3,
Зх] - х 2 -З х 3 +8х4
- 2 .
№9.
9х, - 2х2 - Зх3 - Зх4 - 3,
Эх, +7
х
2 +2
х
3 +
х
4 =3,
3xt +4
х
2 +9х3 - х 4 =5,
ЗХ] - 5
х
2 - 5х3 +1 4
х
4 - 5.
№
10
.
IQxj
- 2
х
2
+Зх3
- 4
х
4 = -5 ,
-X] +9
х
2 +2
х
3 - 5
х
4 =3,
-4 x j
+3х2 +К к3
+2
х
4 =-1,
-4х] - 5
х
2
+Зх3
+13
х
4 = -5 .
№ 11.
9xj +
2
х
2 - х3 - 5
х
4
=
-4,
- X) + 4
х
2 -
х3 - х4
= 2,
- Xj + 4
х
2 + 6х3 = -4 ,
х2 - 5х3 + 7
х
4 - -4 .
№12.
1 к] - 5
х
2 - 4
х
3 —
х4
=3,
Зх2 — х3 - х 4
- - 4 ,
-5х,
- 4 х 2 +14х3 +4х4
=
-4,
-4xj —
х2 -5 х 3 +11х4 = -3.
№13.
бХ] - 2
х
2 -2 х 3 — х4 =0,
5xj +12
х
2 +5
х
3
+х4
=-2,
-5Х| +5
х
2 +13х3 - 2
х
4 =4,
-4 х , - 4
х
2
-З х 3
+12
х
4
- - 2 .
№14.
8xj + х 2 - х 3
- 5
х
4 = 5,
—
Х[
+ 7х2
- З
х
3
+2х4 =1,
Зх) + 3х2 + 1 (к 3 - З х 4 = - 3 ,
-5 х ] + 3 х 2 + 2 х 3 + 1 1х4 = 1.
24
№15.
№17.
№19.
1 CbC] + 2x2 - 2
x
3 - 5
x
4 = 4 ,
X] +4x2 + 2
x
4 = -5,
-2X[ -5 x 2 + 12x3 +4x4
= 0 ,
4x| - 3 x 2 - 4 x 3 +12x4 =1.
8xj +4x3 -3 x 4 =0,
— 5X| +1 lx2 —x3 + 4
x
4 = 4,
-3 x ] - x 2 + 6 x 3 - x 4 = 2 ,
-5 x j - 3 x 2 - 4 x 3 +13x:4 = - 1 .
Kkj - 2 x 2 +2x3 - 5 x 4 =3,
8
x
2 + 4 x 3 + 3 4 = 0 ,
5 x ,
- 2 x 2 +12x3 - 4 x 4 =1,
2xj - 4 x 2 - 4 x 3 +1
l x 4
= 1.
№16.
№18.
1QX] - 4
x
2 + 3
x
3 + 2
x
4 = 3,
4x] +10bc2 + 4 x 3 + x 4 = -1 ,
X[ - 4x2 + 6x3 - 3x4 = 1,
-X ! - x 2 - 3 x 3 + 6 x 4 = - 1 .
13xj + 3 x 2 - 5 x 3 - 5
x
4 = 0 ,
4xj + 8 2 - 3 x 3 - 2,
4
x
2 + 7
x
3 - 2
x
4 = 3,
3x] + 2
x
2 + 2
x
3 +8
x
4 = 2.
№20.
8x|
- 4
x
2 +
x
3 + 2
x
4
= 5,
-3x, +1 lx2 -5 x 3
- 2
x
4 = -2 ,
4xj
+ 5
x
2
+1 Qx3 = -3,
3x] +3x2 -3 x 3 +10x4 =4.
Образец выполненш заданш
Правило Крамера
П усть дана систем а линейны х уравнений
2xj + х 2 - 2 х 3 + х4 =1,
3xt + 4
х
2 + х 3 - Зх4 = - 7 ,
4Х| - 2
х
2 + Зх3 - 4
х
4 = 3,
2х] + 2
х
2 - Зх3 - х 4 = - 1 1 .
Вы числяем определители
2
1
- 2
1
0
1
0
0
- 5
4
- 7
3
4
1
- 3
- 5
4
4
- 7
А =
—
=
—
8
7
- 2
4
- 2
3
- 4
8
- 2
7
- 2
- 2
-1
- 3
2
2
- 3
-1
- 2
2
-1
- 3
= -(105 +16 + 56 - 98 +10 + 96) = -185;
25