Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное

учреждение высшего образования

Тульский государственный университет

Кафедра «Инструментальные и метрологические системы»

МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ

Лабораторная работа № М1
Оценка результатов нескольких серий измерений
Методические указания

Тула 2020

1. Цель работы

- получение практических навыков выполнения измерений;

- ознакомление с вероятностным подходом к оценке результатов измерений;

- получение навыков обработки результатов нескольких серий измерений.

2. 
   Теоретические положения
   

2.1. Оценка результатов измерений как случайных величин

При проведении с одинаковой тщательностью и в одинаковых условиях повторных измерений одной и той же неизменяющейся величины мы получаем результаты, некоторые из которых отличаются друг от друга, а некоторые совпадают. Такие результаты говорят о наличии в них случайных погрешностей, то есть погрешностей, изменяющихся хаотически, непредсказуемо.

Рассмотрение случайных погрешностей (и, соответственно, результатов однократных измерений) как случайных событий дает основание использовать математический аппарат теории вероятностей и математической статистики для оценки случайных погрешностей и нахождения значения измеряемой величины, более близкого к истинному значению, чем результат одного измерения.

Теория вероятностей называет случайным такое событие, которое может произойти или не произойти. Применительно к измерениям можно сказать, что при повторных измерениях в одинаковых условиях каждая из множества возможных незначительных причин случайных изменений результатов может или появиться, или не появиться. Количественная оценка объективной возможности появления события называется его вероятностью. Вероятность достоверного события равна 1, а вероятность невозможного события - 0. Эти события неслучайные; для случайных событий вероятности их появления больше нуля и меньше единицы.

---

Наиболее универсальным способом описания случайных величин (в том числе результатов измерений и случайных погрешностей) являются законы распределения вероятности. Законом распределения вероятности случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Если на процесс измерения действуют несколько влияющих факторов, а вклад каждого из факторов незначителен по сравнению с их суммарным воздействием, то, согласно центральной предельной теореме теории вероятностей, результат измерения физической величины X подчиняетсянормальному закону или закону Гаусса.

На рис. 1 показаны кривые плотности вероятности или дифференциальной функции нормального распределения. Аналитически эта функция описывается выражением

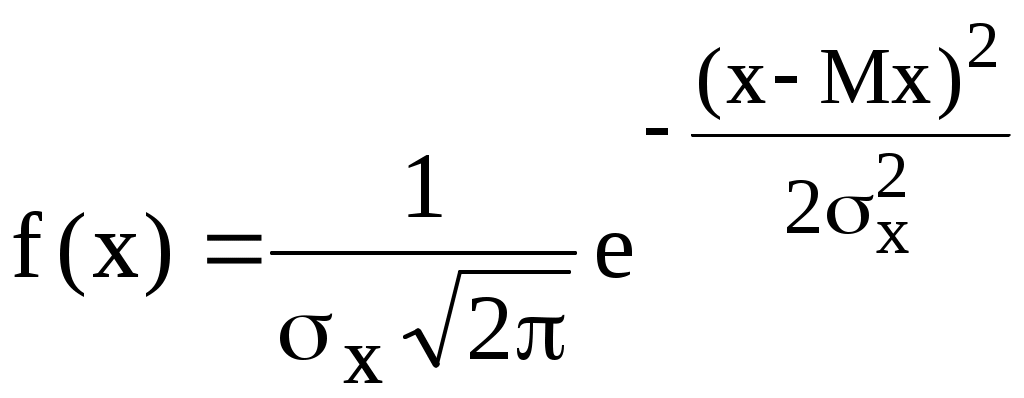, (1)

где Мх - математическое ожидание случайной величины Х,

σ_x - среднее квадратическое отклонение (СКО) случайной величины.



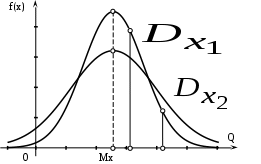
Рис.1. Кривые функций нормального распределения.

Математическим ожиданием(Мх) случайной величины Х называется такое её значение, вокруг которого группируются результаты отдельных наблюдений; при нормальном распределении математическому ожиданию соответствует наибольшая плотность вероятности.

Статистической оценкой математического ожидания для ряда однородных результатов является среднее арифметическое:

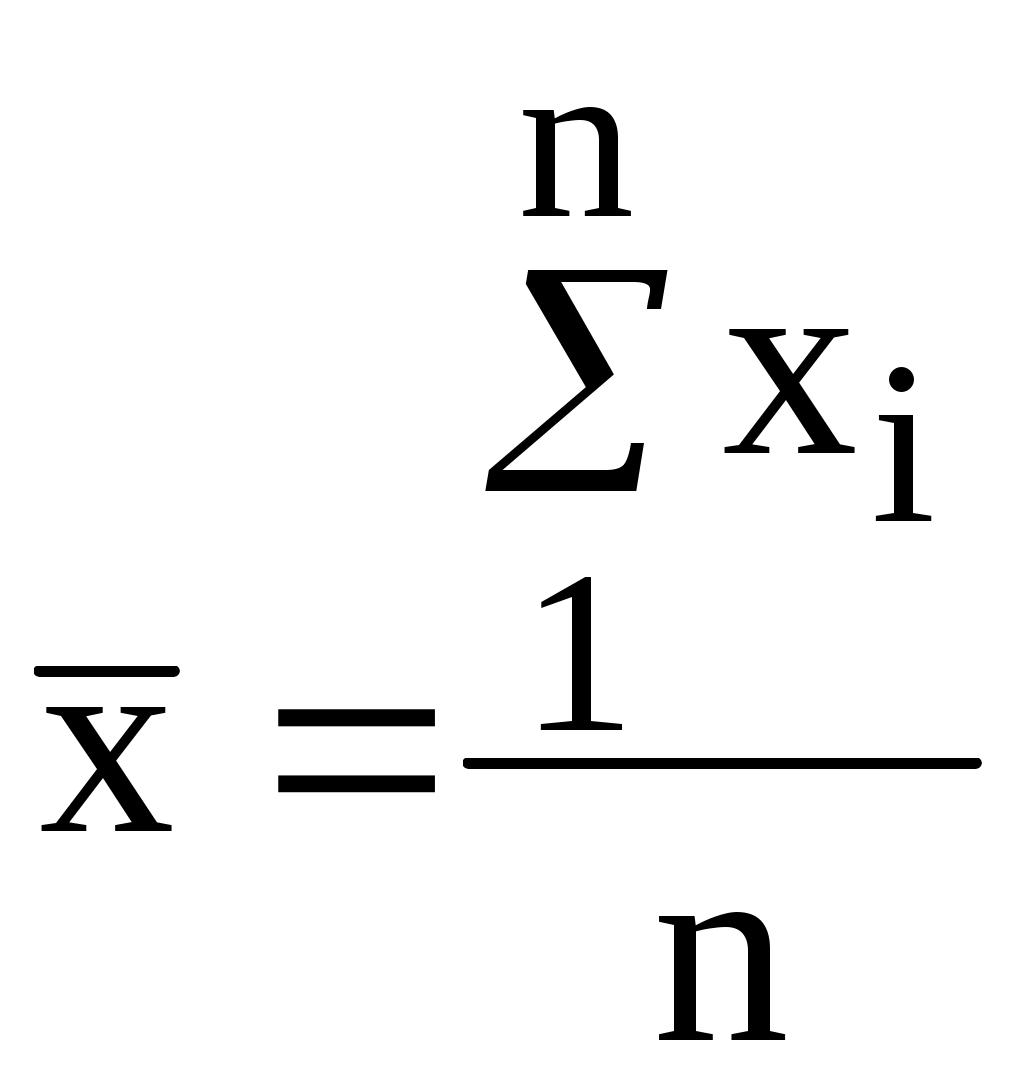. (2)

Среднее квадратическое отклонение (СКО) _x случайной величины представляет собой меру рассеивания значений случайной величины относительно её математического ожидания

,

где D_x - дисперсия случайной величины:

Чем больше дисперсия (или среднее квадратическое отклонение), тем значительнее рассеивание. Например, Dx₂  Dx₁ (рис.1).

Статистической оценкой СКО является так называемое стандартное отклонение:

, (3)

где n - число наблюдений (измерений).

Вероятность попадания случайной величины в интервал (х

---

₁, х₂) равна:

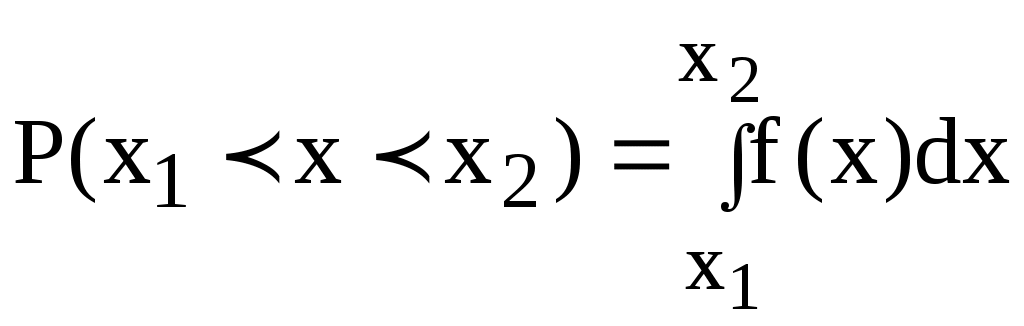, (4)

что соответствует площади под кривой распределения на этом участке (рис.1).

Интервал , который с заданной вероятностью Р покрывает истинное значение случайной величины, называется доверительным интервалом, а вероятность Р - доверительной вероятностью. Как правило, доверительный интервал ε располагается симметрично по отношению к математическому ожиданию.

Отношение доверительного интервала к среднему квадратическому отклонению - это относительный доверительный интервал:

(5)

При достаточно большом числе наблюдений (измерений) вычисленное стандартное отклонение близко к действительному значению среднего квадратического отклонения. Если при этом установлено, что закон распределения вероятности результатов измерения - нормальный, то для нахождения относительного доверительного интервала по доверительной вероятности (и наоборот, доверительной вероятности по относительному доверительному интервалу) используются математические таблицы специальной функции Лапласа. Аргументом функции Лапласа является относительный доверительный интервал, рассчитываемый по формуле:

(6)

Однако действия с функцией Лапласа оказываются тем менее надежными, чем меньше число наблюдений. В подобных случаях следует определять доверительную вероятность или доверительный интервал по таблицам распределения Стьюдента, в зависимости от доверительной вероятности и числа наблюдений (табл.2 приложения).
2.2. Обработка результатов многократных измерений

Многократные измерения одной и той же величины постоянного размера производятся при повышенных требованиях к точности измерений. Результат многократных измерений описывается выражением:

. (7)

Как и результат однократного измерения, он является случайным значением измеряемой величины, но его дисперсия в n раз меньше дисперсии результата однократного измерения:

, соответственно

---

(8)

То есть точность определения значения измеряемой величины повышается в раз.

Результат многократных измерений записывается в форме доверительного интервала

, (9)

где величина t находится в зависимости от заданной доверительной вероятности.

При проведении многократных измерений некоторые результаты могут содержать грубые погрешности, то есть погрешности, явно превышающие по своему значению погрешности, оправданные условиями проведения эксперимента (измерения). Очевидно, что наиболее подозрительными являются минимальное и максимальное показания. Вопрос о том, содержит ли данный результат грубую погрешность, решается общими методами проверки статистических гипотез.

Проверяемая гипотеза состоит в утверждении, что результат х_i не содержит грубой погрешности. Для проверки этой гипотезы при небольшом числе наблюдений используют распределения следующих величин:

, (10)

. (11)

Эти функции совпадают между собой, и для нормального распределения результатов измерения они протабулированы. По табл.1 приложения по заданной доверительной вероятности Р и количестве измерений в серии n находят табличное (предельно допустимое) значение _т; его сравнивают с расчетным значением _р. Если выполняется условие _р  _т , то гипотеза об отсутствии грубой погрешности принимается с вероятностью Р.

После того, как грубые погрешности (промахи) исключены из результатов измерения, необходимо снова определить оценки числовых характеристик и вновь убедиться в отсутствии грубых погрешностей.
2.3.Однородные и неоднородныесерии измерений

Часто измерительная процедура бывает организована таким образом, что с помощью каждого средства измерений получают ряд значений отсчета - серию измерений. При этом могут получаться как однородные, так и неоднородные серии.

Однородными сериями измерений называются такие, у которых распределение вероятности результатов измерений подчиняется одному закону. На практике однородными считают такие серии измерений, у которых числовые характеристики законов распределения вероятности (ЗРВ)

---

и отличаются случайным образом. Если хотя бы одна из этих числовых характеристик отличается от характеристик других серий неслучайно, то эти серии считаются неоднородными.

При неслучайном различии средних результаты серий измерений не подлежат совместной обработке, так как результаты измерений не сходятся. Обычно причиной расхождения является неисключенная систематическая погрешность или резко изменившиеся условия измерений. Однако поскольку при выполнении данной лабораторной работы ни одно из этих обстоятельств не возникает, то выполнять проверку сходимости средних в данном случае не предусматривается.

При неслучайном различии дисперсий серии измерений являются неравноточными (неравнорассеянными).

Результаты равноточных и неравноточных серий измерений подлежат совместной обработке, но по различным методикам. Поэтому перед тем, как приступить к обработке результатов нескольких серий измерений, необходимо произвести проверку их равноточности.

Чаще всего для проверки равноточности дисперсий используют критерий Фишера.

Критерий Фишера определяется по формуле:

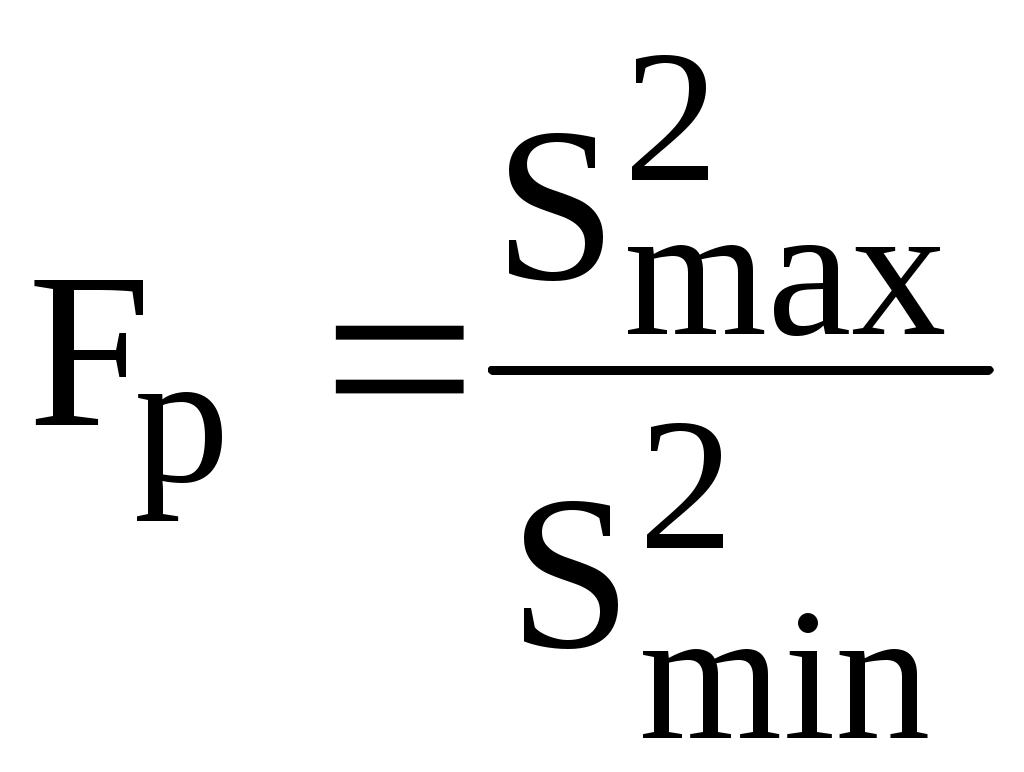, (12)

где F_р - расчетное значение критерия Фишера,

- наибольшая и наименьшая дисперсии из всех серий.

Если выполняется условие

, (13)

то дисперсии - однородны. Следовательно, остальные дисперсии однородны тем более.

Критическое (табличное) значение F-критерия F_T выбирается по табл. 3 приложения в зависимости от доверительной вероятности Р и числа степеней свободы k₁ = n₁ - 1, k₂ = n₂ – 1, где k₁ и k₂ - числа степеней свободы для наибольшей и наименьшей дисперсий соответственно.
2.4. Обработка результатов нескольких серий измерений

---

Смотрите также файлы

• 1. Изучение и расчет параметров системы управления запасами.doc

• Игры гештальттерапии.pdf

• Практическая работа Работа с таблицами Тема Создание и форматирование таблиц в документе ms word. Цель.pdf

• орытынды аттестаттауды ткізуді лгілік аидаларын бекіту туралы.pptx

• Методические указания к лабораторной работе по дисциплине "Электроника" для студентов специальности 220100.doc