Проверяем выполнение условия _р _т.

Табличное предельно допустимое значение _т находим по табл. 1 приложения при доверительной вероятности Р = 0,95 и количестве измерений n = 6

_т =1,996.

Условие _р _т выполняется, следовательно грубых промахов нет.

4. Проверим однородность дисперсий серий измерений, используя критерий Фишера.

Должно выполняться условие:

.

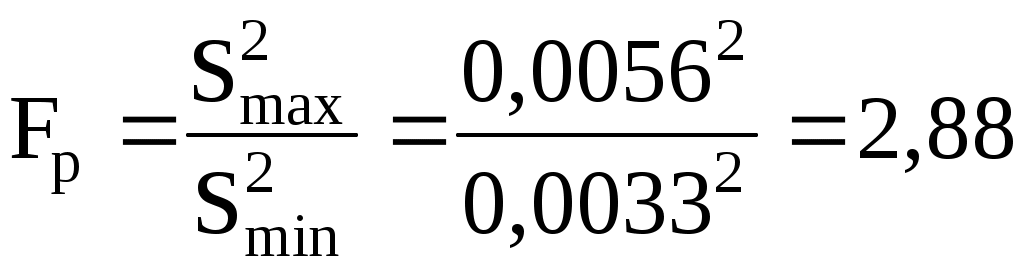F_т = 5,05 – критическое значение F – критерия, выбираемое из табл. 3 приложения в зависимости от Р и числа степеней свободы k₁ и k₂ для наибольшей и наименьший дисперсий.

Условие выполняется, следовательно, серии измерений однородны и равноточны, их можно объединить в единый массив и обрабатывать как результаты многократных равноточных измерений.

5. Определяем:

, где m=2.

, S_x = 0,0046
Окончательный результат записываем в форме доверительного интервала:

, где , .

Значение t выбирается из табл. 2 приложения по доверительной вероятности Р = 0,95 и числу степеней свободы N-1= 11; t = 2,20

Окончательно:

24,9504  x 24,9706

Примечание. При округлении доверительные границы погрешности (стандартного отклонения) должны быть представлены не более, чем двумя значащими цифрами. Значение результата измерения должно оканчиваться цифрами того же разряда, что и значение погрешности.

Дата

Подпись руководителя

П Р И Л О Ж Е Н И Я

Табл. 1

ν

---

- критерий для проверки наличия грубых

промахов в результатах измерения

n	Уровень значимости 1 – P				n	Уровень значимости 1 – P
	0,10	0,05	0,025	0,01		0,10	0,05	0,025	0,01
3	1,406	1,412	1,414	1,414	14	2,297	2,461	2,602	2,759
4	1,645	1,689	1,710	1,723	15	2,326	2,493	2,638	2,808
5	1,731	1,869	1,917	1,955	16	2,354	2,523	2,670	2,837
6	1,894	1,996	2,067	2,130	17	2,380	2,551	2,701	2,871
7	1,974	2,093	2,182	2,265	18	2,404	2,577	2,728	2,903
8	2,041	2,172	2,273	2,374	19	2,426	2,600	2,754	2,932
9	2,097	2,237	2,349	2,464	20	2,447	2,623	2,778	2,959
10	2,146	2,294	2,414	2,540	21	2,467	2,644	2,801	2,984
11	2,190	2,383	2,470	2,606	22	2,486	2,664	2,823	3,008
12	2,229	2,387	2,519	2,663	23	2,504	2,683	2,843	3,030
13	2,264	2,426	2,562	2,714	24	2,520	2,701	2,862	3,051
					25	2,537	2,717	2,880	3,071

---

P – значение доверительной вероятности

Распределение Стьюдента Табл. 2.

P	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99	0,999	P
k														k
1	0,158	0,325	0,510	0,727	1,000	1,376	1,963	3,08	6,31	12,71	31,8	63,7	63,7	1
2	142	289	445	617	0,816	1,061	1,336	1,886	2,92	4,30	6,96	9,92	31,6	2
3	137	277	424	584	765	0,978	1,250	1,638	2,35	3,18	4,54	5,84	12,94	3
4	134	271	414	569	741	941	1,190	1,533	2,13	2,77	3,75	4,60	8,61	4
5	132	267	408	559	727	920	1,156	1,476	2,02	2,57	3,36	4,03	6,86	5
6	131	265	404	553	718	906	1,134	1,440	1,943	2,45	3,14	4,71	5,96	6
7	130	263	402	549	711	896	1,119	1,415	1,895	2,36	3,00	3,50	5,40	7
8	130	262	399	546	706	889	1,108	1,397	1,86	2,31	2,90	3,36	5,04	8
9	129	261	398	543	703	883	1,100	1,383	1,833	2,26	2,82	3,25	4,78	9
10	129	260	397	542	700	879	1,093	1,372	1,812	2,23	2,76	3,17	4,59	10
11	129	260	396	540	697	876	1,088	1,363	1,796	2,20	2,72	3,11	4,49	11
12	128	259	395	539	695	873	1,083	1,356	1,782	2,18	2,68	3,06	4,32	12
13	128	259	394	538	694	870	1,079	1,350	1,771	2,16	2,65	3,01	4,22	13
14	128	258	393	537	692	868	1,076	1,345	1,761	2,14	2,62	2,98	4,14	14
15	128	258	393	536	691	866	1,074	1,341	1,753	2,13	2,60	2,95	4,07	15
16	128	258	392	535	690	865	1,071	1,337	1,746	2,12	2,58	2,92	4,02	16
17	128	257	392	534	689	863	1,069	1,333	1,740	2,11	2,57	2,90	3,96	17
18	127	257	392	534	688	862	1,067	1,330	1,734	2,10	2,55	2,88	3,92	18
19	127	257	391	533	688	861	1,066	1,328	1,729	2,09	2,54	2,86	3,88	19
20	127	257	391	533	687	860	1,064	1,325	1,725	2,09	2,53	2,84	3,85	20
21	127	257	391	532	686	859	1,063	1,323	1,721	2,08	2,52	2,83	3,82	21
22	127	256	390	532	686	858	1,061	1,321	1,717	2,07	2,51	2,82	3,79	22
23	127	256	390	532	685	858	1,060	1,319	1,714	2,07	2,50	2,81	3,77	23
24	127	256	390	531	685	857	1,059	1,318	1,711	2,06	2,49	2,80	3,74	24
25	127	256	390	531	684	856	1,058	1,316	1,708	2,06	2,48	2,79	3,72	25
26	127	256	390	531	684	856	1,058	1,315	1,706	2,06	2,48	2,78	3,71	26
27	127	256	389	531	684	855	1,057	1,314	1,703	2,05	2,47	2,77	3,69	27
28	127	256	389	530	683	855	1,056	1,313	1,701	2,05	2,47	2,76	3,67	28
29	127	256	389	530	683	854	1,055	1,311	1,699	2,04	2,46	2,76	3,66	29
30	127	256	389	530	683	854	1,055	1,310	1,697	2,04	2,46	2,75	3,65	30

---

Табл. 3.

---

Распределение Фишера

При доверительной вероятности 0,95 (обычный шрифт) и 0,99 (жирный шрифт)

	k2	k1 – степени свободы для большей дисперсии																		k2
k2 – степени свободы меньшей дисперсии		1	2	3	4	5	6	7	8	9	10	11	12	14	16	20	24	30	40
	1	161	200	216	225	230	234	237	239	241	242	243	244	245	246	248	249	250	251	1
		4052	4999	5403	5625	5764	5889	5928	5981	6022	6056	6082	6106	6142	6169	6208	6234	6258	6286
	2	18,51	19,00	19,16	19,25	19,30	19,33	19,36	19,37	19,38	19,39	19,40	19,41	19,42	19,43	19,44	19,45	19,46	19,47	2
		98,49	99,01	99,17	99,25	99,30	99,33	99,34	99,36	99,38	99,40	99,41	99,42	99,43	99,44	99,45	99,46	99,47	99,48
	3	10,13	9,55	9,28	9,12	9,01	8,94	8,88	8,84	8,81	8,78	8,76	8,74	8,71	8,69	8,66	8,64	8,62	8,60	3
		34,12	30,81	29,46	28,71	28,24	27,91	27,67	27,49	27,34	27,23	27,13	27,05	26,92	26,83	26,69	26,60	26,50	26,41
	4	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04	6,00	5,96	5,93	5,91	5,87	5,84	5,80	5,77	5,74	5,71	4
		21,20	18,00	16,69	15,98	15,52	15,21	14,98	14,80	14,66	14,54	14,45	14,37	14,24	14,15	14,02	13,93	13,83	13,74
	5	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82	4,78	4,74	4,70	4,68	4,64	4,60	4,56	4,53	4,50	4,46	5
		16,26	13,27	12,06	11,39	10,97	10,67	10,45	10,27	10,15	10,05	9,96	9,89	9,77	9,68	9,55	9,47	9,38	9,29
	6	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15	4,10	4,06	4,03	4,00	3,96	3,92	3,87	3,84	3,81	3,77	6
		13,74	10,92	9,78	9,15	8,75	8,47	8,26	8,10	7,98	7,87	7,79	7,72	7,60	7,52	7,39	7,31	7,23	7,14
	7	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73	3,68	3,63	3,60	3,57	3,52	3,49	3,44	3,41	3,38	3,34	7
		12,25	9,55	8,45	7,85	7,46	7,19	7,00	6,84	6,71	6,62	6,54	6,47	6,35	6,27	6,15	6,07	5,98	5,90
	8	5,32	4,46	4,07	3,84	3,69	3,58	3,50	3,44	3,39	3,34	3,31	3,28	3,23	3,20	3,15	3,12	3,08	3,05	8
		11,26	8,65	7,59	7,01	6,63	6,37	6,19	6,03	5,91	5,82	5,74	5,67	5,56	5,48	5,36	5,28	5,20	5,11
	9	5,12	4,26	3,86	3,63	3,48	3,37	3,29	3,23	3,18	3,13	3,10	3,07	3,02	2,98	2,93	2,90	2,86	2,82	9
		10,56	8,02	6,99	6,42	6,06	5,80	5,62	5,47	5,35	5,26	5,18	5,11	5,00	4,92	4,80	4,73	4,64	4,56
	10	4,96	4,10	3,71	3,48	3,33	3,22	3,14	3,07	3,02	2,97	2,94	2,91	2,86	2,82	2,77	2,74	2,70	2,67	10
		10,04	7,56	6,55	5,99	5,64	5,39	5,21	5,06	4,95	4,85	4,78	4,71	4,60	4,52	4,41	4,33	4,25	4,17
	11	4,84	3,98	3,59	3,36	3,20	3,09	3,01	2,95	2,90	2,86	2,82	2,79	2,74	2,70	2,65	2,61	2,57	2,53	11
		9,85	7,20	6,22	5,67	5,32	5,07	4,88	4,74	4,63	4,54	4,46	4,40	4,29	4,21	4,10	4,02	3,94	3,86
	12	4,75	3,88	3,49	3,26	3,11	3,00	2,92	2,85	2,80	2,76	2,72	2,69	2,64	2,60	2,54	2,50	2,46	2,42	12
		9,33	6,93	5,95	5,41	5,06	4,82	4,65	4,50	4,39	4,30	4,22	4,16	4,05	3,98	3,86	3,78	3,70	3,61
	13	4,67	3,80	3,41	3,18	3,02	2,92	2,84	2,77	2,72	2,67	2,63	2,60	2,55	2,51	2,46	2,42	2,38	2,34	13
		9,07	6,70	5,74	5,20	4,86	4,62	4,44	4,30	4,19	4,10	4,02	3,96	3,85	3,78	3,67	3,59	3,51	3,42
	14	4,60	3,74	3,34	3,11	2,96	2,85	2,77	2,70	2,65	2,60	2,56	2,53	2,48	2,44	2,39	2,35	2,31	2,27	14
		8,86	6,51	5,56	5,03	4,69	4,46	4,28	4,14	4,03	3,94	3,86	3,80	3,70	3,62	3,51	3,43	3,34	3,26
	15	4,54	3,68	3,29	3,06	2,90	2,79	2,70	2,64	2,59	2,55	2,51	2,48	2,43	2,39	2,33	2,29	2,25	2,21	15
		8,68	6,36	5,42	4,89	4,56	4,32	4,14	4,00	3,89	3,80	3,73	3,67	3,56	3,48	3,36	3,29	3,20	3,12
	16	4,49	3,63	3,24	3,01	2,85	2,74	2,66	2,59	2,54	2,49	2,45	2,42	2,37	2,33	2,28	2,24	2,20	2,16	16
		8,53	6,23	5,29	4,77	4,44	4,20	4,03	3,89	3,78	3,69	3,61	3,55	3,45	3,37	3,25	3,18	3,10	3,01

---

Смотрите также файлы

• 1. Изучение и расчет параметров системы управления запасами.doc

• Игры гештальттерапии.pdf

• Практическая работа Работа с таблицами Тема Создание и форматирование таблиц в документе ms word. Цель.pdf

• орытынды аттестаттауды ткізуді лгілік аидаларын бекіту туралы.pptx

• Методические указания к лабораторной работе по дисциплине "Электроника" для студентов специальности 220100.doc