Если установлено, что серии измерений - однородные, то их можно объединить в единый массив и обрабатывать как результаты многократных равноточных измерений (п.2.2). При этом общее среднее арифметическое определяется по формуле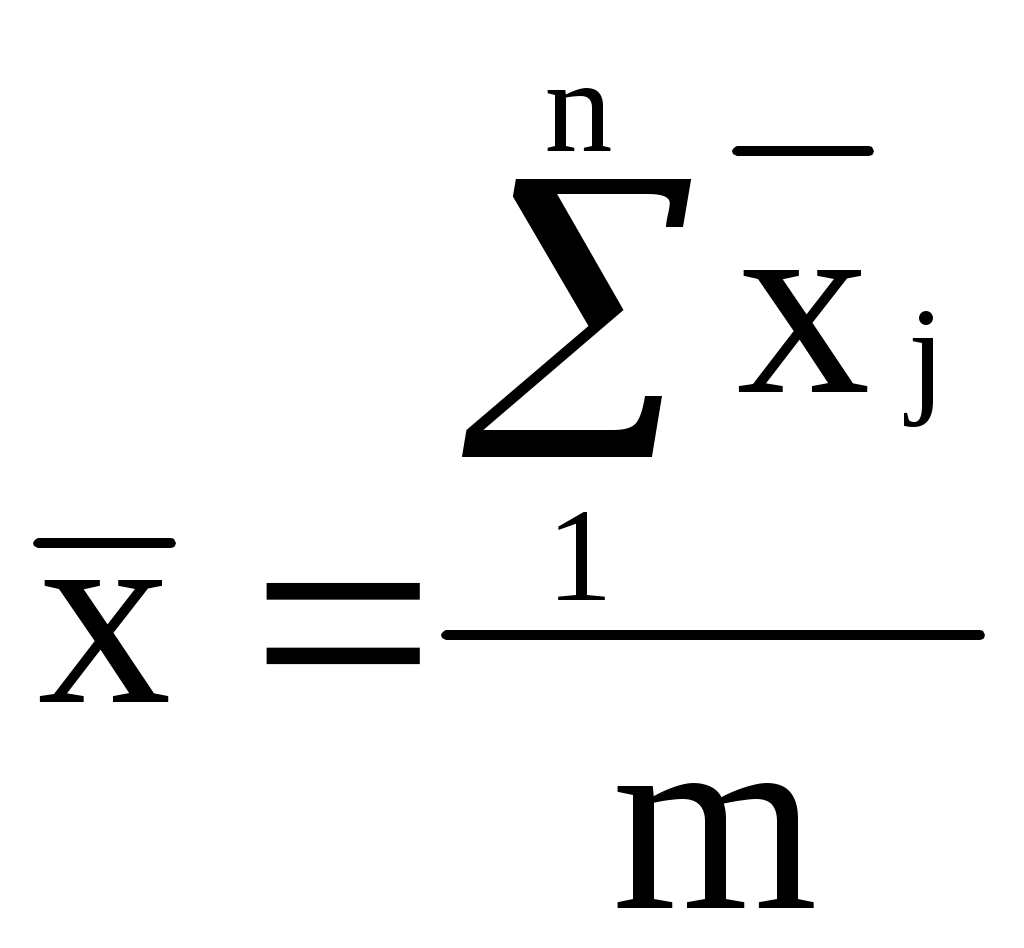, (14)где j – номер серииm – число серий.Общую дисперсии допускается определить как 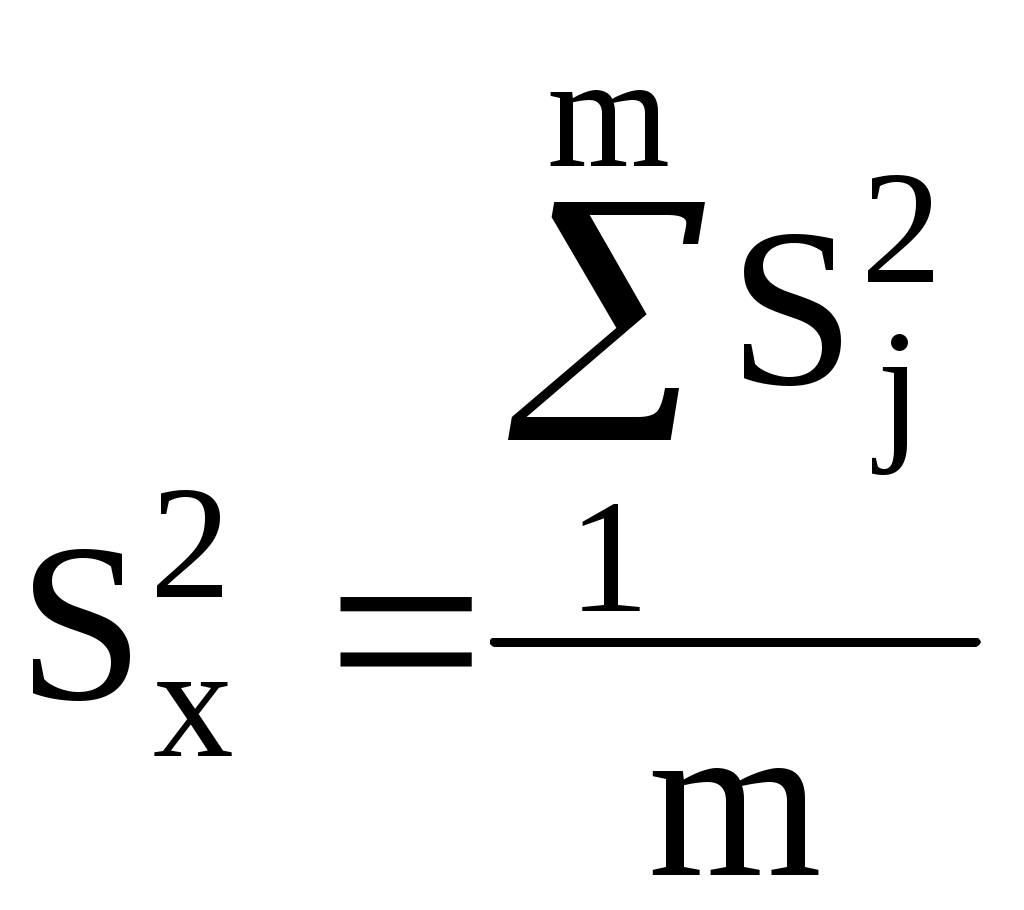(15)Где -дисперсия j-й серии.Общий результат записывается в соответствии с выражением (9) ,где ; N = n₁ + n₂ + … (16)Относительный доверительный интервал t берется из таблиц распределения Стьюдента в зависимости от числа N-1 и принятой доверительной вероятности.Если серии измерений признаны неравноточными (если условие не выполняется), то каждую группу результатов наблюдений, относящихся к одинаковым условиям (каждую серию), необходимо оценить с точки зрения степени доверия, определить их «вес», то есть степень доверия к ним в общей совокупности всех результатов, подлежащих обработке.Значение весового коэффициента g_jопределяют по следующей формуле: 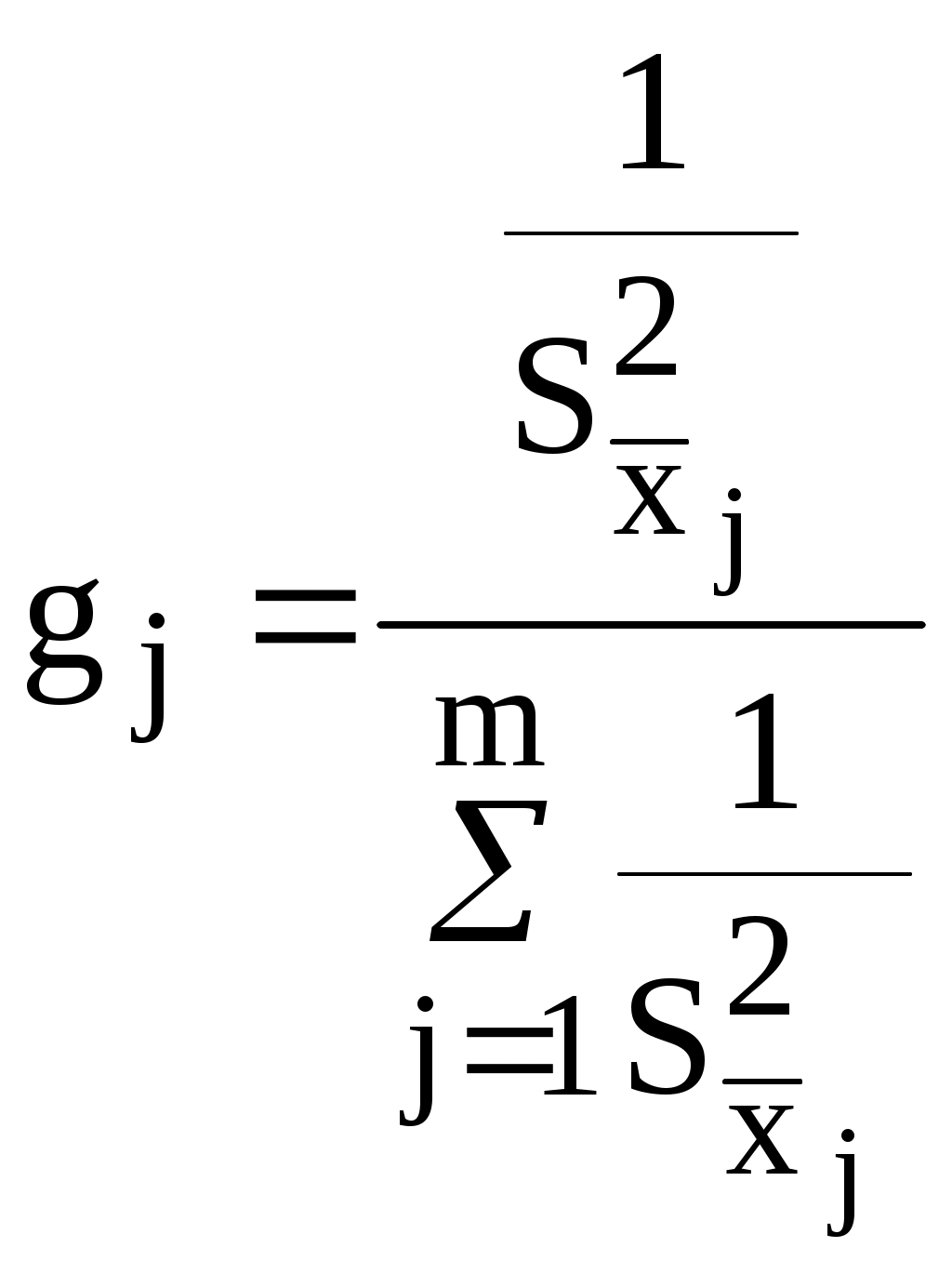(17)Среднее значение для таких серий измерений определится как среднее взвешенное: 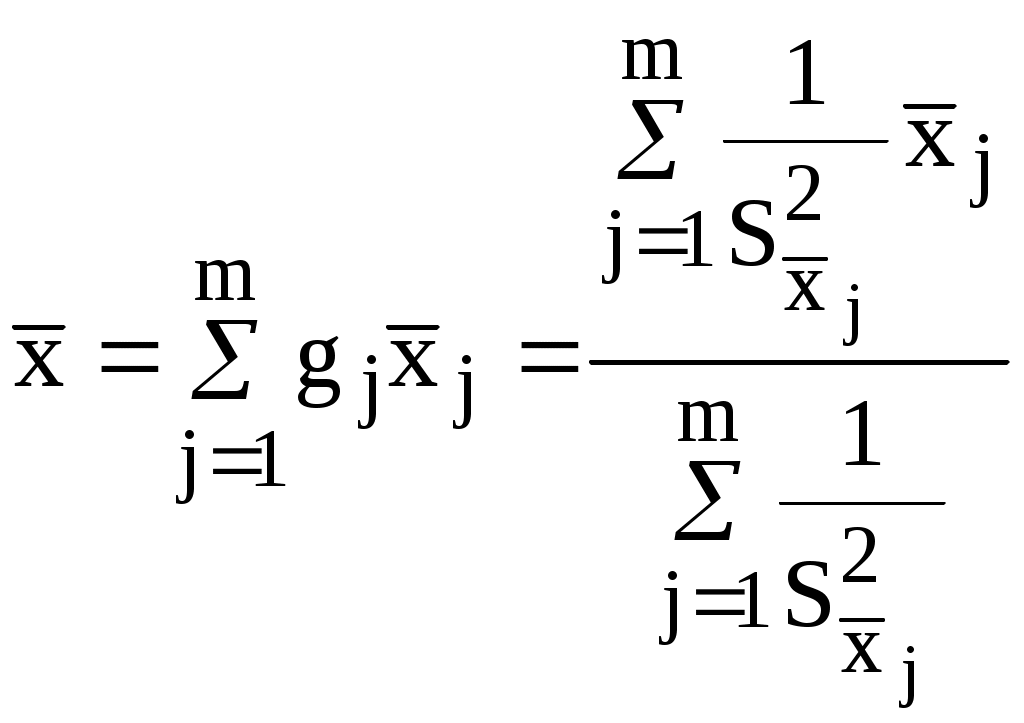(18)Оценка дисперсии рассчитывается по формуле: 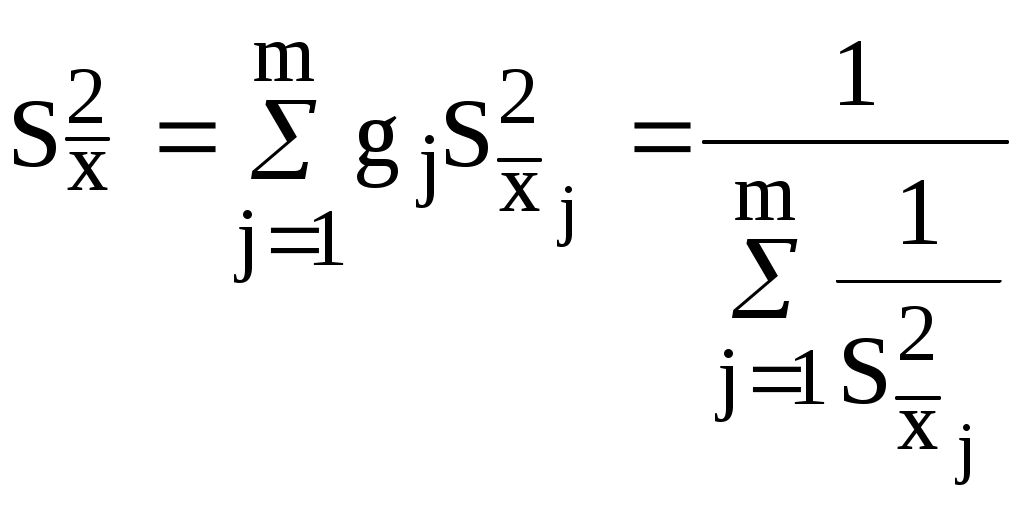(19) (20) Окончательный результат записывается в принятой форме доверительного интервала согласно выражению (9). .2.5. Описание измерительного прибора, используемого в работе

---

Рычажные скобы предназначены для точных измерений наружных линейных размеров. Измерение осуществляется путем сравнения размера контролируемого изделия с размером концевой меры длины, по которой предварительно настраивается прибор.Рычажная скоба (рис.2) снабжена тремя контактами - двумя неподвижными 1 и 2 и одним подвижным 3. Подвижный контакт, перемещаясь внутри корпуса 7, надавливает на короткое плечо рычага 4. Длинное плечо этого рычага заканчивается зубчатым сектором; сектор сцепляется с шестеренкой 5, сидящей на одной оси со стрелкой.Таким образом, перемещение подвижного контакта вызывает поворот стрелки относительно шкалы. Спиральная пружина 6 служит для создания измерительного усилия между контактом и измеряемой деталью.Для того чтобы облегчить установку скобы относительно объекта и уменьшить износ контактов, предусмотрено специальное устройство - арретир, состоящее из штифта 8 и второго рычага 9. При нажатии на штифт 8 рычаг поворачивается по часовой стрелке, надавливает на контакт 3 и отводит его от поверхности измеряемого объекта.

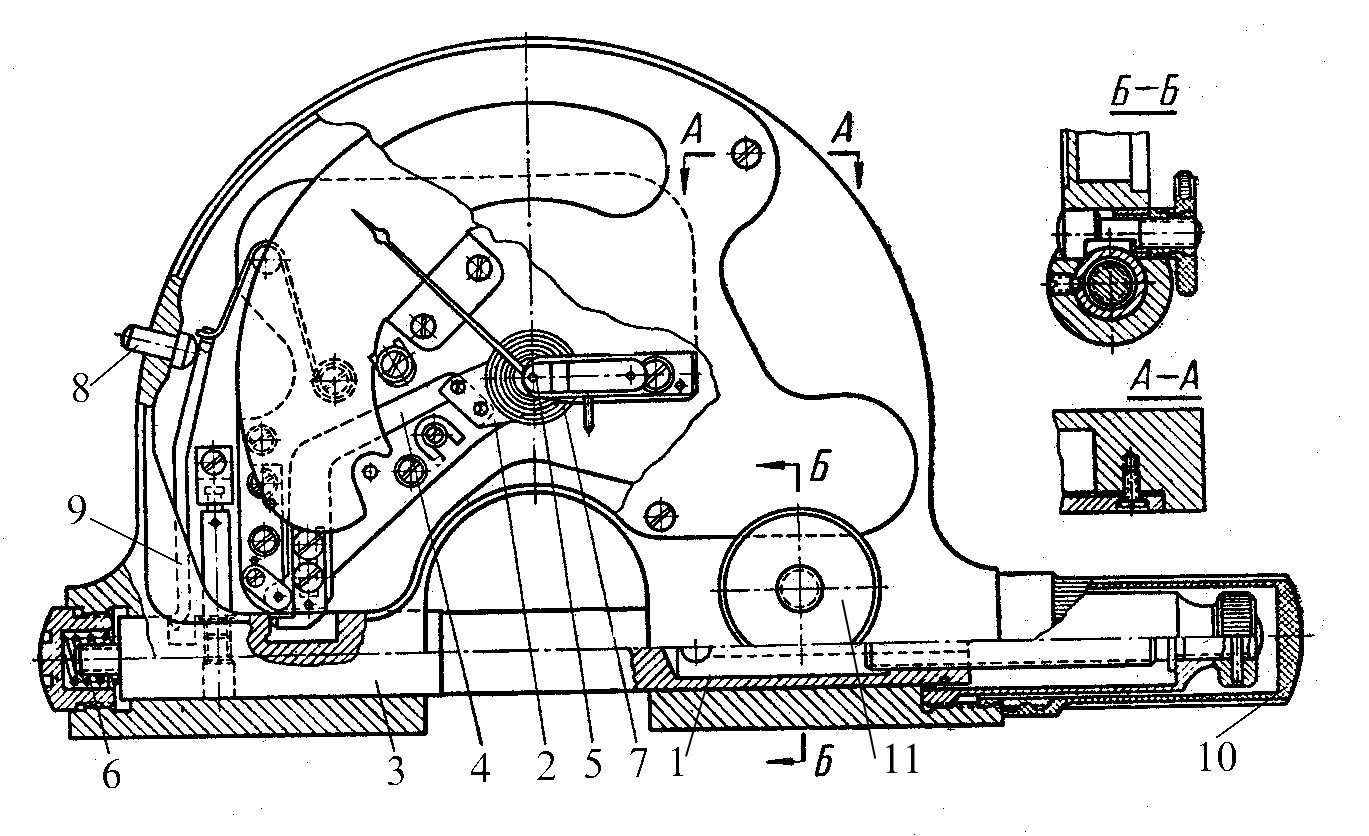Рис.2. Схема рычажной скобы.

3. Порядок проведения работы3.1. Экспериментальная часть работы состоит в выполнении многократных измерений одной и той же линейной величины несколькими наблюдателями. Измерения проводятся рычажной скобой, описанной в разделе 2.5.Настройка скобы осуществляется по концевой мере длины, соответствующей номинальному размеру проверяемого вала (для нашего примера – 25 мм). Эту концевую меру помещают между контактами 1 и 3. Отвинтив колпачок 10, вращают накатную гайку 11 до тех пор, пока стрелка прибора не станет на нулевое показание. Затем завинчивают колпачок 10, фиксируя контакт 1. Нажав на арретир 8, вынимают концевую меру длины и надвигают скобу на измеряемый вал.Результаты измерений (5...7 значений в каждой серии) заносятся в таблицу бланка отчета; причем в одну колонку записывают непосредственно показания прибора, а в другую – значения размера, вычисленные как алгебраическая сумма показаний прибора и номинального размера. 3.2. Для каждой серии измерений вычисляется среднее арифметическое

---

, стандартное отклонение и стандартное отклонение среднего с использованием формул (2), (3) и (8).

3.3. Для каждой серии измерений проверяется наличие или отсутствие грубых промахов с использованием - критерия (раздел 2.2). Если грубые промахи обнаружены, то их необходимо исключить из результатов измерений и произвести повторный расчет среднего арифметического , стандартного отклонения и стандартного отклонения среднего , а затем вновь сделать проверку на грубые промахи. Здесь, а также в других расчетах принять доверительную вероятность Р = 0,95.

3.4. С помощью критерия Фишера по формулам (12) и (13) установить однородность или неоднородность серий измерений.

3.6. Если установлено, что серии измерений - однородные равноточные, то полученные результаты объединяются в один массив, для которого выполняются расчеты по формулам (14), (15) и (16). Окончательный результат записывается в форме доверительного интервала (9).

3.7. Если установлено, что серии измерений - неравноточные, то следует рассчитать среднее взвешенное по формуле (18) и дисперсию по формуле (20), то есть с учетом весовых коэффициентов. Окончательный результат также записывается в форме доверительного интервала (9).

---

4. Контрольные вопросы4.1. Какие погрешности называют случайными?4.2. Что такое закон распределения вероятности случайной величины?4.3. Что такое математическое ожидание случайной величины?4.4. Что характеризует дисперсия случайной величины? Как связаны между собой дисперсия и среднее квадратическое отклонение?4.5. Что такое доверительный интервал? Доверительная вероятность?4.6. Как производится проверка результатов многократных измерений на предмет обнаружения грубых промахов?4.7. Что такое равноточные и неравноточные серии измерений?4.8. Как проверяется однородность (равноточность) серий измерений с помощью критерия Фишера?4.9. Что такое весовые коэффициенты?

5. 
   Библиографический список
   

5.1. Бурдун Г.Д., Марков Б.Н. Основы метрологии: Учебн. пособие. - 3-е изд. перераб. и доп. - М.: Изд-во стандартов, 1985.5.2. Шишкин И.Ф. Основы метрологии, стандартизации и контроля качества: Учебн. пособие. - М.: Изд-во стандартов, 1988.5.3. Димов Ю.В. Метрология, стандартизация и сертификация. - СПб.: Питер, 20065.4. Фрумкин В.Д., Рубичев Н.А. Теория вероятностей в метрологии и измерительной технике. - М.: Машиностроение, 1987.5.5. Кузнецов В.А., Ялунина Г.В. Метрология (теоретические, прикладные и законодательные основы). Общая метрология: Учеб.пособие.-М.: ИПК Издательство стандартов, 2001.- 336с.

Кафедра ИМС Лаборатория линейных и угловых измерений

ОБРАБОТКА РЕЗУЛЬТАТОВ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ ПРИМЕР ОФОРМЛЕНИЯ РАБОТЫ

Работа № М1

Задание.	Выполнить многократные измерения одной и той же линейной величины несколькими наблюдателями. Результаты измерений занести в таблицу бланка расчета. Произвести обработку результатов многократных измерений.
	Исходные данные d=____25 мм_______; n=___6_________; P=____0.95________рррроол

1. Результаты, полученные при многократных измерениях диаметра вала, мм. Табл. 1

---

№ п/п	I серия		II серия
1	-0,042	24,958	-0,038	24,962
2	-0.044	24,956	-0,049	24,951
3	-0,035	24.965	-0,043	24,957
4	-0,038	24.962	-0,035	24,965
5	-0,038	24,962	-0,034	24,966
6	-0,040	24,960	-0,040	24,960

2. Определим основные характеристики случайной величины.Табл. 2

Параметр	I серия	II серия
1. Среднее арифметическое	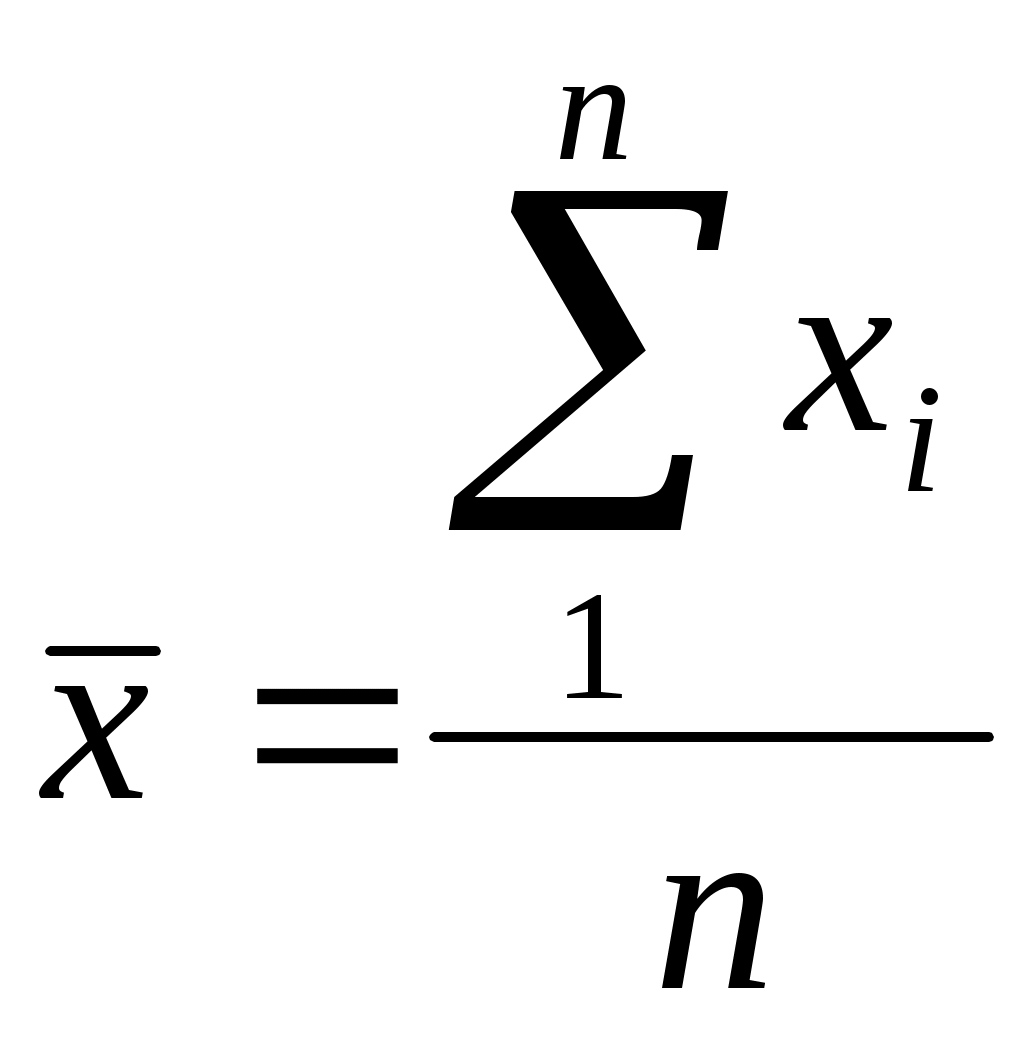24,961	24,960
2. Стандартное отклонение	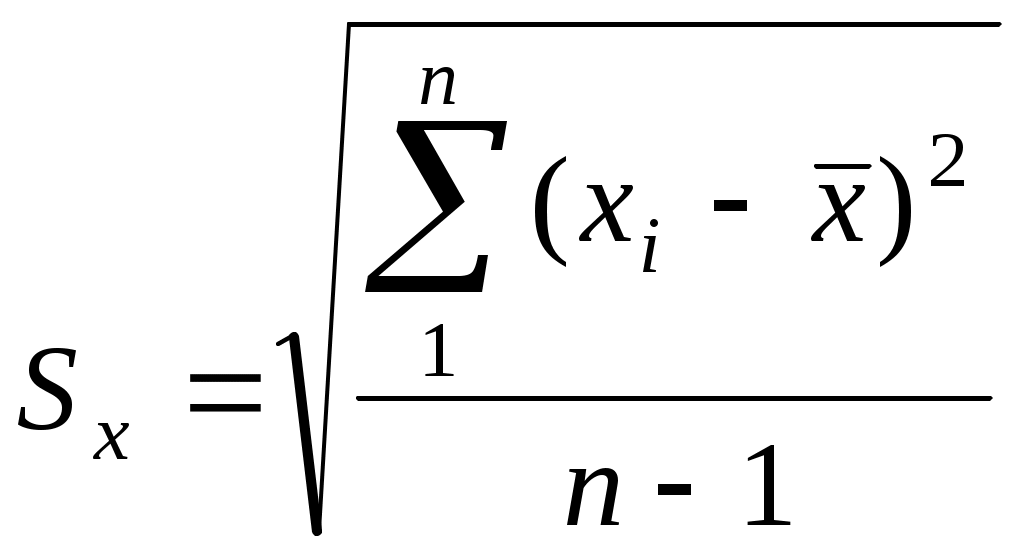0,0033	0,0056
3. Стандартное отклонение средних	0,0013	0,0023

3. Произведем проверку отсутствия грубых промахов в каждой серии с использованием - критерия:для первой серии , ; для второй серии , .

---

Смотрите также файлы

• 1. Изучение и расчет параметров системы управления запасами.doc

• Игры гештальттерапии.pdf

• Практическая работа Работа с таблицами Тема Создание и форматирование таблиц в документе ms word. Цель.pdf

• орытынды аттестаттауды ткізуді лгілік аидаларын бекіту туралы.pptx

• Методические указания к лабораторной работе по дисциплине "Электроника" для студентов специальности 220100.doc