Файл: Практическое занятие 1 Обработка результатов прямых измерений. Однократные измерения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 581
Скачиваний: 13
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Обработка результатов прямых измерений. Однократные измерения.
Обработка результатов прямых измерений. Округление данных.
Обработка результатов прямых многократных измерений.
Обработка результатов косвенных измерений
Обработка результатов активного эксперимента в динамическом режиме
Интерпретация результатов эксперимента. Приближение табличных данных функцией.
Планирование эксперимента и статистическая обработка его результатов
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1
Обработка результатов прямых измерений. Однократные измерения.
Температура в термостате измеряется техническим прибором со шкалой NK
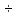 NH, имеющим класс точности К. Показания прибора X. Определить допускаемую погрешность измерения, записать результат в общепринятом виде.
NH, имеющим класс точности К. Показания прибора X. Определить допускаемую погрешность измерения, записать результат в общепринятом виде.Исходные данные
| Вариант | NK 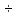 NH NH | К | X |
| 6 | -100 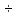 +250,°C +250,°C | 1,0 | -85, °C |
Решение:
Т.к. класс точности равен 1, то допускаемая относительная погрешность измерения равна: 1 %.
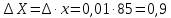 .
.Результат измерения:
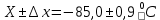 .
.ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2
Обработка результатов прямых измерений. Округление данных.
Результаты измерений записаны следующим образом: погрешность
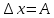 , результат х = В. Округлить результат до N значащих цифр и записать в общепринятом виде.
, результат х = В. Округлить результат до N значащих цифр и записать в общепринятом виде.| Вариант | А | В | N |
| 6 | 0,075 | 20,749 | 1 |
Решение:
Округлим результат до одной значащей цифры: х = 20,749
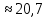 .
.Тогда:
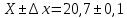 .
.ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3
Обработка результатов прямых многократных измерений.
В теплофизическом эксперименте проведен ряд измерений, представленный в таблице. Требуется определить среднее арифметическое ряда измерений, оценку средней квадратической погрешности ряда измерений, полуширину доверительного интервала при заданной доверительной вероятности. Записать результат в общепринятом виде.
| Вариант | Довер, вер-ть Р | n | Отдельные значения ряда, / | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 6 | 0,9 | 9 | 3,95 | 3,97 | 3,99 | 3,90 | 3,93 | 3,94 | 3,93 | 3,91 | 3,94 | |
Распределение Стьюдента tpn.
| n | р | |||||
| 0,5 | 0,6 | 0,7 | 0,9 | 0,95 | 0,999 | |
| 9 | 0,71 | 0,88 | 1,1 | 1,9 | 2.3 | 5,0 |
Решение:
Среднее арифметическое значение результатов ряда наблюдений:
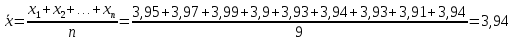 .
.Вычисляется значение средней квадратичной ошибки отдельного результата измерений:
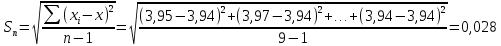 .
.Значение средней квадратичной ошибки среднего арифметического определяется из формулы:
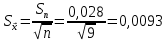 .
.Абсолютная погрешность результата измерений
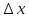 определяется умножением средней квадратичной погрешности среднего арифметического на коэффициент (коэффициент Стьюдента), зависящий от числа произведенных измерений и выбранной доверительной вероятности
определяется умножением средней квадратичной погрешности среднего арифметического на коэффициент (коэффициент Стьюдента), зависящий от числа произведенных измерений и выбранной доверительной вероятности 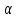
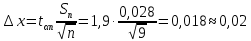 .
.Доверительный интервал, в котором содержится истинное значение искомой величины хист, с заданной вероятностью определится границами
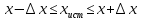 .
.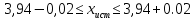 ,
, 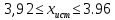
Окончательный результат записывается в виде:
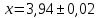 .
.ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4
Обработка результатов косвенных измерений
Результат косвенного измерения определяется по приведенной формуле. Погрешности прямых измерений и средние значения параметров приведены в таблице. Записать формулу для определения погрешности (абсолютной для четного или относительной для нечетного варианта) косвенного измерения, рассчитать ее для средних значений прямых измерений с указанием размерности.
| Вариант | Формула | Погрешности прямых измерений | Средние значения параметров | ||
| 6 | 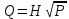 | 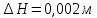 | 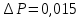 | 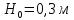 | 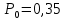 |
Решение:
Погрешность определения каждого аргумента Xj приводит к появлению составляющей погрешности
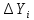 величины Y.
величины Y.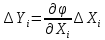 .
.Тогда:
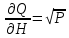 , :
, : 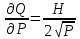 .
.Абсолөтнаә погрешностғ косвенного измерения:
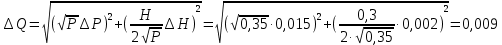 м.
м.ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5
Обработка результатов активного эксперимента в динамическом режиме
В процессе активного эксперимента определена динамическая характеристика - переходная функция объекта как реакция выходной величины на скачкообразное воздействие (см. рис.). Нарисовать переходную функцию в реальных координатах согласно заданию. Графически определить время запаздывания и постоянную времени объекта.
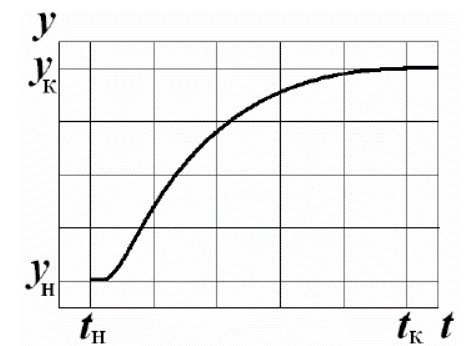
| Вариант | yн | yк | tн, с | tк, с |
| 6 | 1,0 | 2,0 | 200 | 2200 |
Решение:
Переходная функция в реальных координатах:
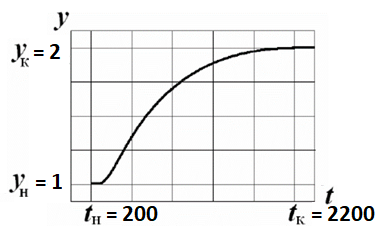
Построим касательную к функции в точке перегиба и укажем на графике постоянную времени и время запаздывания.
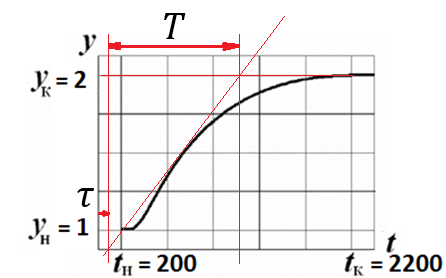
Из графика определяем:
Время запаздывания:
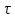 = 86 с, постоянная времени: T = 1154 c.
= 86 с, постоянная времени: T = 1154 c.ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6
Интерпретация результатов эксперимента. Приближение табличных данных функцией.
Расходомер с электрическим аналоговым выходным сигналом работает в составе АСЭИ. Согласно градуировке расходомера получена таблица соответствия выходного сигнала прибора X, мА фактическим расходам Q, л/мин. В подсистеме первичной обработки информации для процедуры преобразования данных в конкретную физическую величину необходима эмпирическая формула. Предложить простую двухпараметрическую эмпирическую формулу (выбрать из линейной, степенной или экспоненциальной функций) по методу наименьших квадратичных ошибок. В качестве критерия приближения использовать максимум коэффициента корреляции R. Результаты представить в виде графика.
Линейная функция у=ах+b,
Степенная функция у=ахb;
Экспоненциальная функция у=аехр(bх) =аеbx.
| Вариант | Данные | ||||||||||
| 6 | Х, мА | 4,0 | 5,7 | 8,0 | 10,0 | 12,0 | - | - | 18,6 | 20 | |
| Q, л/мин | 0,23 | 28 | 46 | 80 | 128 | - | - | 245 | 250 | | |
Решение:
Выбираем эмпирическую формулу – линейную у=ах+b
Расчетные формулы для определения коэффициентов a,b методом наименьших квадратов имеют вид:
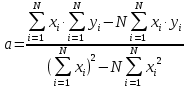 ,
, 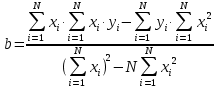
Построим корреляционное поле данных X-Q:
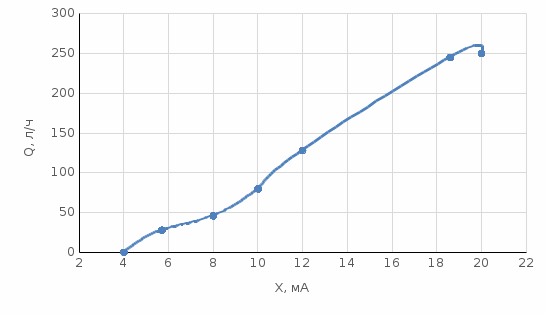
Для удобства Q обозначим через Y.
Для определения необходимых для расчета суммарных значений составим расчетную таблицу:
| i | Xi | Yi | Xi2 | Yi2 | Xi*Yi |
| 1 | 4 | 0,23 | 16 | 0,0529 | 0,92 |
| 2 | 5,7 | 28 | 32,49 | 784 | 159,6 |
| 3 | 8 | 46 | 64 | 2116 | 368 |
| 4 | 10 | 80 | 100 | 6400 | 800 |
| 5 | 12 | 128 | 144 | 16384 | 1536 |
| 6 | 18,6 | 245 | 345,96 | 60025 | 4557 |
| 7 | 20 | 250 | 400 | 62500 | 5000 |
| ∑ | 78,3 | 777,23 | 1102,5 | 148209 | 12422 |
Вычислим коэффициенты:
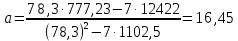 ,
, 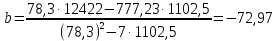 .
.Эмпирическое уравнение имеет вид: