Файл: Задача 10 Цепь, состоящая из пяти резисторов, присоединена к источнику электрической энергии, напряжение на зажимах которого U.docx
Добавлен: 10.11.2023
Просмотров: 386
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача № 10
Цепь, состоящая из пяти резисторов, присоединена к источнику электрической энергии, напряжение на зажимах которого UАВ(Рис.1). Токи в резисторах соответственно равны I1, I2, I3, I4, I5.Определить величины, отмеченные знаками вопроса в табл. 2.
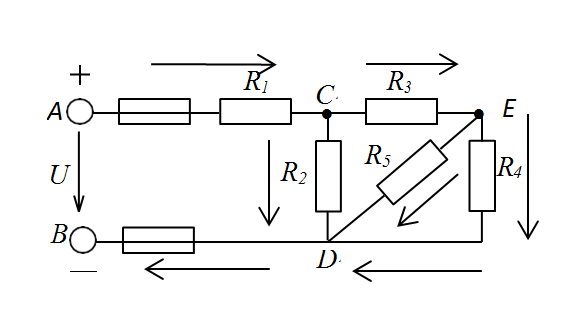
Рисунок 1
Решение
-
Делаем краткую запись условия задачи.
Дано: UAB = 100 В, R2 = 10 Ом, R5 = 20 Ом, I2 = 6 A, I4 = 1,6 A, I5 = 2,4 A.
Определить: UCD, RAB, RCD, R1, R3, R4, I1, I3.
-
Обозначим стрелками токи, протекающие в каждом резисторе с учетом их направления, узлы цепи буквами A, B, C, D. -
Сопротивления R4, R5 соединены параллельно.
Найдем общее сопротивление при таком соединении:
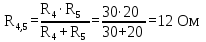
-
Найдем падение напряжения на резисторе R5. И т.к. резисторы R4 и R5 соединены параллельно, то U5=U4:
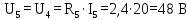
-
Найдем ток I4,5, проходящий через резисторы R4 и R5. И т.к. ток при последовательном соединении одинаков, то I4,5 = I3: -
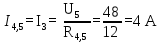
-
Найдем падение напряжения на резисторе R2. И т.к. при параллельном соединении падение напряжения на элементах равны, то U2=U3(4,5)=UCD
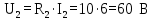
-
Составим уравнение суммы падения напряжений на резисторах R3, R4,5 и найдем из него сопротивление резистора R3:
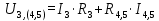
Тогда
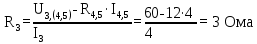
-
При последовательном соединении элементов падение напряжения на всех элементах цепи равняется сумме падений напряжения на каждом элементе. Найдем падение напряжения на резисторе U1:
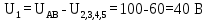
-
Найдем ток участка цепи ICD. Т.к. резисторы R2 и группа резисторов R3,(4,5) соединены параллельно и при последовательном соединении токи элементов цепи равны между собой, то:
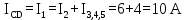
-
Найдем сопротивление резистора R1:
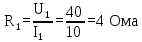
-
Найдем общее сопротивление цепи:
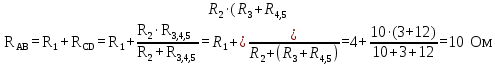
-
Тогда сопротивление на участке цепи CD равно:
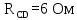
Задача № 13
На рис. 2 изображена схема воздушной линии электропередачи к потре- бителю мощностью Р2и напряжением потребителя U2; длина линии l.
Определить ток в линии I и площадь поперечного сечения S проводов ли- нии, если известна допустимая относительная потеря напряжения в линии е, материал и удельная проводимость ɣ проводов линии.
Определить сопротивление проводов линии RПР, абсолютную потерю напряжения ∆U, потерю мощности ∆Р в линии и коэффициент полезного дей- ствия линии η.
Числовые значения исходных величин указаны в табл. 3
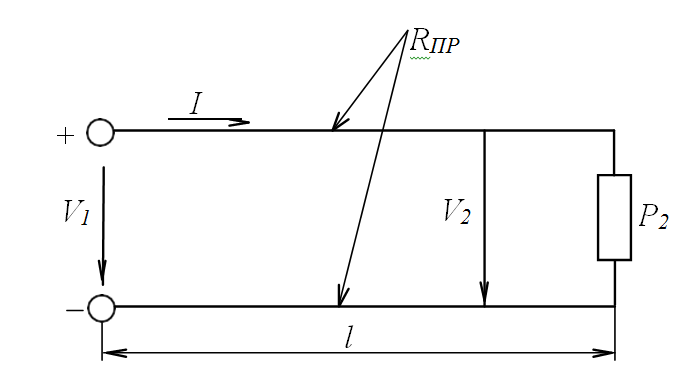
Рисунок 2
Решение
-
Делаем краткую запись условия задачи.
Дано: P2 = 15,2 кВТ, U2 = 380 В, l = 400 м, ɣ = 34,5
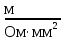 , е = 5 %.
, е = 5 %.Определить: RПР, ∆U, ∆Р, η.
-
Ток в линии электропередачи:
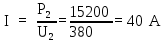
-
Площадь поперечного сечения проводов линии: -
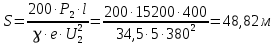 Выбираем ближайшее большее стандартное сечение SСТ = 50 мм2. Сопротивление проводов линии:
Выбираем ближайшее большее стандартное сечение SСТ = 50 мм2. Сопротивление проводов линии:
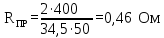
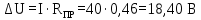
-
Потеря мощности в линии ∆Р:

-
Напряжение в начале линии:
U1 = U2 + ∆U = 380 + 18,4 = 398,4 В
-
КПД линии:
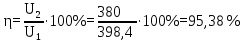
Задача № 29
По проводу длиной l = 60 см, находящемуся в однородном магнитном поле с индукцией В = 1,2 Тл и расположенному в плоскости
, перпендикулярной направлению поля, протекает ток I от источника питания с напряжением U= 7В. На провод действует электромагнитная сила FЭМ, перемещающая его со скоростью V = 8 м/с. Сопротивление провода с подводящими проводами R= 0,5 Ом.
Определить значение тока I0 при неподвижном проводе, противо-ЭДС, наведенную в проводе, и ток I при его перемещении.
Решение
-
Делаем краткую запись условия задачи.
Дано: l = 60 см, В = 1,2 Тл, U = 7 В, ν = 8 м/с, R = 0,5 Ом.
Определить: I0, противо-ЭДС, I.
-
Ток протекает от положительного полюса источника к отрицательному. Под действием электромагнитной силы проводник будет перемещаться влево (правило левой руки). В проводнике будет наводиться ЭДС (явление электромагнитной индукции), равная:
E = B · I · V = 1,2 · 0,6 · 8 = 5,76 В
Направление ЭДС определим по правилу правой руки. Оно противопо- ложно направлению ЭДС внешнего источника и тока, поэтому эта ЭДС (в элек- тродвигателях) называется противо-ЭДС.
-
Ток в проводнике:
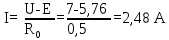
-
При остановке проводника E исчезает, поэтому сила тока при неподвижном проводнике будет равна:
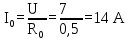
Задача № 33
В сеть переменного тока частотой f = 50 Гц включена катушка индуктивности. Полная мощность цепи S = 625 ВА, коэффициент мощности cosφ = 0,6; показание амперметра I = 5 А. Определить активное R, индуктивное ХL и полное Z сопротивления; показания вольтметра и ваттметра, включенных в цепь.
Начертить схему цепи и построить векторную диаграмму тока и напряжений в масштабе mu = 22 В/см. Пояснить построение диаграммы.
Решение
-
Делаем краткую запись условия задачи.
Дано: f = 50 Гц, S = 625 ВА, cosφ= 0,6, I = 5 А.
Определить: R, ХL, Z, V, P.
-
Коэффициент мощности — это отношение активной мощности к полной. Отсюда активная мощность:
P=S·cosφ=625·0,6 =375 Вт (и это показания ваттметра)
-
Амперметр показывает полный ток. Т.к.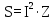 , то полное сопротивление равно:
, то полное сопротивление равно:
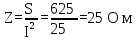
-
Мощность прямо пропорциональна сопротивлению, тогда найдем активное сопротивление:
R = Z
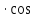 φ=25
φ=25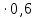 =15 Ом
=15 Ом-
Найдем реактивное сопротивление:
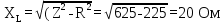
-
Вольтметр покажет падение напряжения на катушке, найдем через мощность. Т.к. S = U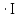 , тогда:
, тогда:
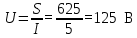
-
Начертим схему. Катушка имеет активную и реактивную составляющие сопротивления, тогда:
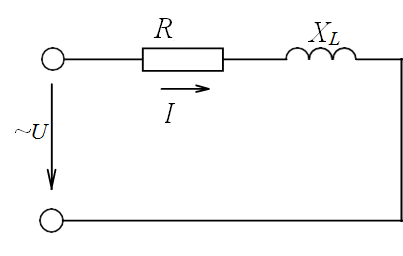
Рисунок 3
-
Падение напряжения на R и XL будут равны:
UR =I
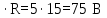 ,
,UL=I
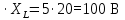
-
Построим векторную диаграмму тока и напряжений. Примем следующий масштаб: mu = 22 В/см, mI=2,5A/см:
а) Катушка носит индуктивный характер, а значит, в ней напряжение опережает ток по фазе на 90°.
б) Резистор обладает только активным сопротивлением, и напряжение в нем совпадает по фазе с током.
в) для начала отложим вектор тока в масштабе:
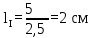
г) далее, отложим вектор напряжения на катушке. Получается, что нужно отложить вверх, так как напряжение в катушке опережает ток.
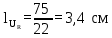
д) теперь мы будем откладывать вектор активного сопротивления, так как напряжение в одной фазе с током, то мы его откладываем из конца вектора UL параллельно вектору тока I.
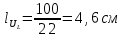

UR





UL
U

I

Рисунок 4
Задача № 43
В сеть переменного тока частотой f = 50 Гц последовательно включены резистор R и конденсатор c емкостным сопротивлением ХС, величины которых приведены в табл. 4. Кроме того, известна одна из дополнительных величин (I, P, Q).
Начертить схему цепи и определить следующие величины:
-
полное сопротивление цепи Z; -
напряжение U, приложенное к цепи; -
силу тока в цепи I; -
коэффициент мощности цепи cosφ; -
активную P, реактивную Q и полную S мощности, потребляемые цепью.
Начертить в масштабе векторную диаграмму цепи и пояснить ее построение.
Решение
-
Делаем краткую запись условия задачи.
Дано: f = 50 Гц, R=16 Ом, XC=12 Ом, Q=-48 Вар.
Определить: Z, U, I, cosφ, P, Q, S.


R
C
-
Начертим схему.






Рисунок 5
-
Из формулы для емкостного сопротивления проводника найдем емкость конденсатора:
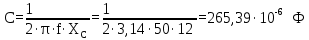
-
Из формулы реактивной мощности для конденсатора найдем падение напряжения на нем:
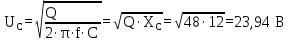
-
Найдем полное сопротивление цепи:
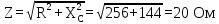
-
Найдем ток в цепи. Т.к. при последовательном соединении элементов цепи общий ток в ней равен току на каждом из элементов цепи, то:
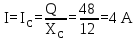
-
Найдем напряжение U, приложенное к цепи: