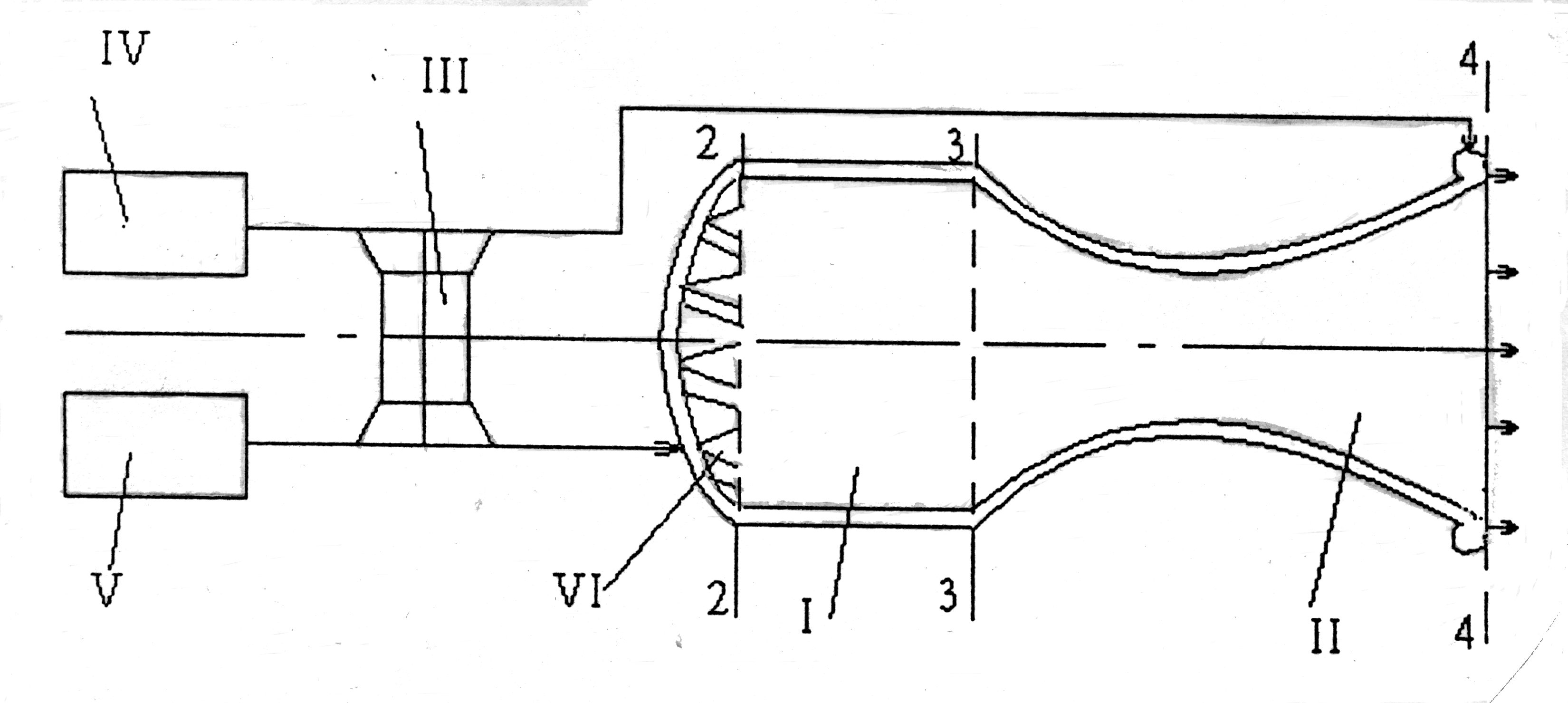
Рассмотрим ЖРД, работающий на газообразных компонентах топлива. Горючее – углеводородное топливо, окислитель – смесь кислорода и азота, заданная молярными долями ( и ). Горючее и окислитель впрыскиваются в камеру сгорания ЖРД через форсунки VI и определяют состав смеси газов в сечении 2-2 камеры сгорания. Термодинамические параметры в сечениях 2-2 - вход в камеру сгорания, 3-3 – вход в сопло, 4-4 - срез сопла соответствуют термодинамическим параметрам в точках 2, 3 и 4 разомкнутого цикла ЖРД, процессы которого в координатах pV и TS имеют следующий вид:

Процесс 2-3 изобарно – адиабатно - изоэнтальпийный процесс (dp=0, Q=0, dH=0)сгорания топлива в камере сгорания двигателя. Процесс 3-4 – адиабатно - изоэнтропийный процесс (Q=0, dS=0) истечения продуктов сгорания из сопла в среду с заданным давлением, причем давление на срезе сопла в сечении 4-4 равно давлению окружающей среды, т.е. сопло – расчетное.

Для определения термодинамических характеристик в сечениях 2-2, 3-3, 4-4 двигателя исходными данными являются: относительное давление в камере сгорания - =101325 Па, давление на срезе сопла p₄, которое равно давлению среды – p_у на заданной высоте «у» полета (p₄=p_у), а также природа топлива, которая характеризуется заданным элементным химическим составом и энтальпией, определяемой по справочным материалам. Элементный химический состав определяет возможный состав индивидуальных веществ, образующих продукты сгорания. Рабочее тело (топливо и продукты сгорания) рассматривается как смесь идеальных газов в расчетных сечениях двигателя. Эта многокомпонентная смесь индивидуальных веществ в газообразном состоянии является простой закрытой термодинамической системой, состояние которой задается двумя независимыми параметрами: p и Н (для камеры сгорания) и p и S (для сопла).Кроме давлений и p₄ , заданными величинами являются также коэффициент избытка окислителя _ок и температура топлива в сечении 2-2, равная Т₂=298,15К.

Задачей термодинамического расчета ракетного двигателя в условиях термодинамического равновесия реагирующих систем в характерных сечениях двигателя является определение химического состава продуктов сгорания и температуры, а также интегральных и дифференциальных свойств системы в этих сечениях ЖРД.

В рассматриваемой задаче принятые модели рабочего тела и процессов позволяют провести расчет равновесных состояний системы при известных параметрах: давлении и энтальпии – для выходного сечения камеры сгорания двигателя (3 – 3), давлении и энтропии – для выходного сечения сопла на расчетном режиме его работы (4-4). Эти параметры однозначно характеризуют рассматриваемые случаи установления равновесия системы и полностью определяют ее термодинамическое состояние. При известных параметрах состояния химический состав продуктов сгорания в условиях равновесия определяется исходным элементным составом топлива и не зависит от пути процесса, по которому было достигнуто то или иное термодинамическое состояние. Поэтому для определения характерных параметров процесса достаточно знать только параметры в начальной и в конечной точке процесса. При этом детальных сведений о геометрии и конструкции элементов двигателя не требуется.

---

Цель термодинамического расчета ракетного двигателя в общем случае является определение параметров потока: температуры, давления, скорости, термодинамических и теплофизических свойств рабочего тела и его химического состава, необходимых для определения скорости истечения (удельной тяги), секундного массового расхода топлива и характерных размеров камеры сгорания, сопла и других агрегатов двигателя, а также для расчета газодинамических процессов и процессов теплообмена.

В данном разделе результаты термодинамического расчета и определения интегральных и дифференциальных параметров используются для расчета скорости истечения рабочего тела из сопла, которая равна на расчетном режиме работы сопла удельному импульсу тяги I_y (I_y=W_c) , а также тяги двигателя P= W_c и числа Маха , где _т секундный массовый расход рабочего тела (величина заданная).

В сечении 2-2 камеры сгорания расчет термодинамических параметров проводится для смеси нереагируюших газов известного состава при заданных параметрах: давлении и температуре. Этот состав смеси газов является исходным элементным составом топлива для расчета состава продуктов сгорания в условиях равновесия в сечении 3-3 камеры сгорания.

Методика и порядок расчета ЖРД с учетом одной химической реакции

Определение соотношения компонентов в топливе.

Для определения состава системы при химической реакции сгорания топлива записывается уравнение химической реакции, которое для произвольной реакции в условной форме имеет вид:

, или (1)

где и - стехиометрические коэффициенты компонентов реакции. Для левой части уравнения (исходных веществ) они отрицательны, а для правой (продуктов реакции) – положительны.

Например, для химической реакции 2CH+ O₂=2CO₂+H₂O имеем:

, ,

или 2CO₂+1H₂O-2CH- O₂-0N₂=0 ,

где , , , .

Задается число молей кислорода, например:

Определяется число молей азота, который впрыскивается через форсунки в камеру сгорания ЖРД в смеси с кислородом при заданных молярных долях и :

. (2)

При , и 3,7619 моль.

Азот не участвует в реакции, но его присутствие влияет на ход реакции. Он включен в уравнение химической реакции формально, полагая, что стехиометрический коэффициент .

Определяется число молей горючего. Обычно в ЖРД используют ракетное топливо с недостатком окислителя по сравнению со стехиометрическим составом. Это отличие стехиометрического соотношения компонентов от действительного характеризуется коэффициентом избытка окислителя (Обычно для ЖРД _ок1). Тогда

. (3)

Для приведенного примера при =0,8

моль.

Определяется число молей смеси газов исходного состава, которое впрыскивается в камеру сгорания через форсунки:

n=n_i (4)

Для приведенного примера n=n₀+ n+ n_Г=1+3,7619+1=5,7619 моль.

Определяются мольные доли смеси: x_i=

Например: x x, x_г= , х_i=1.

---

Определяется масса смеси газов

m=m_i , (5)

где m_i=n_i; -молярные массы компонентов смеси, которые определяются при известных относительных молекулярных массах M_i, взятых из таблиц индивидуальных веществ по формуле:

=М_i^, . (6)

например: , , ,

m, m, m_г=n_гг .

Определяются массовые доли смеси газов _i=, _i=1.

Например: , , _г= .

Расчет параметров, характеризующих интегральные свойства системы в сечении 2-2 камеры сгорания ЖРД.

Определяется молярная масса смеси газов

, . (7)

Определяется объем смеси газов

V=, м³ , (8)

где молярная газовая постоянная, Т – температура. В сечении 2-2 температура задана и равна Т₂ = 298,15К, р - давление в камере сгорания p==101325 Па, где - заданная величина.

Определяется плотность смеси газов

(9)

Определяется удельная газовая постоянная смеси газов

R= (10)

Определяется энтальпия смеси индивидуальных веществ

H= (11)

где -молярная энтальпия i-го вещества.

= ),

где - энтальпия образования i- го индивидуального вещества при Т₀=0К, - избыточная энтальпия при нагреве вещества от Т₀ до температуры Т. и -определяются из таблиц индивидуальных веществ.

Определяется энтропия смеси газов

S= (12)

=  ,

где - молярная энтропия, которая зависит от температуры и давления; = -парциальное давление i-ой компоненты смеси газов, отнесенное к давлению в одну физическую атмосферу p⁰=101325Па; - относительное давление смеси газов в камере сгорания ЖРД (величина заданная); - молярная энтропия i-го вещества при давлении р⁰=101325Па (берется из таблиц индивидуальных веществ).

Расчет параметров, характеризующих дифференциальные свойства системы в сечении 2-2 камеры сгорания ЖРД.

Определяется изобарная теплоемкость смеси газа

= , , (13)

где , - молярная изобарная теплоемкость i-го компонента смеси берется из таблиц справочника.

По уравнению Майера определяется изохорная теплоемкость смеси газов

C_v=C_p- n, . (14)

Определяется показатель адиабаты смеси газов

к= (15)

Определяется скорость звука

(16)

Расчет параметров химически реагирующей смеси газов в сечении 3-3 камеры сгорания ЖРД.

Процесс сгорания топлива в камере сгорания ЖРД (2-3) является изобарно-адиабатно-изоэнтальпийным (dp=), так как теплота извне к системе не подводится и согласно уравнению 1-го закона термодинамики для простой закрытой системы dН=, т.е. энтальпия в сечении 3-3 камеры сгорания должна быть равна энтальпии в сечении 2-2: Н₃=Н₂.

Увеличение температуры рабочего тепла в камере сгорания двигателя происходит за счет выделения тепловой энергии при протекании химической реакции сгорания топлива. При этом задача определения температуры на выходе из камеры сгорания – Т₃ и химического состава продуктов сгорания сводится к расчету равновесного состояния системы в сечении 3-3 при двух фиксированных параметрах: давлении (р₃=р₂) и энтальпии (Н₃₌Н₂).

---

В соответствии со 2-м законом термодинамики энтропия системы будет возрастать из-за необратимого протекания процесса сгорания топлива и при достижении состояния равновесия примет значение, соответствующее максимуму энтропии. Таким образом, процесс сгорания в камере сгорания ЖРД соответствует переходу системы из химически неравновесного в равновесное состояние, которое полностью определяется заданием двух независимых термодинамических параметров (в данном случае: p=const и H=const).

Состав реагирующей смеси газов в начальный момент химической реакции определяется числами молей веществ, впрыскиваемых в камеру сгорания через форсунки, - ,моль.

Например, для реакции:

2CH+ O₂=2CO₂+H₂O ,

,

,

.

Текущие значения количеств веществ для термодинамической системы с учетом одной химической реакции определяются соотношением , где - количество i-ой компоненты смеси в начальный момент реакции;  - величина пробега химической реакции, которая полностью характеризует в этом случае степень изменения состава системы при химической реакции. Она показывает, насколько сдвинулась реакция по отношению к начальному состоянию термодинамической системы. Неизвестная величина  при переходе системы в равновесное состояние определяется из условия равенства нулю сродства химической реакции А, которое при сопряжении термодинамической системы с окружающей средой р, Т=const имеет вид:

, или dG_p,T=0.

При А=О достигается состояние равновесия системы. При этом свободная энергия Гиббса G=G( принимает минимальное значение, а пробег химической реакции *_рав. Для системы, состоящей из смеси идеальных газов

, Дж,

где . После преобразований с учетом, что , имеем:

Тогда А= - = - =0.

При отклонении от состояния равновесия dG>0 если d>0, то A<0 и если d<0 , то A>0.

Реакция слева направо может идти до тех пор, пока в системе присутствуют все реагенты, имеющиеся в левой части уравнения химической реакции, т.е.

. (17)

Фигурные скобки означают, что необходимо рассмотреть отношение (n для всех реагентов, участвующих в химической реакции, и выбрать наименьшее значение. Для рассматриваемой химической реакции моль. Для ХР, протекающей справа налево имеем:

(18)

Для рассматриваемой ХР моль.

Система уравнений химического равновесия и ее решение.

Система уравнений химического равновесия состоит в случае одной химической реакции из аппроксимации закона действующих масс в виде уравнения:

, (19)

и уравнения баланса энтальпии Н₃=Н₂ в виде:

. (20)

Эта система уравнений решается графоаналитическим способом.

В уравнении (20) -изобарный тепловой эффект химической реакции, определяемый по формуле:

. (21)

Задаваясь рядом значений температуры (например, Т=2000, 4000, 5000К), определяются значения величины пробега химической реакции по формуле (20) и строится график зависимости , которая при пересечении с прямой определяет максимальное значение температуры T_max..

---

Для определения коэффициентов аппроксимации а_-1 и а_ох , входящих в формулу (19), используется аппроксимация константы равновесия, выраженной через парциальные давления:

, (22)

которая зависит только от температуры и является линейной функцией от 1/Т. Коэффициенты а_-1 и а_о определяются из решения системы из двух уравнений (22)для двух значений температуры, например, 1000 и 3000К.

Натуральный логарифм константы К_р определяется по формуле

ln K_p= ln10, (23)

где lg K_p=-;

K-константа равновесия химической реакции распада i-го вещества на газообразные атомы; lg K_i определяется из справочной литературы для индивидуальных веществ, входящих в термодинамическую систему. Коэффициент аппроксимации а_ох определяется по формуле:

a, (24)

где - относительное давление в камере сгорания.

Задаваясь рядом значений пробега химической реакции  определяется значение функции f, входящей в формулу (19):

f=lnK_x(p,T)=_ilnx_i , (25)

,

f= . (26)

где K_x- константа равновесия, выраженная через молярные доли х_i, зависит от температуры и давления:

K_x(p,T)=K_p(T) , (27)

или lnK_x=lnK_p-.

Подставляя полученные значения функции f по (26) и коэффициентов а_-1 и а_ох по (22) и (24) в уравнение(19), определяется температура смеси газов для заданных значений пробега химической реакции и строится график зависимости T=T(). Пересечение этой зависимости с зависимостью =(T), полученной при решении уравнения (20), дает искомые равновесные значения  и Т₃, что является решением системы уравнений химического равновесия (19) и (20) в сечении 3-3 для случая протекания в камере сгорания ЖРД одной химической реакции.

Определяется погрешность определения пробега химической реакции

100%.

Определение состава реагентов в сечении 3-3 камеры сгорания ЖРД.

Состав смеси газов в состоянии равновесия при = определяется в следующем порядке:

, (28)

,

, ,

, , .

Определение параметров в сечении 3-3.

Для известного равновесного химического состава в сечении
3-3камеры сгорания (формулы (28)) и температуры Т_{3 равн}в состоянии равновесия системы при р₃=р₂ рассчитываются все параметры смеси газов в этом сечении по формулам (7)(16). Результаты расчетов термодинамических параметров в сечении 2-2 и 3-3 заносятся в сводную таблицу.

Все графы таблицы должны быть заполнены цифровыми значениями параметров. Буквенные обозначения даны в таблице для сведения о характере изменения параметров в изучаемых процессах.

Сводная таблица

результатов термодинамического расчета ракетного двигателя (образец)

Обозначение	Ед. измерен.	Сечение 2-2	Сечение 3-3	Сечение 4-4
Т	K	задано
р	Па	задано	р3=р2	задано
V	м3
n	моль	задано
n	
nг	
ncо		0
n		0
n	моль			n4=n3
				(xi)4=(xi)3
m	кг			(mi)4=(mi)3
m	
mг	
mcо		0
m		0
m	кг		m3=m2	m4=m3
iI=1				(i)4=(i)3
	кг/моль
	кг/м3
R	Дж/(кгК)
H	Дж		H3=H2
S	Дж/К			S4=S3
Cp	Дж/К
Cv	Дж/К
к	
a	м/с

---

Смотрите также файлы

• 12-13.doc

• appendix.doc

• 09.doc

• 14.doc

• 15.doc