Файл: Журнал практических работ по дисциплине Прикладная механика Вариант 17 студент гр. Ббпэ2131 Федотова А. О. Проверил к т. н., доцент Белобородова Т. Г. Стерлитамак 2023 практическая.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Институт химических технологий и инжиниринга федерального государственного бюджетного образовательного учреждения высшего образования
«Уфимский государственный нефтяной технический университет»
(ИХТИ ФГБОУ ВО в г. Стерлитамаке)
Кафедра «Оборудование нефтехимических заводов»
Журнал практических работ
по дисциплине: «Прикладная механика»
Вариант 17
Выполнила: студент гр. ББПЭ-21-31 Федотова А.О.
Проверил: к.т.н., доцент Белобородова Т.Г.
Стерлитамак 2023
ПРАКТИЧЕСКАЯ РАБОТА №1
Устройство и расчёт цилиндрических зубчатых передач
Задание: Рассчитать закрытую косозубую передачу одноступенчатого цилиндрического редуктора.
Исходные данные:
Р1=3,5 кВт
n1 = 750 об/мин
n2=375 об/мин
Т=104 ч
нереверсивный
постоянная
мощность на ведущем валу
частота вращения ведущей шестерни
частота вращения ведомого
зубчатого колеса
срок службы передачи
редуктор
нагрузка
Определяем передаточное число редуктора U по формуле:
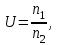(2.1)где n1 – частота вращения шестерни, об/мин;
n2 – частота вращения зубчатого колеса, об/мин.
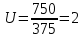
По ГОСТу 2185-66 округляем вычисленное значение до стандартного U=2 (с. 38).
Определяем угловые скорости вращения шестерни и зубчатого колеса ω, рад/с, по формуле:
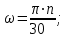
– шестерни:
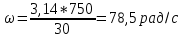
– зубчатого колеса:
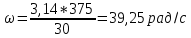
Определяем вращающий момент T1 Н∙м, на ведущем валу:
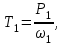(2.3)где P1 – мощность на ведущем валу, Вт:
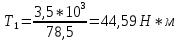
Определяем вращающий момент Т2, Н∙м, на ведомом валу:
T2=T1U; (2.4)
Т2 =44,59∙ 2 = 89,18 Н∙м.
Выбираем материал для изготовления шестерни и зубчатого колеса.
Исходя из условий работы редуктора, а также желаемых небольших габаритов, выбираем для изготовления шестерни и колеса сравнительно недорогую сталь 40Х с улучшением.
Для равномерного изнашивания зубьев и лучшей их прирабатываемости твёрдость шестерни НВ1 назначается больше твёрдости колеса HВ2.
Принимаем для колеса твердость на 30 единиц ниже, чем у шестерни: колесо – 245 НВ, шестерня – 285 НВ
Определяем допускаемые контактные напряжения [σ], МПа:
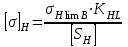, (2.5)где [SH] – коэффициент безопасности, [SH]=1,1÷1,2, таблица 2.2. (приложение 2, с. 38);
KHL – коэффициент долговечности KHL=1;
Н limB – предел контактной выносливости при базовом числе циклов, МПа (с. 39). Для колеса заготовка выбирается в пределах 90-120 мм диаметра, тогда НВ=245 (с. 38):
| σΗlimΒ =2·HB + 70; σΗlimΒ =2·245 + 70 = 560 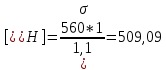МПа;  МПа. | (2.6) |
Определяем межосевое расстояние aW мм:
 | (2.7) |
где Ка – вспомогательный коэффициент для прямозубых Ka=43 (c. 39);
КHβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, КHβ=1
T2 – вращающий момент на ведомом валу редуктора
Т2=115,52 Нм;
Ψba – ширина зубчатого венца, Ψba = 0,4 (c. 40);
U – передаточное число редуктора, U=4.
 | |
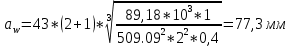Полученное значение межосевого расстояния аw округлить до ближайшего значения из ряда нормальных линейных размеров.
По ГОСТу 2185–66 принимаем значение межосевого расстояния аw=80 мм (таблица 2.8, c. 40).
Определяем модуль зацепления m, мм:
| m = (0,010,02)· 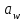 ;m = (0,010,02)·80 = 0,8 1,6 мм. | (2.8) |
Полученное значение модуля m выбрать из стандартного ряда модулей.
По ГОСТу 9563–60 принимаем значение модуля зацепления зубчатых колёс m=2 мм (таблица 2.9).
Примем предварительно угол наклона зубьев =100.
Определяем число зубьев шестерни Z1:
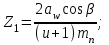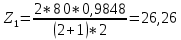  | (2.9) |
Полученное значение Ζ1 округлить до целого числа. Из условий уменьшения шума и отсутствия подрезания зубьев рекомендуется
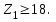
Принимаем Z1=26
Определяем число зубьев зубчатого колеса Z2:
| Z2=ZU; Z2=262=52. | (2.10) |
Принимаем значение Z2=52
Уточняем значение угла наклона зубьев:
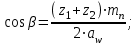(2.11)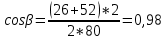
=
.
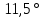
Определяем геометрические размеры передачи.
Определяем делительный диаметр шестерни d1, мм:
| d1=m·Z1/cos; d1 =2·26 / 0,98 = 53,06 мм. | (2.12) |
Определяем делительный диаметр колеса d2, мм:
| d2=m·Z2/cos; d2 =2·52 / 0,98 = 106,12мм. | (2.13) |
Определяем диаметры вершин зубьев шестерни da1, мм:
| da1=2·m + d1; da1 =2·2+53,06 = 57,06 мм. | (2.14) |
Определяем диаметры вершин зубьев колеса da2, мм:
| da2 = 2·m + d2; da2 =2·2 + 106,12 = 110,12 мм. | (2.15) |
Уточняем межосевое расстояние:
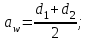(2.16)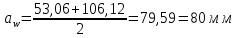
Определяем ширину колеса b2, мм:
| b2 = 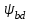 · aw , | (2.17) |
где
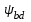– коэффициент ширины венца колеса 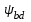=0,4 (таблица 2.7, c. 40):b2 =0,4·80 =32 мм.
Округляем ширину колеса и шестерни так, чтобы последняя цифра была бы «0» или «5».
Принимаем значение ширины колеса b2=35 мм.
Определяем ширину шестерни b1, мм:
| b1 =b2 +5; b1=35 + 5 = 40 мм. | (2.18) |
Определяем коэффициент ширины шестерни по диаметру
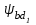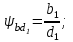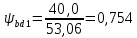:   | (2.19) |
Определяем окружную скорость колес V, м/с, и степень точности передачи:
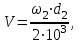 | (2.20) |
где d2 – делительный диаметр колеса;
ω2 – угловая скорость вращения колеса.
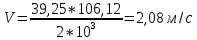
Для косозубых колес при V<4 м/с назначаем по ГОСТу 1643–81 9-ю степень точности (таблица 2.11).
Для проверки контактных напряжений определяем коэффициент нагрузки ΚΗ по формуле:
| ΚΗ=ΚΗβ·ΚΗα·ΚΗV, | (2.21) |
где ΚΗα – коэффициент, учитывающий распределение нагрузки
между зубьями. Принимаем ΚΗα=1;
ΚΗβ – коэффициент, учитывающий расположение зубчатых
колёс относительно опор, ΚΗβ=1 (c. 39);
ΚΗV – коэффициент динамической нагрузки, ΚΗV =1,01 (c. 41).
| ΚΗ =1·1·1,09=1,09. | |
Проверяем контактное напряжение σΗ, МПа:
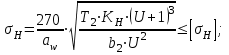 | (2.22) |
где аw – межосевое расстояние, мм;
b2 – ширина колеса, мм;
 | |
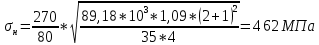Условие прочности по контактным напряжениям выполняется.
Допускаемая недогрузка передачи (σΗ<[σ]Η) не более 10% и перегрузка (σΗ<[σ]Η) до 5%.Где 462<509,09
Определяем силы, действующие в зацеплении.
Окружная сила Ft, Н:
Ft=2Т1 / d1, (2.23)
где Т1 – крутящий момент на шестерне, Нмм;
d1 – делительный диаметр шестерни, мм;
Ft=244.59103 / 53,06=1681 Н.
Определяем радиальную силу Fr, H:
| Fr=Ft·tg/cos, | (2.24) |
где α – угол зацепления, принятый по ГOCTy 13755–81;
α =20º;
Fr =1681·tg20º / 0,98 = 624 H.
Определяем осевую силу Fa, Н:
Fa