Файл: Тригонометрия.docx

Частное профессиональное образовательное учреждение

«Башкирский экономико-юридический колледж (БЭК)»
Реферат

на тему: «Тригонометрия»

Принял:

Исламов Ф. Ф.

Выполнила:

студентка 1 курса

Николаева Ю. Ф.


Нефтекамск

2023
Содержание

Введение……………………………………………………………...3

§1. Тригонометрические функции в действительной области

1. 
   История тригонометрии……………………………..……...4
   
2. 
   Определение тригонометрических функций……………...7
   
3. 
   Область определения и множество значений……………..9
   
4. 
   Четность, нечетность, периодичность………………........10
   
5. 
   Производные..…………………………………………..….11
   
6. 
   Графики тригонометрических функций. ……………......13
   
7. 
   Разложение в ряд………………………………………......16
   
8. 
   Формулы тригонометрии………………………………….17
   

§2. Тригонометрические функции в школьном курсе

2.1. Программа изучения тригонометрических функций…....20

2. 
   Анализ учебников………………………………………….22
   
3. 
   Дидактические материалы………………………………...28
   

Заключение…………………………………………………………33

Список использованной литературы……………………………..34



Введение

Тригонометрия - раздел математики, в котором изучаются тригонометрические функции. Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела.

В основном тригонометрические функции изучаются в курсе алгебры и начал анализа общеобразовательной школы. Существует несколько различных подходов к изучению данной темы в школьном курсе, и учитель, особенно начинающий, легко может запутаться в том, какой подход является наиболее подходящим. А ведь тригонометрические функции представляют собой наиболее удобное и наглядное средство для изучения всех свойств функций, а в особенности такого свойства многих природных процессов как периодичность. Поэтому их изучению следует уделить пристальное внимание. Все выше сказанное и обуславливает актуальность выбора темы для данной курсовой работы.

---

Целью курсовой работы является обобщение и систематизация свойств тригонометрических функций в школе и вузе.

Задачи:

1. 
   Собрать и систематизировать теоретический материал по тригонометрическим функциям в вузе (в действительной области);
   
2. 
   Ознакомиться с введением тригонометрических функций в общеобразовательной школе (базовый уровень);
   
3. 
   Рассмотреть задачи по теме в общеобразовательной школе (базовый уровень);
   

§1. Тригонометрические функции в действительной области

1. 
   История тригонометрии
   

Тригонометрия — греческое слово и буквально означает измерение треугольников (Триггунон — треугольник и измерение Метрю).

В этом случае под измерением треугольников следует понимать треугольное решение, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, но также и задачи планаметрии, стереометрии, астрономии и другие даны задачам решения треугольников.

Появление тригонометрии связано с астрономией и строительством.

Хотя название науки появилось сравнительно недавно, многие понятия и факты, связанные с тригонометрией, были известны уже две тысячи лет назад.

Решения для треугольников, основанные на зависимостях между сторонами и углами треугольника, были впервые найдены древнегреческими астрономами Гиппархом (II в. до н.э.) и Клавдием Птолемеем (II в. н.э.). Позже отношения между сторонами треугольника и его углами стали называться тригонометрическими функциями.

Значительный вклад в развитие тригонометрии внесли арабские ученые ал-Батани (850-929 гг.) и абу-л-Вафа Мухаммад бин Мухаммад (940-998 гг.), создавшие таблицы с синусоидальными кривыми и касательными после 10′ с точностью до 1/604 гг. Индийский ученый Бхаскара (род. 1114 г., год смерти неизвестен) и азербайджанский астроном и математик Насираддин Туси Мухаммад (1201-1274 гг.) уже знали теорему синуса. Кроме того, Насираддин Туси представил плоскую и сферическую тригонометрию как отдельную дисциплину в своем труде «Трактат о полном квадричастии».

В долгой истории существует понятие синуса. Фактически, различные соотношения сечений треугольника и круга (а по существу, и тригонометрические функции) встречаются уже в III в. до н.э. в трудах великих математиков Древней Греции — Евклида, Архимеда, Аполлонии Пергусской. В римский период эти отношения систематически изучались Менелаем (I в. н.э.), хотя конкретное название им не давалось. Современный синус a, например, изучался как полуаккорд, на котором центральный угол лежит в размере a, или как двухдуговой аккорд.

---

Уже в IV-V веке в астрономических трудах великого индийского ученого Ариабхаты, чье имя было дано первому индийскому спутнику Земли, существовал особый термин. Он назвал отрезок АМ (рис. 1) аргаджива (арга — половина, джива — луковая струна, которая напоминает аккорд). Позже появилось более короткое имя Джива. Арабские математики в IX в. заменили это слово на арабское слово jib (выпуклость). В переводе арабских математических текстов в этом столетии он был заменен на латинский синус (синус — кривизна, изгиб).

Слово «косинус» намного моложе. Косинус — это аббревиатура латинского термина для полного синуса. «лишний синус» (или иначе «лишняя дуга»).

Касательные появились в связи с решением задачи определения длины тени. Тангент (как и кокангент) был введен в X. столетие арабский математик Абу-л-Вафа, который создал первые таблицы для нахождения тангенса и кокангента. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенты были заново открыты только в XIV веке немецким математиком и астрономом Реджимонтаном (1467 г.). Он доказал теорему о тангенте. Regimontan также сделал подробные тригонометрические таблицы, благодаря его работам плоские и сферические тригонометрии стали отдельной дисциплиной в Европе.

Название «касательные», происходящее от латинского tangens (to touch), появилось в 1583 году, тангенс переводится как «касание» (линия касания — касательная к одному кругу).

Дальнейшее развитие тригонометрии состоялось в трудах выдающегося астронома Николая Коперника (1473-1543) — создателя мировой гелиоцентрической системы Тихо Браге (1546-1601) и Иоганна Кеплера (1571-1630), а также в трудах математика Франсуа Виета (1540-1603), который полностью решил задачу определения всех элементов плоского или сферического треугольника на три даты.

Долгое время тригонометрия была чисто геометрической. Факты, которые мы сейчас формулируем в виде тригонометрических функций, были сформулированы и доказаны с помощью геометрических концепций и высказываний. Так было уже в средние века, хотя иногда использовались аналитические методы, особенно после появления логарифмов. Пожалуй, наибольший стимул для развития тригонометрии возник в связи с решением астрономических задач, представлявших большой практический интерес (например, для решения задач определения положения корабля, прогнозирования отключения электроэнергии и т.д.). Астрономов интересовали отношения между сторонами и углами сферических треугольников. И надо сказать, что математики древнего мира успешно справились с поставленными задачами.

---

С XVII века тригонометрические функции стали использоваться для решения уравнений, задач механики, оптики, электротехники, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, изучения переменного тока и др. Поэтому тригонометрические функции были всесторонне и глубоко исследованы и приобрели значение для всей математики.

Аналитическая теория тригонометрических функций была разработана в основном Леонардом Эйлером (1707-1783), выдающимся математиком XVIII века, членом Санкт-Петербургской Академии наук. Большое научное наследие Эйлера включает в себя блестящие результаты, связанные с математическим анализом, геометрией, теорией чисел, механикой и другими математическими приложениями. Именно Эйлер первым ввел известные определения тригонометрических функций, начал рассматривать функции любого угла, и получил формулы редукции. По словам Эйлера, тригонометрия получила форму расчета: различные факты стали доказываться формальным применением формул тригонометрии, доказательства стали намного компактнее.

Таким образом, тригонометрия, зародившаяся как наука о разрешении треугольников, со временем переросла в науку о тригонометрических функциях.

Позже часть тригонометрии, изучающую свойства тригонометрических функций и связь между ними, стала называться гониометрией (в переводе — наука об измерении угла, с греческого gwnia — угол, metrew — мера). В последнее время термин «гониометрия» практически не используется.

2. 
   Определение тригонометрических функций
   

Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.

К тригонометрическим функциям относятся следующие 4 функции: синус, косинус, тангенс, котангенс. Для каждой из указанных функций существует 

---

обратная тригонометрическая функция: арксинус, арккосинус, арктангенс, арккотангенс.

Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r = 1. На окружности обозначена точка M (x, y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.



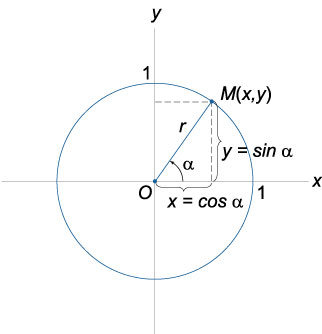
Синусом угла α называется отношение ординаты y точки M (x, y) к радиусу r: sin α = y/r. Поскольку r = 1, то синус равен ординате точки M (x ,y).

Косинусом угла α называется отношение абсциссы x точки M (x,y) к радиусу r: cos α = x/r = x.

Тангенсом угла α называется отношение ординаты y точки 

M (x, y) к ee абсциссе x: tg α = y/x, x ≠ 0.

Котангенсом угла α называется отношение абсциссы x точки 

M (x, y) к ее ординате y: ctg α = x/y, y ≠ 0. 

В единичном круге проекции x, y точки M (x, y) и радиус r образуют прямоугольный треугольник, в котором x, y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:

Синусом угла α называется отношение противолежащего катета к гипотенузе. 

Косинусом угла α называется отношение прилежащего катета к гипотенузе. 

Тангенсом угла α называется отношение противолежащего катета к прилежащему. 

Котангенсом угла α называется отношение прилежащего катета к противолежащему. 

3. 
   . Область определения и множество значений тригонометрических функций
   

Каждому действительному числу x соответствует единственная точка единичной окружности, получаемая поворотом точки (1;0) на угол x радиан. Для этого угла определены sin x и cos x. Тем самым каждому действительному числу x поставлены в соответствие числа sin x и cos x, т.е. на множестве R всех действительных чисел определены функции y = sin x и y = cos x. Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.

Чтобы найти множество значений функции y = sin x, нужно выяснить, какие значения может принимать y при различных значениях x, т.е. установить, для каких значений y есть такие значения x, при которых sin x = y. Известно, что уравнение sin x = a имеет корни, если |a| ≤ 1, и не имеет корней, если |a|> 1. Следовательно, множеством значений функции y = sin x является отрезок -1 ≤ y ≤ 1. Аналогично множеством значений функции y = cos x также является отрезок -1 ≤ y ≤ 1.

---