Файл: Тригонометрия.docx

Формулы приведения

2. 
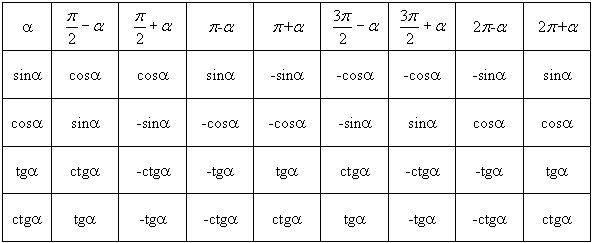
   Тригонометрические функции в школьном курсе
   
   1. 
      Программа изучения тригонометрических функций в общеобразовательной школе
      

Основными целями изучения тригонометрических функций числового аргумента являются:

1. Ознакомление учащихся с новым видом трансцендентных функций;

2. Развитие навыков вычислительной практики (работа с трансцендентными функциями зачастую требует громоздких вычислений);

3. Наглядная иллюстрация всех основных свойств функций (в особенности периодичности);

4. Установление межпредметных связей с практикой (изучение колебаний маятника, электрического тока, волновой теории света невозможны без знаний о тригонометрических функциях).

В изучении тригонометрических функций можно выделить следующие этапы:

1. Первое знакомство с тригонометрическими функциями углового аргумента в геометрии. Значение аргумента рассматривается в промежутке (0^о;90^о). На этом этапе учащиеся узнают, что sin, сos, tg и ctg угла зависят от его градусной меры, знакомятся с табличными значениями, основным тригонометрическим тождеством и некоторыми формулами приведения.

2. Обобщение понятий синуса, косинуса, тангенса и котангенса для углов (0^о;180^о). На этом этапе рассматривается взаимосвязь тригонометрических функций и координат точки на плоскости, доказываются теоремы синусов и косинусов, рассматривается вопрос решения треугольников с помощью тригонометрических соотношений.

3. Введение понятий тригонометрических функций числового аргумента.

4. Систематизация и расширение знаний о тригонометрических функциях числа, рассмотрение графиков функций, проведение исследования, в том числе и с помощью производной.

---

Существует несколько способов определения тригонометрических функций. Их можно подразделить на две группы: аналитические и геометрические. К аналитическим способам относят определение функции у = sin х как решения дифференциального уравнения f ^''(х)=-c*f(х) или как сумму степенного ряда sin х = х – х³ /3!+ х⁵ /5!

К геометрическим способам относят определение тригонометрических функций на основе проекций и координат радиус-вектора, определение через соотношения сторон прямоугольного треугольника и определения с помощью числовой окружности. В школьном курсе предпочтение отдается геометрическим способам в силу их простоты и наглядности.

Изучение тригонометрических функций в школьном курсе имеет некоторые особенности. Во-первых, до изучения тригонометрических функций, рассматривались функции вида у=f(x), где х и у – некоторые действительные числа, здесь же - углу ставится в соответствие число, что является несколько непривычным для учащихся. Кроме того, раньше все функции задавались формулами, в которых явным образом был указан порядок действий над значениями аргумента для получения значений функции. Теперь же учащиеся сталкиваются с функциями, заданными таблично. 

Изучая тригонометрические функции, учащиеся лучше начинают разбираться в сущности самого понятия функции. Они начинают осознавать, что функцией может быть зависимость между любыми множествами объектов, даже если они имеют различную природу.

2. 
   Анализ учебников по алгебре и начала анализа по теме «Тригонометрические функции»
   

Общеобразовательная школа. Мордкович А. Г «Алгебра и начала анализа. 10-11 кл.»

Отдельно изучается тема “Тригонометрические функции” – 23 часа. На изучение темы “Тригонометрические уравнения” отводится 10 часов и 16 часов – на тему “Преобразование тригонометрических выражений”. Будем рассматривать методические особенности учебника в контексте этих двух последних тем, т.к. обучение решению тригонометрических уравнений имеет место и в теме “преобразования тригонометрических выражений”.

---

Тема “Тригонометрические уравнения”. Первые представления о решении простейших тригонометрических уравнений. Арккосинус и решение уравнения cos x = a. Арксинус и решение уравнения sin x = a. Арктангенс и решение уравнения tgx = a, арккотангенс и решение уравнения ctgx = a. Тригонометрические уравнения (два основных метода решения тригонометрических уравнений: разложение на множители и введение новой переменной, решение однородных уравнений).

Тема “Преобразование тригонометрических выражений”. Синус и косинус суммы аргументов. Синус и косинус разности аргументов. Тангенс суммы и разности аргументов. Формулы двойного аргумента. Формулы понижения степени. Преобразование сумм тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в сумму. Преобразование выражения вида A sin x + B cos x  к виду C sin(x + t) .

При изучении темы “Тригонометрические уравнения” автор учебника дает возможность школьнику прочувствовать специфику тригонометрических уравнений. Перечень основных уравнений здесь составляют уравнения простейшие, уравнения, при решении которых применяется метод введения новой переменной: однородные уравнения и уравнения, сводящиеся к квадратным с помощью основного тригонометрического тождества. Также перед тем, как выводить формулы для решения простейших тригонометрических уравнений, автор напоминает учащимся, что они уже знают, как решать уравнения с помощью числовой окружности, и только после этого вводит их в проблемную ситуацию, связанную с решением уравнений типа   .

Только после того, как ввел учащихся в проблемную ситуацию, он вводит новые для них понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Тем самым, при такой схеме изложения выделяются два обстоятельства.

1. 
   При такой схеме изложения реализуется метод проблемного изложения материала. Учащийся попадает в нештатную ситуацию, для описания которой недостаточно тех средств, которые имеются в его математическом языке. Становится очевидна необходимость введения нового термина, нового понятия, новой математической модели и нового обозначения.
   
2. 
   При изложении материала не употребляется термин “обратные тригонометрические функции”. Тем самым реализуется принцип доступности изложения учебного материала.
   

---

Отличительной особенностью этого учебника является то, что для решения простейших тригонометрических уравнений (как и для решения однородных уравнений) в учебнике фактически используется алгоритм:

1. 
   Составить общую формулу;
   
2. 
   Вычислить значение арксинуса (арккосинуса и т.д.);
   
3. 
   Подставить найденное значение в общую формулу.
   

При изучении темы “тригонометрические уравнения” рассматриваются также примеры на отбор корней в тригонометрических уравнениях, причем, весь этот материал изучается до введения преобразований тригонометрических выражений.

После темы “Тригонометрические уравнения” изучается тема “Преобразования тригонометрических выражений”, где приводятся уже специальные методы решения тригонометрических уравнений.

Главное отличие учебника А.Г. Мордковича от остальных рассмотренных здесь учебников, как было уже сказано выше, состоит в новой схеме изложения материала: “функция – уравнения – преобразования”. Данная схема построения материала позволяет в соответствии с уровнем развития учащихся, не перегружая его память большим количеством формул, научить ученика решать тригонометрические уравнения, причем, делать это вполне осознанно, т.е. с пониманием всей сути того, что он делает.

Базовый уровень. Колмогоров А. Н. “Алгебра и начала анализа. 10–11 кл.”

На изложение темы “Тригонометрические уравнения” здесь отводится 14 часов. Рассмотрим содержание материала: арксинус, арккосинус и арктангенс числа. Простейшие тригонометрические уравнения. Решение тригонометрических уравнений, систем уравнений.

Основная цель – сформировать у учащихся умение решать простейшие тригонометрические уравнения и ознакомить с основными приемами решения тригонометрических уравнений.

Введению понятий арксинуса, арккосинуса и арктангенса предшествует рассмотрение теоремы о корне. Основное внимание здесь нужно уделить разъяснению смысла указанных выше понятий, а также формированию умения находить табличные значения, что необходимо для безошибочного решения тригонометрических уравнений.

Вывод формул корней простейших тригонометрических уравнений основывается на изученных свойствах соответствующих функций.

Материал, представленный в учебнике, соответствует обязательному минимуму обучения, однако для учащихся 10 класса материал, представленный в учебнике,

---

является достаточно трудным для понимания, т.к. здесь мы имеем чересчур сжатое изложение.

В данном учебнике мы сталкиваемся с достаточно известной схемой изложения материала по тригонометрии – сначала в головы учеников пытаются “вбить” все известные формулы курса тригонометрии, а потом научить решать тригонометрические уравнения. В результате мы получаем достаточно банальную ситуацию: тригонометрические уравнения и преобразования тригонометрических выражений так и остаются в голове учащихся на разных берегах реки. Получается, что, пользуясь схемой изложения материала, предложенной в данном учебнике, мы изучаем с учащимися формулы ради формул. Мы получаем обучение без развития. Для ученика 10 класса так и остаются невыясненными следующие факты:

1. 
   Что же все-таки это такое – арксинус, арккосинус и арктангенс числа?
   
2. 
   Почему раньше при решении уравнения мы получали конечное число корней, а теперь – бесконечное?
   
3. 
   Откуда в записи корней тригонометрического уравнения появился “хвост” πn или 2πn. Распространенная ошибка учащихся при записи корней уравнения sin x = a – ошибка следующего вида: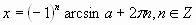  , что вполне очевидно, ведь y = sin x – функция периодическая и период этой функции равен 2πn.
   
4. 
   Что такое (-1)ⁿ  в записи корней уравнения  sin x = a и почему его нет при записи корней уравнения cosx = a , а вместо этой “страшной” конструкции при решении уравнения cos x = a  получаем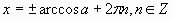 . Здесь, кстати, мы сталкиваемся с ошибкой такого рода: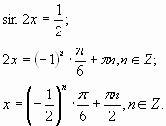
   
5. 
   Наконец, возникают ситуации, когда при решении тригонометрического уравнения нам необходимо осуществить отбор корней, а вот эти ситуации не рассматриваются в предложенном учебнике.
   

Базовый уровень. Алимов А. Ш. “Алгебра и начала анализа 10–11 кл.”

На изучение темы отводится 18 часов. Уравнение cos x = a, sin x = a. Уравнение tgx = a. Решение тригонометрических уравнений. Примеры решения простейших тригонометрических неравенств.

---