Добавлен: 10.11.2023
Просмотров: 264
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Основная цель – сформировать умение решать простейшие тригонометрические уравнения, познакомить учащихся с некоторыми приемами решения тригонометрических уравнений.
Изучение темы начинается с рассмотрения конкретных простейших уравнений, решение которых иллюстрируется на единичной окружности, что хорошо подготовлено материалом главы “Тригонометрические формулы”.
Понятия арксинуса, арккосинуса, арктангенса вводятся до знакомства с обратными тригонометрическими функциями (тригонометрические функции изучаются в 11 классе) и иллюстрируются также на единичной окружности. В дальнейшем не следует уделять много внимания упражнениям на нахождение значений и использование свойств арксинуса, арккосинуса, арктангенса: все это будет закрепляться в ходе решения уравнений. При решении уравнений полезно иллюстрировать нахождение корней на единичной окружности: это позволит осознанно применять формулы корней.
Решение более сложных тригонометрических уравнений рассматривается на примерах уравнений, сводящихся к квадратным, уравнений вида a sin x + b cos x = c, уравнений, решаемых разложением левой части на множители.
Материал в учебнике соответствует обязательному минимуму обучения, весьма доступен для учащихся 10 класса. Можно даже заметить, что авторы при решении уравнений предлагают иллюстрировать нахождение корней на единичной окружности, в дальнейшем это позволит избежать вопросов о количестве корней тригонометрического уравнения и частично ликвидирует трудность в восприятии учащимися таких элементов, как (-1)n arcsin a + ... и + arccos a + ... . Однако у ученика 10 класса так и остаются невыясненными вопросы, связанные с понятием арксинуса, арккосинуса и арктангенса, с появлением периода в записи ответа к тригонометрическому уравнению, с появлением множителя (-1)nи, наконец, проблема отбора корней так и остается открытой.
В учебнике решенным является вопрос учеников о количестве корней тригонометрического уравнения, но при изложении материала по тригонометрии мы снова сталкиваемся с известной схемой изложения материала “функция – преобразования – уравнения”. Т.е. снова формулы выведены на первое место, а простейшим уравнениям внимания уделено недостаточно.
-
Дидактические материалы
Самостоятельная работа
Вариант 1
1). Вычислить значение sin α , если cos α =
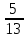 и
и 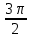 < α < 2π
< α < 2π2). Вычислить значение tg α и ctg α, используя данные задания 1.
3). Упростить выражение: cos4 α + sin2 α × cos2 α .
Вариант 2
1). Вычислить значение cos α , если sin α = 0,8 и
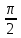 < α < π
< α < π2). Вычислить значение tg α и ctg α, используя данные задания 1)
3). Упростить выражение: cos2 α × tg2 α + cos2 α
Вариант 3
1). Вычислить значение tg α, если ctg α = -3 и 270° < α < 360°
2). Вычислить значение sin α и cos α, используя данные задания 1.
3). Упростить выражение:
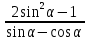
Вариант 4
1). Вычислить значение ctg α, если tg α = -2,4 и
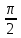 < α < π
< α < π2). Вычислить значение sin α и cos α, используя данные задания 1.
3). Упростить выражение:
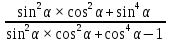
Вариант 5
1). Вычислить значение sin α , если cos α = 0,8 и 0° < α < 90°
2). Вычислить значение tg α и ctg α, используя данные задания 1.
3). Упростить выражение:
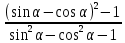
Практическое задание №1
Тема: Преобразование графиков тригонометрических функций.
Цель: закрепить методику построения графиков тригонометрических функции, правила преобразования графиков.
| Вариант №1 | Вариант №2 |
| 1. Постройте график функции 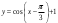 ; ;2. Укажите промежутки возрастания и убывания функции; 3. Определите нули функции. | 1. Постройте график функции 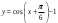 ; ;2. Укажите промежутки возрастания и убывания функции; 3. Определите нули функции. |
| Вариант №3 | Вариант №4 |
| 1. Постройте график функции 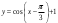 ; ;2. Укажите промежутки возрастания и убывания функции; 3. Определите нули функции. | 1. Постройте график функции 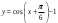 ; ;2. Укажите промежутки возрастания и убывания функции; 3. Определите нули функции. |
Практическое задание №2
Тема: Исследование тригонометрических функций и построение их графиков
Цель: Изучение свойств тригонометрических функций. Отработать методику построения тригонометрических функций.
| Вариант №1 | Вариант №2 |
| 1. Постройте график функции. По графику найдите: 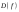 ; ; 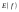 ; участки возрастания и убывания функции; наибольшее и наименьшее значение. ; участки возрастания и убывания функции; наибольшее и наименьшее значение. | |
| 1) 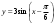 2) 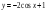 | 1)  2) 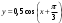 |
| 2. Известно, что 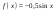 . Найдите . Найдите 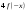 . . | 2. Известно, что 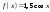 . Найдите . Найдите 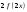 . . |
| 3. Известно, что 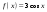 . Найдите . Найдите 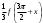 . . | 3. Известно, что 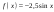 . Найдите . Найдите 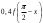 . . |
| 4. Решите графически уравнение | |
| 1) 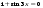 ; ;2) 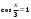 | 1) 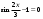 ; ;2) 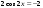 |
Практические задание №3
Тема: Преобразование тригонометрических выражений
Цель: Научить применять основные тригонометрические формулы при преобразовании тригонометрических выражений.
| Вариант №1 | ||||
| Упростить выражения | ||||
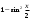 | 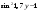 | 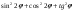 | ||
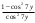 | 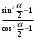 | 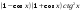 | ||
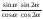 | 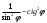 | 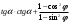 | ||
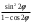 | 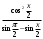 | 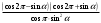 | ||
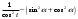 | 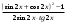 | |||
| Вариант №2 | ||||
| Упростить выражения | ||||
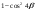 | 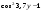 | 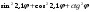 | ||
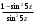 | 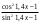 | 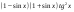 | ||
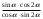 | 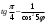 | 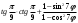 | ||
Упражнения
1. Написать уравнение касательной к синусоиде у = sin x в точке с абсциссой:
а) х = 0; б) х = π/2; в) х = 3/2 π; г) х = π/4; д) х = π.
2. Написать уравнение касательной к косинусоиде у = cos x в точке а абсциссой:
а) х = 0; б) х = π/2; в) х = 3/2 π; г) х = π/4; д) х = π.
3. Найти производные следующих функций:
у = 3 sin х + 2 cos х. у = sin х • cos х.
у = 4 sin х — 5 cos х. у = х2 sin х.
у = — sin х + 7 cos х. у = х2 cos х.
у = — 6 sin х — 9 cos х. у = cos2 x/2 .
у = sin2 х. у = (5х + sin х) (х2 — cos х).
у = cos2 х. у = (1 — 2 sin х) (1 — 3 cos х).
Самостоятельная работа
Упростите:
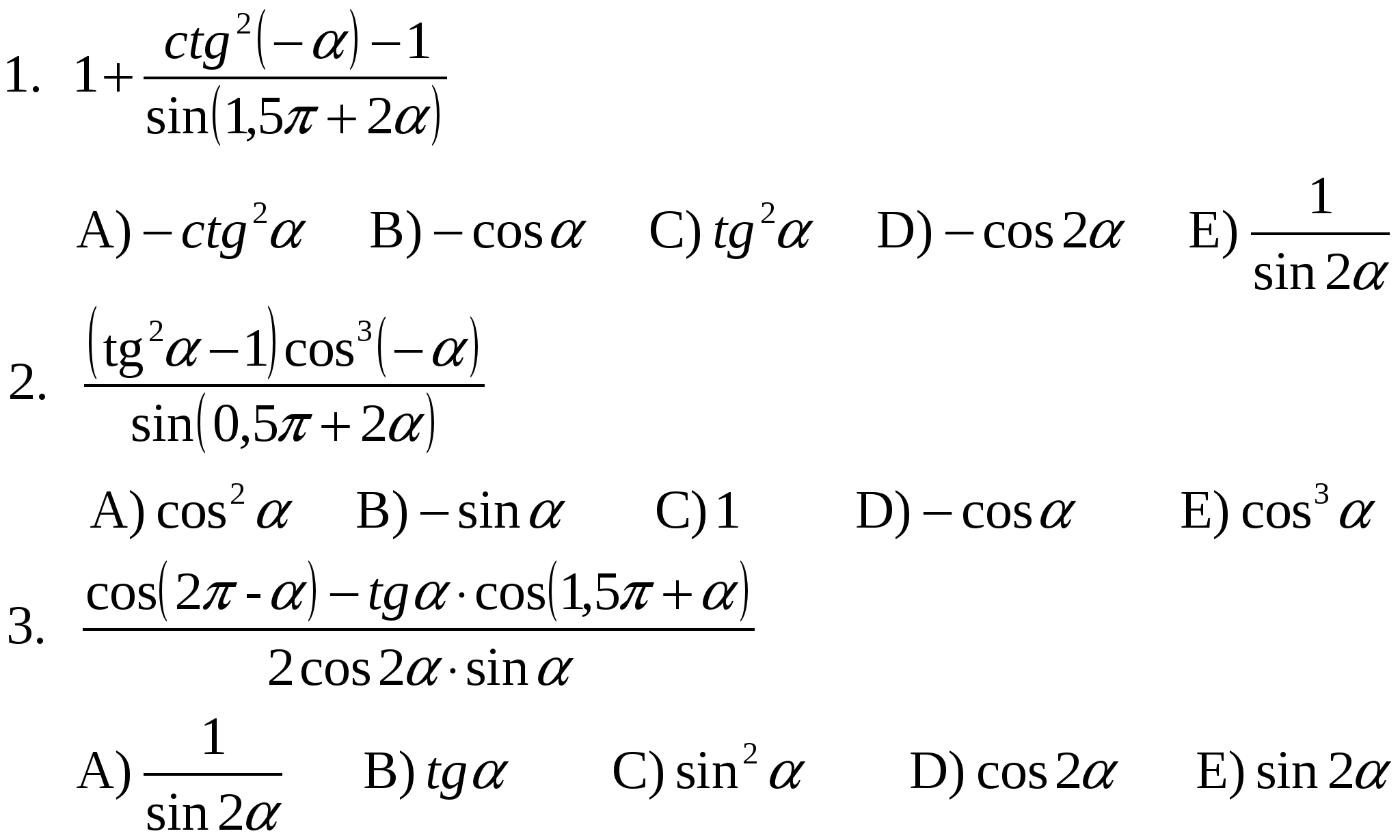

Заключение
В связи с многочисленными приложениями тригонометрических функций изучение этой темы в школе и в вузе имеет важное теоретическое и практическое значение. В работе рассмотрены свойства функций в действительной области в вузе. Представлен теоретический, практический материал изучения темы в школе и задачи ЕГЭ.
Курсовая работа будет полезна учащимся, учителям и студентам вузов.
Список использованной литературы
-
Алгебра и начала математического анализа: учеб. для 10-11 кл. общеобразовательных учреждений / А. Н. Колмогоров [и др.]; под ред. А.Н. Колмогорова. – 16-е изд. – М.: Просвещение, 2007. – 320 с. -
Алгебра и начала математического анализа. 10-11 классы. Задачник для учащихся общеобразовательных учреждений (базовый уровень) / Под ред. А. Г. Мордковича. – 9-е изд., перераб. – М.: Мнемозина, 2008. – 239 с. -
Алгебра и начала анализа: 9-11-е выпускные классы: учебное пособие школьникам, абитуриентам, учителям / под ред. Е. В. Якушева. – М.: АСТ-пресс школа, 2002. - 415 с. -
Алгебра и начала анализа. Учебник для 10-11 классов / А.Ш. Алимов [и др.]; под ред. А. Ш. Алимова. - 15-е изд. - М.: Просвещение, 2007. – 384 с. -
Башмаков, М. И. Алгебра и начала анализа. Учебник для 10-11 кл. сред. шк. / М. И. Башмаков. – М.: Дрофа, 2005. – 352 с. -
Вавилов, В. В. Задачи по математике / В. В. Вавилов, И. И. Мельников, С. Н. Олехник. - М.: Наука, 2007. – 328 с. -
Галицкий, М. Л. Углубленное изучение алгебры и начала математического анализа. 10-11 класс. Методические рекомендации / М. Л. Галицкий, С. И. Шварцбурд, М. М. Мошкович. – 3-е изд. дораб. – М.: Просвещение, 2015. – 160 с. -
Дудницын, Ю. П. Контрольные работы по алгебре и началам анализа: 10 класс: материалы для уровневого обучения: к учебнику под ред. А.Н. Колмогорова «Алгебра и начала анализа. 10-11 классы» / Ю.П. Дудницын, В.Л. Кронгауз – М.: Издательство «Экзамен», 2007. – 63 с. -
Звавич, Л. И. Алгебра и начала анализа, 8-11 кл. Пособие для школ и классов с углубленным изучением математики / Л. И. Звавич, Л. Я. Шляпочник, М В. Чинкина. - М.: Дрофа, 2002. - 352 с. -
Зив, Б. Г. Дидактические материалы по алгебре для 10-11 классов / Б. Г. Зив, В. А. Гольдич. – СПб.: Петроглив 2013. – 216 с. -
Ивлев, Б. И. Дидактические материалы по алгебре и началам анализа для 11 класса / Б. М. Ивлев, С. М. Саакян, С. И. Шварцбурд. – М.: Просвещение, 2007. – 176 с. -
Карп, А. П. сборник задач по алгебре и началам анализа, 10-11 классы / А. П. Карп. - М.: Просвещение, 1995. – 176 с. -
Лысенко, Ф. Ф. Математика. Подготовка к ЕГЭ-2013: учебно-методическое пособие / Ф. Ф. Лысенко, С. Ю. Кулабухова. – Ростов-на-Дону: Легион, 2012. – 416 с. -
Мордкович, А. Г. Алгебра и начала анализа. 10-11 класс / А. Г. Мордкович. - 2-е изд. – М.: Мнемозина, 2001. – 335 с. -
Никольский, С. М. Алгебра и начала математического анализа. 11 класс / С. М. Никольский. - 8-е изд. – М.: Просвещение, 2009. – 464 с. -
Потапов, М. К. Математика. Готовимся к экзамену / М. К. Потапов, С. Н. Олехник, Ю. В. Нестеренко. - М.: Русское слово, 2001. – 352 с. -
Ященко, И. В. Математика: 30 типовых вариантов экзаменационных работ для подготовки к ЕГЭ / И. В. Ященко, И. Р. Высоцкий, А. С. Трепалин. - Москва: АСТ: Астрель, 2014. – 1