Файл: Тригонометрия.docx

Функция y = tg x определяется формулой y = tg x = sin x/cos x. Эта функция определена при тех значениях x, для которых cos x ≠ 0. Известно, что cos x = 0 при x = π/2 + πn, n Є Z. Следовательно, областью определения функции y = tg x является множество чисел x ≠ π/2 + πn, n Є Z. Так как уравнение tg x = a имеет корни при любом действительном значении a, то множеством значений функции y = tg x является множество R всех действительных чисел.


1.4. Четность, нечетность, периодичность тригонометрических функций

Известно, что для любого значения x верны равенства sin (-x) = -sin x, cos (-x) = cos x. Следовательно, y = sin x — нечетная функция, а y = cos x — чётная функция. Так как для любого значения x из области определения функции y = tg x верно равенство tg (-x) = -tg x, то y = tg x — нечетная функция.

Известно, что для любого значения x верны равенства sin (x + 2π) = sin x, cos (x + 2π) = cos x. Из этих равенств следует, что значения синуса и косинуса периодически повторяются при изменении аргумента на 2π. Такие функции называются периодическими с периодом 2π.

Число 2π является наименьшим положительным периодом функции y = cos x, также и для функции y = sin x. π - наименьший положительный период функции tg x.

1.5. Производные тригонометрических функций

Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.

По определению производной для функции синуса имеем  .

Воспользуемся формулой разности синусов:

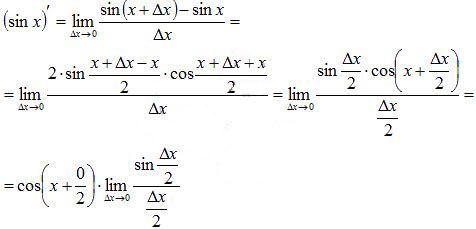
Осталось обратиться к первому замечательному пределу:


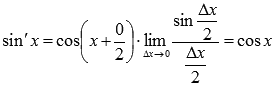
Таким образом, производная функции sin x есть cos x.

Абсолютно аналогично доказывается формула производной косинуса.



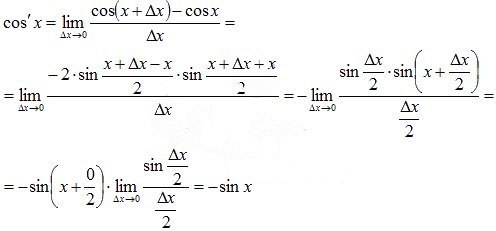
Следовательно, производная функции cos x есть –sin x.

Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования (

---

производная дроби).



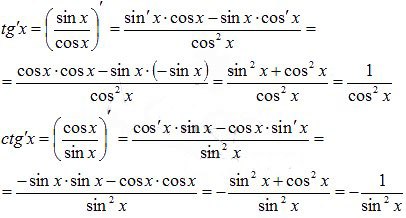
1.6. Графики тригонометрических функций

Функция y=sin x.



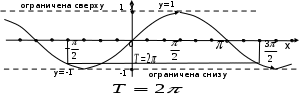
Синусом  аргумента х (sin(x)) называется ордината точки пересечения окружности единичного радиуса с центром в начале координат и луча, выходящего из начала координат и составляющего с осью ОХ угол х. Областью определения функции sin(x) является вся числовая прямая – промежуток (-∞;+∞).

Область значений лежит в промежутке [-1;1].
Функция sin(x)  периодична, период Т = 2П. Функция sin(x)  является нечетной, так как sin(-x)=-sin(x). График функции sin(x) называют синусоидой.  Синусоида пересекает ось ОХ в точках (kП;0). Синусоида имеет экстремумы-максимумы в точках   и экстремумы-минимумы в точках  .
Функция y=cos x.



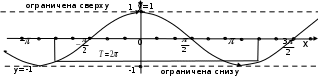
Косинусом  аргумента х (cos(x)) называется абсцисса точки пересечения окружности единичного радиуса с центром в начале координат и луча, выходящего из начала координат и составляющего с осью ОХ угол х. Областью определения функции cos(x) является  вся числовая прямая - промежуток (-∞;+∞).

Область значений лежит в промежутке [-1;1]. Функция cos(x) периодична, период Т = 2П. Функция cos(x) является четной, так как cos(-x)=cos(x). График функции cos(x), называют косинусоидой. 
Косинусоида пересекает ось ОХ в точках  . 
Синусоида имеет экстремумы-максимумы в точках (2Пk;1) и экстремумы-минимумы в точках (П+2Пk;-1)
Функция y=tg x.

---

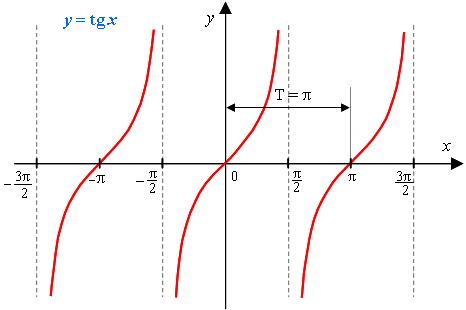
Тангенсом называется соотношение  . Областью определения функции tg(x) является вся числовая прямая , кроме точек   - в этих точках функция не определена, так как, по определению  , а в точках  . А на ноль делить нельзя. Область значений лежит в промежутке (-∞;+∞). Функция tg(x) периодична, период Т = П. Прямые    являются асимптотами. На каждом из промежутков     функция возрастает. График функции tg(x), называют тангенсоидой.  Тангенсоида пересекает ось ОХ в точках  , 
Функция y=ctg x.



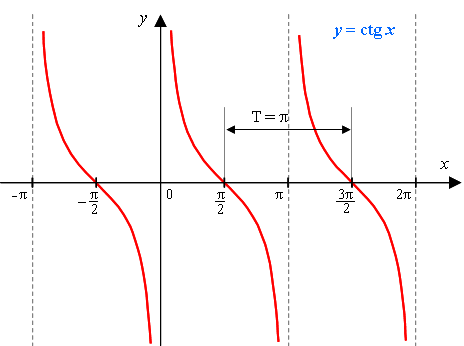
Котангенсом называется соотношение  .
Областью определения функции ctg(x) является  вся числовая прямая, кроме точек   - в этих точках функция не определена, так как, по определению  , а в точках  . А на ноль делить нельзя. Область значений лежит в промежутке (-∞;+∞).
Функция ctg(x) периодична, период Т = П. Прямые   

---

являются асимптотами. На каждом из промежутков   функция убывает. График функции ctg(x) называют котангенсоидой.  Котангенсоида пересекает ось ОХ в точках  .

1.7.Разложение в ряд

Определение тригонометрических функций через ряды.

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенных рядов:

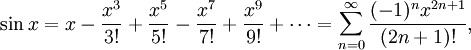
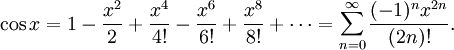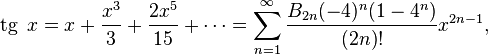
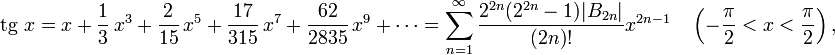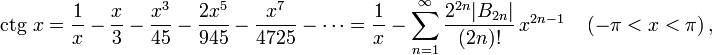
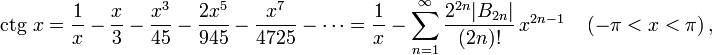Пользуясь этими формулами, а также уравнениями     можно найти разложения в ряд и других тригонометрических функций:

.



где - числа Бернулли.
1.8. Основные формулы тригонометрии

Основные тригонометрические тождества

sin² α + cos² α = 1

tg α · ctg α = 1

tg α = sin α ÷ cos α

ctg α = cos α ÷ sin α

1 + tg² α = 1 ÷ cos² α

1 + ctg² α = 1 ÷ sin² α
Формулы сложения

sin (α + β) = sin α · cos β + sin β · cos α

sin (α - β) = sin α · cos β - sin β · cos α

cos (α + β) = cos α · cos β - sin α · sin β

cos (α - β) = cos α · cos β + sin α · sin β

tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)

tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)

ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)

ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)

---

Формулы двойного угла

cos 2α = cos² α - sin² α

cos 2α = 2cos² α - 1

cos 2α = 1 - 2sin² α

sin 2α = 2sin α · cos α

tg 2α = (2tg α) ÷ (1 - tg² α)

ctg 2α = (ctg² α - 1) ÷ (2ctg α)

Формулы тройного угла

sin 3α = 3sin α - 4sin³ α

cos 3α = 4cos³ α - 3cos α

tg 3α = (3tg α - tg³ α) ÷ (1 - 3tg² α)

ctg 3α = (3ctg α - ctg³ α) ÷ (1 - 3ctg² α)

Формулы понижения степени

sin² α = (1 - cos 2α) ÷ 2

sin³ α = (3sin α - sin 3α) ÷ 4

cos² α = (1 + cos 2α) ÷ 2

cos³ α = (3cos α + cos 3α) ÷ 4

sin² α · cos² α = (1 - cos 4α) ÷ 8

sin³ α · cos³ α = (3sin 2α - sin 6α) ÷ 32

Переход от произведения к сумме

sin α · cos β = ½ (sin (α + β) + sin (α - β))

sin α · sin β = ½ (cos (α - β) - cos (α + β))

cos α · cos β = ½ (cos (α - β) + cos (α + β))

Переход от суммы к произведению

---