Файл: Задача 1 Для ступенчатого стального стержня находящегося под воздействием заданных внешних сил.docx
Добавлен: 10.11.2023
Просмотров: 357
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 1
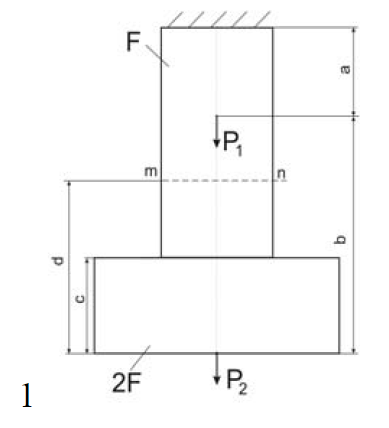
Для ступенчатого стального стержня находящегося под воздействием заданных внешних сил
1. Построить эпюры продольных сил и нормальных напряжений по длине стержня.
2. Определить перемещение свободного конца стержня и сечения m-n, приняв Е= 2⋅105 МПа.
3. Определить запас прочности стержня, приняв σТ =240 МПа.
Примечание: если запас прочности стержня получится меньше единицы, то необходимо подобрать новую площадь поперечного сечения при [σ]=160 МПа.
| Р1 (кН) | Р2 (кН) | F (см2) | a(м) | b(м) | c(м) | d (м) |
| 20 | 65 | 12 | 4,8 | 8 | 2,6 | 6 |
Решение:
1. Построение эпюры продольных сил
Определяем продольные силы на каждом участке, используя метод сечений. Мысленно разбиваем стержень на участки. Границами участков являются сечения, в которых приложены внешние силы, и место изменения размеров поперечного сечения и т.д. Таким образом, заданный стержень имеет три участка.
Чтобы не определять в заданной схеме опорную реакцию – реакцию заделки, расчет будем вести от свободного края к заделке. Величина продольной силы у заделки даст величину и направление реакции. Характерные сечения разбивают стержень на три участка. В нашем случае, применяя метод сечений, будем оставлять нижнюю и отбрасывать верхнюю отсеченную часть стержня.
При построении эпюры (графика) распределения продольных сил N проводим ось ординат графика параллельно оси стержня, откладываем в произвольно выбранном масштабе значения продольных сил по оси абсцисс.
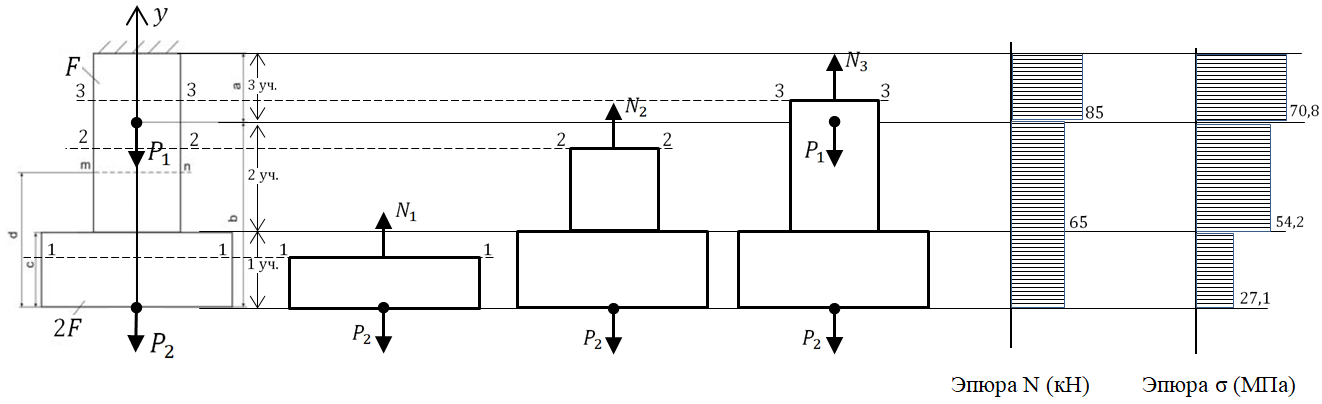
На основании метода сечений продольная сила в любом сечении стержня численно равна алгебраической сумме проекций сил (активных и реактивных) на
продольную ось стержня, действующих на оставленную часть.
При суммировании силы, направленные от сечения и вызывающие деформацию растяжения, берутся со знаком плюс, а направленные к сечению (сжатие) – со знаком минус.
Суммируя внешние силы со стороны свободного конца стержня, определим продольные силы на каждом участке:
Проведем произвольное сечение 1 – 1 на 1-м участке, отбрасываем верхнюю часть до сечения, изображаем продольную силу в сечении (вдоль оси стержня) и составляем уравнение равновесия оставленной части:
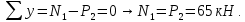
Для построения эпюры нормальных напряжений воспользуемся формулой:
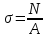
где N – продольная сила на участке, Н;
А – площадь поперечного сечения на участке, м2.
Тогда для первого участка:
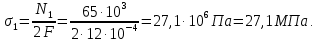
На втором участке, уравнение статики для данной системы сил имеет вид:
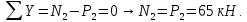
На втором участке также происходит деформация растяжения.
Определяем нормальные напряжения, возникающие в стержне на втором участке:
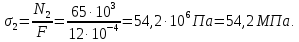
На третьем участке, уравнение статики для системы сил будет иметь вид:
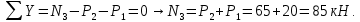
На третьем участке тоже происходит деформация растяжения.
Нормальные напряжения, возникающие в стержне на третьем участке:
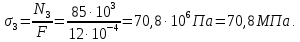
Строим эпюры продольных сил и нормальных напряжений всех участков бруса. Так как в пределах одного или нескольких смежных участков продольная сила не меняется, то эпюра ограничена прямыми, параллельными оси ординат.
Штриховка эпюр должна быть перпендикулярна оси стержня. Каждая линия штриховки (абсцисса графика) в соответствующем масштабе выражает величину продольной силы в лежащем против нее поперечном сечении стержня.
Для определения перемещения свободного конца стержня и сечения m - n воспользуемся законом Гука:
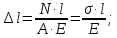
где Δl – абсолютное удлинение или укорочение (изменение длины) участка стержня, м;
N – продольная сила на участке, Н;
l – длина участка стержня, м;
E – модуль продольной упругости, Н/м2;
F – площадь поперечного сечения участка, м2;
EF – жесткость сечения бруса при растяжении (сжатии).
Перемещение свободного конца бруса равно удлинению всего стержня:
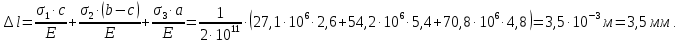
Перемещение сечения m – n равно удлинению участка длиной [a + (b − d)]:
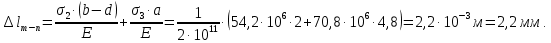
Коэффициентом запаса прочности называют отношение предельного напряжения к наибольшему расчетному напряжению:
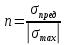
Для нашего стержня σпред = σТ = 240 МПа, σmax = σ3 = 70,8 МПа,
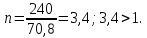
Коэффициент запаса прочности больше единицы, поэтому подбирать новую площадь поперечного сечения не требуется.
Задача 2
Для заданного стального стержня без учёта собственного веса
1. Раскрыть статическую неопределимость, построить эпюры продольных сил и нормальных напряжений по длине стержня.
2. Определить и показать на наиболее напряжённом участке нормальное и касательное напряжения в наклонном сечении (Р = 100 кН, F = 15 см2 , а = 1 м, α =15).
Проверить прочность конструкции, если [σ ]=160 МПа.
Примечание: при вычерчивании расчетной схемы утолщенные и утоненные участки стержня показывать в соответствии со значениями F1 и F2.
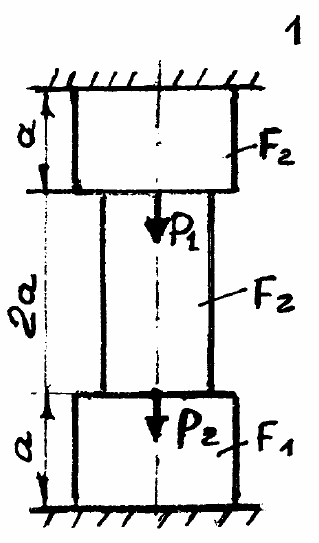
Н
 а рисунке надо полагать ошибка
а рисунке надо полагать ошибка в
| Pi | Fi | ||
| P1 | P2 | F1 | F2 |
| P | 2P | F | 2F |
Решение:
Статика дает лишь одно уравнение равновесия, так как система сил, направлена по одной прямой.
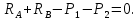
Для составления уравнения перемещений отбросим нижнюю заделку, и заменим ее действие на стержень соответствующей силой реакции RА. В результате получим стержень, защемленный одним концом (статически определимый стержень) и нагруженный, заданными силами Р1 и Р2, и неизвестной силой Y = RА.
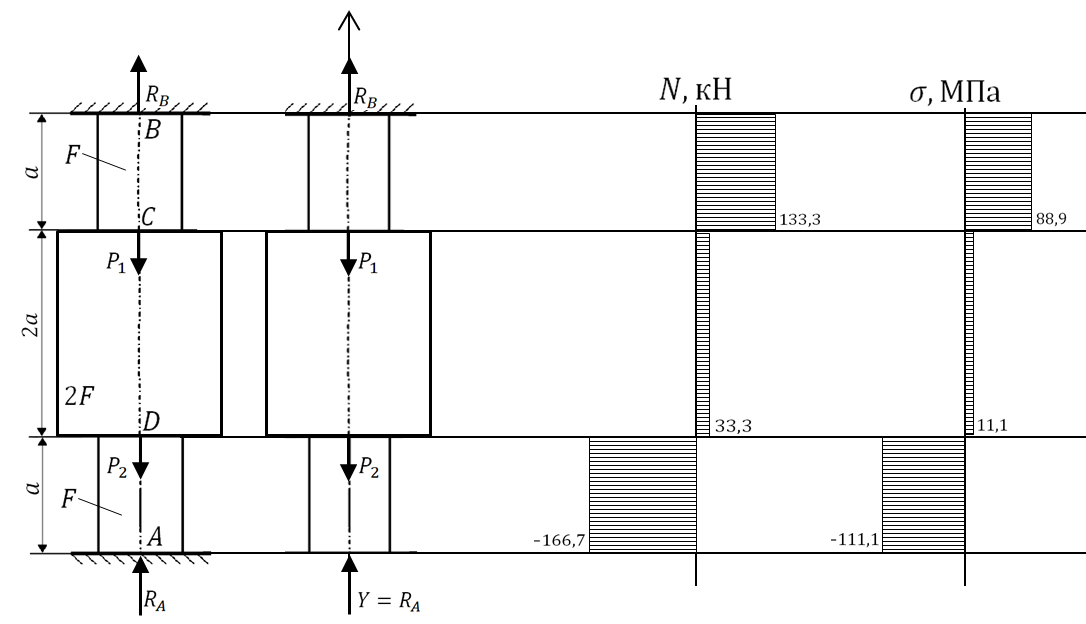
Перемещение сечения А данного стержня равно нулю, так как фактически (в заданном стержне) это сечение жестко заделано:
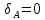
где А – суммарное перемещение сечения А, от действия всех сил: P1, P2, и Y.
Применив принцип независимости действия сил, определяем перемещение сечения А от каждой силы в отдельности, предполагая, что действует она одна, и соответствующая ей реакция опоры А, а остальные силы в это время отсутствуют. Тогда перемещение от совместного действия всех сил равно алгебраической сумме перемещений от действия каждой силы в отдельности:
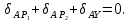
Удлинение участка ВС в результате действия силы Р1:
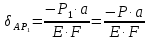
Сумма удлинений участков ВС и CD в результате действия силы Р2:
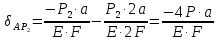
Cуммa укорочений участков AD, DC и CB в результате действия силы Y:
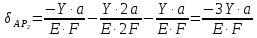
Тогда:
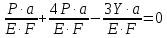
Откуда
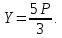
Таким образом, получаем:
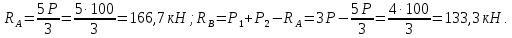
Определим продольные силы на участках стержня, начиная с нижнего
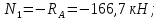
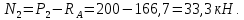
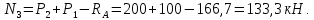
Напряжения равны продольной силе, деленной на площадь
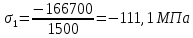
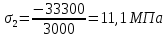
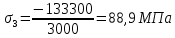
Строим эпюры по найденным значениям.
Полное напряжение, возникающее в некоторой наклонной площадке, составляющей угол α с плоскостью нормального сечения, определяется следующим образом: р = σ⋅соsα .
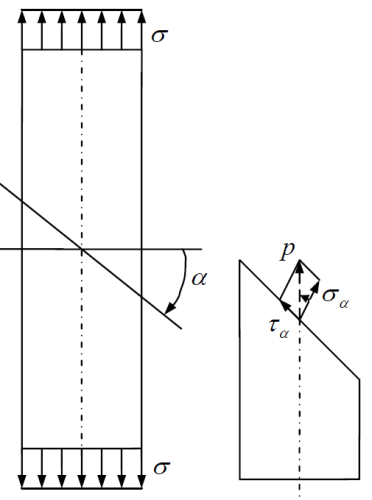
Раскладываем это напряжение по нормали и касательной к наклонной площадке, находим:
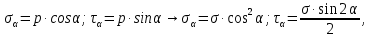
где σα и τα – нормальное и касательное напряжения в наклонном сечении.
Наибольшие напряжения возникают на участке AD, где происходит деформация сжатия:
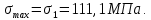
Определим на этом участке нормальное и касательное напряжения в наклонном сечении при α = 15:
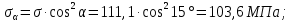
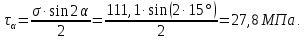
Условие прочности имеет вид:
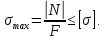
где σmax и N – соответственно нормальное напряжение и продольная сила в опасном поперечном сечении (то есть сечении, в котором возникают наибольшие напряжения);
F – площадь поперечного сечения;
[σ ] – допускаемое напряжение: [σ ]= 160 МПа ;
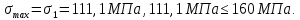
Следовательно, условие прочности выполняется и конструкция работоспособна.
Задача 3
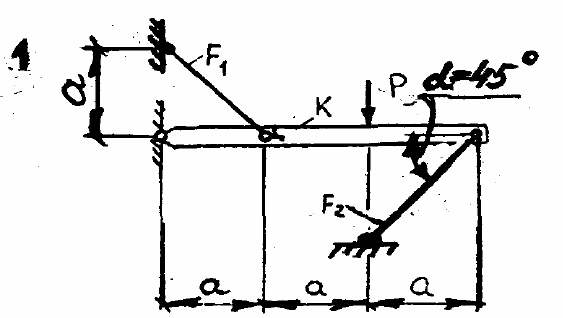
Для заданной стержневой системы
1. Раскрыть статическую неопределимость
2. Из условия прочности подобрать диаметр стальных стержней, удерживающих в равновесии абсолютно жёсткий брус К, если σпред = σТ, считая, что площадь F стержней одинакова (Р = 10 кН, а = 1 м). Запас прочности n = 2,5.
| P | Материал стержня, сталь марки | Предел текучести т, МПа |
| 2P | 20 | 250 |